
Rushbrooke inequality
Encyclopedia
In statistical mechanics
, the Rushbrooke inequality relates the critical exponent
s of a magnetic system which exhibits a first-order phase transition
in the thermodynamic limit
for non-zero temperature
T.
Since the Helmholtz free energy
is extensive, the normalization to free energy per site is given as

The magnetization M per site in the thermodynamic limit
, depending on the external magnetic field
H and temperature T is given by
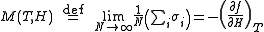
where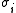 is the spin at the i-th site, and the magnetic susceptibility
is the spin at the i-th site, and the magnetic susceptibility
and specific heat at constant temperature and field are given by, respectively

and
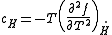
 and
and 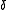 are defined in terms of the behaviour of the order parameters and response functions near the critical point as follows
are defined in terms of the behaviour of the order parameters and response functions near the critical point as follows
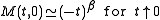

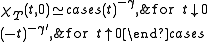
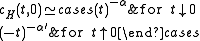
where
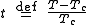
measures the temperature relative to the critical point
.
for the response functions, the relation

follows, and with thermodynamic stability requiring that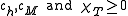 , one has
, one has
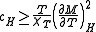
which, under the conditions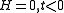 and the definition of the critical exponents gives
and the definition of the critical exponents gives
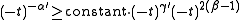
which gives the Rushbrooke inequality
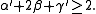
Remarkably, in experiment and in exactly solved models, the inequality actually holds as an equality.
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, the Rushbrooke inequality relates the critical exponent
Critical exponent
Critical exponents describe the behaviour of physical quantities near continuous phase transitions. It is believed, though not proven, that they are universal, i.e...
s of a magnetic system which exhibits a first-order phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
in the thermodynamic limit
Thermodynamic limit
In thermodynamics, particularly statistical mechanics, the thermodynamic limit is reached as the number of particles in a system, N, approaches infinity...
for non-zero temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
T.
Since the Helmholtz free energy
Helmholtz free energy
In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature and volume...
is extensive, the normalization to free energy per site is given as

The magnetization M per site in the thermodynamic limit
Thermodynamic limit
In thermodynamics, particularly statistical mechanics, the thermodynamic limit is reached as the number of particles in a system, N, approaches infinity...
, depending on the external magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
H and temperature T is given by
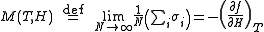
where
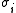 is the spin at the i-th site, and the magnetic susceptibility
is the spin at the i-th site, and the magnetic susceptibilityMagnetic susceptibility
In electromagnetism, the magnetic susceptibility \chi_m is a dimensionless proportionality constant that indicates the degree of magnetization of a material in response to an applied magnetic field...
and specific heat at constant temperature and field are given by, respectively

and
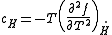
Definitions
The critical exponents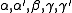 and
and  are defined in terms of the behaviour of the order parameters and response functions near the critical point as follows
are defined in terms of the behaviour of the order parameters and response functions near the critical point as follows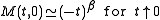

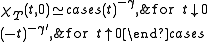
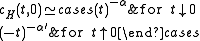
where
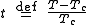
measures the temperature relative to the critical point
Critical point (thermodynamics)
In physical chemistry, thermodynamics, chemistry and condensed matter physics, a critical point, also called a critical state, specifies the conditions at which a phase boundary ceases to exist...
.
Derivation
For the magnetic analogue of the Maxwell relationsMaxwell relations
Maxwell's relations are a set of equations in thermodynamics which are derivable from the definitions of the thermodynamic potentials. The Maxwell relations are statements of equality among the second derivatives of the thermodynamic potentials. They follow directly from the fact that the order of...
for the response functions, the relation

follows, and with thermodynamic stability requiring that
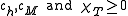 , one has
, one has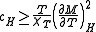
which, under the conditions
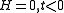 and the definition of the critical exponents gives
and the definition of the critical exponents gives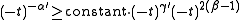
which gives the Rushbrooke inequality
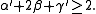
Remarkably, in experiment and in exactly solved models, the inequality actually holds as an equality.

