Russell's paradox
Encyclopedia
In the foundations of mathematics
, Russell's paradox (also known as Russell's antinomy), discovered by Bertrand Russell
in 1901, showed that the naive set theory
created by Georg Cantor
leads to a contradiction. The same paradox had been discovered a year before by Ernst Zermelo
but he did not publish the idea, which remained known only to Hilbert
, Husserl
and other members of the University of Göttingen.
According to naive set theory, any definable collection is a set. Let R be the set of all sets that are not members of themselves. If R qualifies as a member of itself, it would contradict its own definition as a set containing all sets that are not members of themselves. On the other hand, if such a set is not a member of itself, it would qualify as a member of itself by the same definition. This contradiction is Russell's paradox. Symbolically:
In 1908, two ways of avoiding the paradox were proposed, Russell's type theory
and the Zermelo set theory
, the first constructed axiomatic set theory. Zermelo's axioms went well beyond Frege's axioms of extensionality
and unlimited set abstraction, and evolved into the now-canonical Zermelo–Fraenkel set theory
(ZF).
Now we consider the set of all normal sets, R. Attempting to determine whether R is normal or abnormal is impossible: If R were a normal set, it would be contained in the set of normal sets (itself), and therefore be abnormal; and if it were abnormal, it would not be contained in the set of all normal sets (itself), and therefore be normal. This leads to the conclusion that R is neither normal nor abnormal: Russell's paradox.
with a binary predicate
, and the following as axiom
s:
for all expressions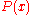 
with just 
free
Substitute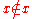
for 
. Then by existential instantiation and universal instantiation
we have
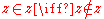
a contradiction. Therefore NST is inconsistent.
proposed an axiomatization
of set theory that avoided the paradoxes of naive set theory by replacing arbitrary set comprehension with weaker existence axioms, such as his axiom of separation (Aussonderung). Modifications to this axiomatic theory proposed in the 1920s by Abraham Fraenkel, Thoralf Skolem
, and by Zermelo himself resulted in the axiomatic set theory called ZFC. This theory became widely accepted once Zermelo's axiom of choice ceased to be controversial, and ZFC has remained the canonical axiomatic set theory down to the present day.
ZFC does not assume that, for every property, there is a set of all things satisfying that property. Rather, it asserts that given any set X, any subset of X definable using first-order logic
exists. The object R discussed above cannot be constructed in this fashion, and is therefore not a ZFC set. In some extensions of ZFC, objects like R are called proper classes. ZFC is silent about types, although some argue that Zermelo's axioms tacitly presuppose a background type theory.
In ZFC, given a set A, it is possible to define a set B that consists of exactly the sets in A that are not members of themselves. B cannot be in A by the same reasoning in Russell's Paradox. This variation of Russell's paradox shows that no set contains everything.
Through the work of Zermelo and others, especially John von Neumann
, the structure of what some see as the "natural" objects described by ZFC eventually became clear; they are the elements of the von Neumann universe
, V, built up from the empty set
by transfinitely iterating the power set operation. It is thus now possible again to reason about sets in a non-axiomatic fashion without running afoul of Russell's paradox, namely by reasoning about the elements of V. Whether it is appropriate to think of sets in this way is a point of contention among the rival points of view on the philosophy of mathematics
.
Other resolutions to Russell's paradox, more in the spirit of type theory
, include the axiomatic set theories New Foundations
and Scott-Potter set theory.
of the paradox in Frege's 1879 Begriffsschrift
and framed the problem in terms of both logic and set theory, and in particular in terms of Frege's definition of function
; in the following, p. 17 refers to a page in the original Begriffsschrift, and page 23 refers to the same page in van Heijenoort 1967:
Russell would go to cover it at length in his 1903 The Principles of Mathematics
where he repeats his first encounter with the paradox:
Russell wrote to Frege about the paradox just as Frege was preparing the second volume of his Grundgesetze der Arithmetik. Frege did not waste time responding to Russell, his letter dated 22 June 1902 appears, with van Heijenoort's commentary in Heijenoort 1967:126–127. Frege then wrote an appendix admitting to the paradox, and proposed a solution that Russell would endorse in his Principles of Mathematics, but was later considered by some unsatisfactory. For his part, Russell had his work at the printers and he added an appendix on the doctrine of types
.
For his part, Ernst Zermelo
in his (1908) A new proof of the possibility of a well-ordering (published at the same time he published "the first axiomatic set theory") laid claim to prior discovery of the antinomy
in Cantor's naive set theory. He states: "And yet, even the elementary form that Russell9 gave to the set-theoretic antinomies could have persuaded them [J. König, Jourdain, F. Bernstein] that the solution of these difficulties is not to be sought in the surrender of well-ordering but only in a suitable restriction of the notion of set". Footnote 9 is where he stakes his claim:
A written account of Zermelo's actual argument was discovered in the Nachlass of Edmund Husserl
.
It is also known that unpublished discussions of set theoretical paradoxes took place in the mathematical community at the turn of the century. van Heijenoort in his commentary before Russell's 1902 Letter to Frege states that Zermelo "had discovered the paradox independently of Russell and communicated it to Hilbert, among others, prior to its publication by Russell".
In 1923, Ludwig Wittgenstein
proposed to "dispose" of Russell's paradox as follows:
Russell and Alfred North Whitehead
wrote their three-volume Principia Mathematica
(PM) hoping to achieve what Frege had been unable to do. They sought to banish the paradoxes of naive set theory
by employing a theory of types
they devised for this purpose. While they succeeded in grounding arithmetic in a fashion, it is not at all evident that they did so by purely logical means. While PM avoided the known paradoxes and allows the derivation of a great deal of mathematics, its system gave rise to new problems.
In any event, Kurt Gödel
in 1930–31 proved that while the logic of much of PM, now known as first-order logic
, is complete
, Peano arithmetic
is necessarily incomplete if it is consistent. This is very widely – though not universally – regarded as having shown the logicist program of Frege to be impossible to complete.
supposes a barber who shaves all men who do not shave themselves and only men who do not shave themselves. When one thinks about whether the barber should shave himself or not, the paradox begins to emerge.
As another example, consider five lists of encyclopedia
entries within the same encyclopedia:
If the "List of all lists that do not contain themselves" contains itself, then it does not belong to itself and should be removed. However, if it does not list itself, then it should be added to itself.
While appealing, these layman
's versions of the paradox share a drawback: an easy refutation of the Barber paradox seems to be that such a barber does not exist, or at least does not shave (a variant of which is that the barber is a woman). The whole point of Russell's paradox is that the answer "such a set does not exist" means the definition of the notion of set within a given theory is unsatisfactory. Note the difference between the statements "such a set does not exist" and "it is an empty set
". It is like saying, "There is no bucket", or "The bucket is empty".
A notable exception to the above may be the Grelling–Nelson paradox, in which words and meaning are the elements of the scenario rather than people and hair-cutting. Though it is easy to refute the Barber's paradox by saying that such a barber does not (and cannot) exist, it is impossible to say something similar about a meaningfully defined word.
One way that the paradox has been dramatised is as follows:
Suppose that every public library has to compile a catalog of all its books. The catalog is itself one of the library's books, but while some librarians include it in the catalog for completeness, others leave it out, as being self-evident.
Now imagine that all these catalogs are sent to the national library. Some of them include themselves in their listings, others do not. The national librarian compiles two master catalogs – one of all the catalogs that list themselves, and one of all those that don't.
The question is now, should these catalogs list themselves? The 'Catalog of all catalogs that list themselves' is no problem. If the librarian doesn't include it in its own listing, it is still a true catalog of those catalogs that do include themselves. If he does include it, it remains a true catalog of those that list themselves.
However, just as the librarian cannot go wrong with the first master catalog, he is doomed to fail with the second. When it comes to the 'Catalog of all catalogs that don't list themselves', the librarian cannot include it in its own listing, because then it would belong in the other catalog, that of catalogs that do include themselves. However, if the librarian leaves it out, the catalog is incomplete. Either way, it can never be a true catalog of catalogs that do not list themselves.
Form the sentence:
Sometimes the "all" is replaced by "allers".
An example would be "paint":
or "elect"
Paradoxes that fall in this scheme include:
Foundations of mathematics
Foundations of mathematics is a term sometimes used for certain fields of mathematics, such as mathematical logic, axiomatic set theory, proof theory, model theory, type theory and recursion theory...
, Russell's paradox (also known as Russell's antinomy), discovered by Bertrand Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
in 1901, showed that the naive set theory
Naive set theory
Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
created by Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
leads to a contradiction. The same paradox had been discovered a year before by Ernst Zermelo
Ernst Zermelo
Ernst Friedrich Ferdinand Zermelo was a German mathematician, whose work has major implications for the foundations of mathematics and hence on philosophy. He is known for his role in developing Zermelo–Fraenkel axiomatic set theory and his proof of the well-ordering theorem.-Life:He graduated...
but he did not publish the idea, which remained known only to Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
, Husserl
Edmund Husserl
Edmund Gustav Albrecht Husserl was a philosopher and mathematician and the founder of the 20th century philosophical school of phenomenology. He broke with the positivist orientation of the science and philosophy of his day, yet he elaborated critiques of historicism and of psychologism in logic...
and other members of the University of Göttingen.
According to naive set theory, any definable collection is a set. Let R be the set of all sets that are not members of themselves. If R qualifies as a member of itself, it would contradict its own definition as a set containing all sets that are not members of themselves. On the other hand, if such a set is not a member of itself, it would qualify as a member of itself by the same definition. This contradiction is Russell's paradox. Symbolically:
In 1908, two ways of avoiding the paradox were proposed, Russell's type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
and the Zermelo set theory
Zermelo set theory
Zermelo set theory, as set out in an important paper in 1908 by Ernst Zermelo, is the ancestor of modern set theory. It bears certain differences from its descendants, which are not always understood, and are frequently misquoted...
, the first constructed axiomatic set theory. Zermelo's axioms went well beyond Frege's axioms of extensionality
Axiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
and unlimited set abstraction, and evolved into the now-canonical Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
(ZF).
Informal presentation
Let us call a set "abnormal" if it is a member of itself, and "normal" otherwise. For example, take the set of all squares. That set is not itself a square, and therefore is not a member of the set of all squares. So it is "normal". On the other hand, if we take the complementary set that contains all non-squares, that set is itself not a square and so should be one of its own members. It is "abnormal".Now we consider the set of all normal sets, R. Attempting to determine whether R is normal or abnormal is impossible: If R were a normal set, it would be contained in the set of normal sets (itself), and therefore be abnormal; and if it were abnormal, it would not be contained in the set of all normal sets (itself), and therefore be normal. This leads to the conclusion that R is neither normal nor abnormal: Russell's paradox.
Formal presentation
Define Naive Set Theory (NST) as the theory of predicate logicPredicate logic
In mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
with a binary predicate
, and the following as axiomAxiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s:
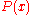for all expressions with just freeSubstitute
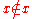for . Then by existential instantiation and universal instantiationUniversal instantiation
In logic universal instantiation is an inference from a truth about each member of a class of individuals to the truth about a particular individual of that class. It is generally given as a quantification rule for the universal quantifier but it can also be encoded in an axiom...
we have
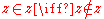
a contradiction. Therefore NST is inconsistent.
Set-theoretic responses
In 1908, Ernst ZermeloErnst Zermelo
Ernst Friedrich Ferdinand Zermelo was a German mathematician, whose work has major implications for the foundations of mathematics and hence on philosophy. He is known for his role in developing Zermelo–Fraenkel axiomatic set theory and his proof of the well-ordering theorem.-Life:He graduated...
proposed an axiomatization
Axiomatic system
In mathematics, an axiomatic system is any set of axioms from which some or all axioms can be used in conjunction to logically derive theorems. A mathematical theory consists of an axiomatic system and all its derived theorems...
of set theory that avoided the paradoxes of naive set theory by replacing arbitrary set comprehension with weaker existence axioms, such as his axiom of separation (Aussonderung). Modifications to this axiomatic theory proposed in the 1920s by Abraham Fraenkel, Thoralf Skolem
Thoralf Skolem
Thoralf Albert Skolem was a Norwegian mathematician known mainly for his work on mathematical logic and set theory.-Life:...
, and by Zermelo himself resulted in the axiomatic set theory called ZFC. This theory became widely accepted once Zermelo's axiom of choice ceased to be controversial, and ZFC has remained the canonical axiomatic set theory down to the present day.
ZFC does not assume that, for every property, there is a set of all things satisfying that property. Rather, it asserts that given any set X, any subset of X definable using first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
exists. The object R discussed above cannot be constructed in this fashion, and is therefore not a ZFC set. In some extensions of ZFC, objects like R are called proper classes. ZFC is silent about types, although some argue that Zermelo's axioms tacitly presuppose a background type theory.
In ZFC, given a set A, it is possible to define a set B that consists of exactly the sets in A that are not members of themselves. B cannot be in A by the same reasoning in Russell's Paradox. This variation of Russell's paradox shows that no set contains everything.
Through the work of Zermelo and others, especially John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
, the structure of what some see as the "natural" objects described by ZFC eventually became clear; they are the elements of the von Neumann universe
Von Neumann universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
, V, built up from the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
by transfinitely iterating the power set operation. It is thus now possible again to reason about sets in a non-axiomatic fashion without running afoul of Russell's paradox, namely by reasoning about the elements of V. Whether it is appropriate to think of sets in this way is a point of contention among the rival points of view on the philosophy of mathematics
Philosophy of mathematics
The philosophy of mathematics is the branch of philosophy that studies the philosophical assumptions, foundations, and implications of mathematics. The aim of the philosophy of mathematics is to provide an account of the nature and methodology of mathematics and to understand the place of...
.
Other resolutions to Russell's paradox, more in the spirit of type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
, include the axiomatic set theories New Foundations
New Foundations
In mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...
and Scott-Potter set theory.
History
Russell discovered the paradox in May or June 1901. By his own admission in his 1919 Introduction to Mathematical Philosophy, he "attempted to discover some flaw in Cantor's proof that there is no greatest cardinal". In a 1902 letter, he announced the discovery to Gottlob FregeGottlob Frege
Friedrich Ludwig Gottlob Frege was a German mathematician, logician and philosopher. He is considered to be one of the founders of modern logic, and made major contributions to the foundations of mathematics. He is generally considered to be the father of analytic philosophy, for his writings on...
of the paradox in Frege's 1879 Begriffsschrift
Begriffsschrift
Begriffsschrift is a book on logic by Gottlob Frege, published in 1879, and the formal system set out in that book...
and framed the problem in terms of both logic and set theory, and in particular in terms of Frege's definition of function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
; in the following, p. 17 refers to a page in the original Begriffsschrift, and page 23 refers to the same page in van Heijenoort 1967:
Russell would go to cover it at length in his 1903 The Principles of Mathematics
The Principles of Mathematics
The Principles of Mathematics is a book written by Bertrand Russell in 1903. In it he presented his famous paradox and argued his thesis that mathematics and logic are identical....
where he repeats his first encounter with the paradox:
Russell wrote to Frege about the paradox just as Frege was preparing the second volume of his Grundgesetze der Arithmetik. Frege did not waste time responding to Russell, his letter dated 22 June 1902 appears, with van Heijenoort's commentary in Heijenoort 1967:126–127. Frege then wrote an appendix admitting to the paradox, and proposed a solution that Russell would endorse in his Principles of Mathematics, but was later considered by some unsatisfactory. For his part, Russell had his work at the printers and he added an appendix on the doctrine of types
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
.
For his part, Ernst Zermelo
Ernst Zermelo
Ernst Friedrich Ferdinand Zermelo was a German mathematician, whose work has major implications for the foundations of mathematics and hence on philosophy. He is known for his role in developing Zermelo–Fraenkel axiomatic set theory and his proof of the well-ordering theorem.-Life:He graduated...
in his (1908) A new proof of the possibility of a well-ordering (published at the same time he published "the first axiomatic set theory") laid claim to prior discovery of the antinomy
Antinomy
Antinomy literally means the mutual incompatibility, real or apparent, of two laws. It is a term used in logic and epistemology....
in Cantor's naive set theory. He states: "And yet, even the elementary form that Russell9 gave to the set-theoretic antinomies could have persuaded them [J. König, Jourdain, F. Bernstein] that the solution of these difficulties is not to be sought in the surrender of well-ordering but only in a suitable restriction of the notion of set". Footnote 9 is where he stakes his claim:
A written account of Zermelo's actual argument was discovered in the Nachlass of Edmund Husserl
Edmund Husserl
Edmund Gustav Albrecht Husserl was a philosopher and mathematician and the founder of the 20th century philosophical school of phenomenology. He broke with the positivist orientation of the science and philosophy of his day, yet he elaborated critiques of historicism and of psychologism in logic...
.
It is also known that unpublished discussions of set theoretical paradoxes took place in the mathematical community at the turn of the century. van Heijenoort in his commentary before Russell's 1902 Letter to Frege states that Zermelo "had discovered the paradox independently of Russell and communicated it to Hilbert, among others, prior to its publication by Russell".
In 1923, Ludwig Wittgenstein
Ludwig Wittgenstein
Ludwig Josef Johann Wittgenstein was an Austrian philosopher who worked primarily in logic, the philosophy of mathematics, the philosophy of mind, and the philosophy of language. He was professor in philosophy at the University of Cambridge from 1939 until 1947...
proposed to "dispose" of Russell's paradox as follows:
The reason why a function cannot be its own argument is that the sign for a function already contains the prototype of its argument, and it
cannot contain itself. For let us suppose that the function F(fx) could be its own argument: in that case there would be a proposition 'F(F(fx))', in which the outer function F and the inner function F must have different meanings, since the inner one has the form O(f(x)) and the outer one has the form Y(O(fx)). Only the letter 'F' is common to the two functions, but the letter by itself signifies nothing. This immediately becomes clear if instead of 'F(Fu)' we write '(do) : F(Ou) . Ou = Fu'. That disposes of Russell's paradox. (Tractatus Logico-PhilosophicusTractatus Logico-PhilosophicusThe Tractatus Logico-Philosophicus is the only book-length philosophical work published by the Austrian philosopher Ludwig Wittgenstein in his lifetime. It was an ambitious project: to identify the relationship between language and reality and to define the limits of science...
, 3.333)
Russell and Alfred North Whitehead
Alfred North Whitehead
Alfred North Whitehead, OM FRS was an English mathematician who became a philosopher. He wrote on algebra, logic, foundations of mathematics, philosophy of science, physics, metaphysics, and education...
wrote their three-volume Principia Mathematica
Principia Mathematica
The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...
(PM) hoping to achieve what Frege had been unable to do. They sought to banish the paradoxes of naive set theory
Naive set theory
Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
by employing a theory of types
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
they devised for this purpose. While they succeeded in grounding arithmetic in a fashion, it is not at all evident that they did so by purely logical means. While PM avoided the known paradoxes and allows the derivation of a great deal of mathematics, its system gave rise to new problems.
In any event, Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
in 1930–31 proved that while the logic of much of PM, now known as first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, is complete
Gödel's completeness theorem
Gödel's completeness theorem is a fundamental theorem in mathematical logic that establishes a correspondence between semantic truth and syntactic provability in first-order logic. It was first proved by Kurt Gödel in 1929....
, Peano arithmetic
Peano axioms
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
is necessarily incomplete if it is consistent. This is very widely – though not universally – regarded as having shown the logicist program of Frege to be impossible to complete.
Applied versions
There are some versions of this paradox that are closer to real-life situations and may be easier to understand for non-logicians. For example, the Barber paradoxBarber paradox
The Barber paradox is a puzzle derived from Russell's paradox. It was used by Bertrand Russell himself as an illustration of the paradox, though he attributes it to an unnamed person who suggested it to him. It shows that an apparently plausible scenario is logically impossible.- The Paradox...
supposes a barber who shaves all men who do not shave themselves and only men who do not shave themselves. When one thinks about whether the barber should shave himself or not, the paradox begins to emerge.
As another example, consider five lists of encyclopedia
Encyclopedia
An encyclopedia is a type of reference work, a compendium holding a summary of information from either all branches of knowledge or a particular branch of knowledge....
entries within the same encyclopedia:
List of articles about people:
|
List of articles starting with the letter L:
...
... |
List of articles about places:
|
List of articles about Japan:
|
List of all lists that do not contain themselves:
...
...
|
If the "List of all lists that do not contain themselves" contains itself, then it does not belong to itself and should be removed. However, if it does not list itself, then it should be added to itself.
While appealing, these layman
Layman
A layperson or layman is a person who is not an expert in a given field of knowledge. The term originally meant a member of the laity, i.e. a non-clergymen, but over the centuries shifted in definition....
's versions of the paradox share a drawback: an easy refutation of the Barber paradox seems to be that such a barber does not exist, or at least does not shave (a variant of which is that the barber is a woman). The whole point of Russell's paradox is that the answer "such a set does not exist" means the definition of the notion of set within a given theory is unsatisfactory. Note the difference between the statements "such a set does not exist" and "it is an empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
". It is like saying, "There is no bucket", or "The bucket is empty".
A notable exception to the above may be the Grelling–Nelson paradox, in which words and meaning are the elements of the scenario rather than people and hair-cutting. Though it is easy to refute the Barber's paradox by saying that such a barber does not (and cannot) exist, it is impossible to say something similar about a meaningfully defined word.
One way that the paradox has been dramatised is as follows:
Suppose that every public library has to compile a catalog of all its books. The catalog is itself one of the library's books, but while some librarians include it in the catalog for completeness, others leave it out, as being self-evident.
Now imagine that all these catalogs are sent to the national library. Some of them include themselves in their listings, others do not. The national librarian compiles two master catalogs – one of all the catalogs that list themselves, and one of all those that don't.
The question is now, should these catalogs list themselves? The 'Catalog of all catalogs that list themselves' is no problem. If the librarian doesn't include it in its own listing, it is still a true catalog of those catalogs that do include themselves. If he does include it, it remains a true catalog of those that list themselves.
However, just as the librarian cannot go wrong with the first master catalog, he is doomed to fail with the second. When it comes to the 'Catalog of all catalogs that don't list themselves', the librarian cannot include it in its own listing, because then it would belong in the other catalog, that of catalogs that do include themselves. However, if the librarian leaves it out, the catalog is incomplete. Either way, it can never be a true catalog of catalogs that do not list themselves.
Russell-like paradoxes
As illustrated above for the Barber paradox, Russell's paradox is not hard to extend. Take:- A transitive verbTransitive verbIn syntax, a transitive verb is a verb that requires both a direct subject and one or more objects. The term is used to contrast intransitive verbs, which do not have objects.-Examples:Some examples of sentences with transitive verbs:...
, that can be applied to its substantive form.
Form the sentence:
- The
er that s all (and only those) who don't themselves,
Sometimes the "all" is replaced by "all
An example would be "paint":
- The painter that paints all (and only those) that don't paint themselves.
or "elect"
- The elector (representativeGroup representationIn the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
), that elects all that don't elect themselves.
Paradoxes that fall in this scheme include:
- The barber with "shave"Barber paradoxThe Barber paradox is a puzzle derived from Russell's paradox. It was used by Bertrand Russell himself as an illustration of the paradox, though he attributes it to an unnamed person who suggested it to him. It shows that an apparently plausible scenario is logically impossible.- The Paradox...
. - The original Russell's paradox with "contain": The container (Set) that contains all (containers) that don't contain themselves.
- The Grelling–Nelson paradox with "describer": The describer (word) that describes all words, that don't describe themselves.
- Richard's paradoxRichard's paradoxIn logic, Richard's paradox is a semantical antinomy in set theory and natural language first described by the French mathematician Jules Richard in 1905. Today, the paradox is ordinarily used in order to motivate the importance of carefully distinguishing between mathematics and metamathematics...
with "denote": The denoter (number) that denotes all denoters (numbers) that don't denote themselves. (In this paradox, all descriptions of numbers get an assigned number. The term "that denotes all denoters (numbers) that don't denote themselves" is here called Richardian.)
Related paradoxes
- The liar paradoxLiar paradoxIn philosophy and logic, the liar paradox or liar's paradox , is the statement "this sentence is false"...
and Epimenides paradoxEpimenides paradoxThe Epimenides paradox is a problem in logic. It is named after the Cretan philosopher Epimenides of Knossos , There is no single statement of the problem; a typical variation is given in the book Gödel, Escher, Bach, by Douglas Hofstadter:...
, whose origins are ancient - The Kleene–Rosser paradox, showing that the original lambda calculusLambda calculusIn mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
is inconsistent, by means of a self-negating statement - Curry's paradoxCurry's paradoxCurry's paradox is a paradox that occurs in naive set theory or naive logics, and allows the derivation of an arbitrary sentence from a self-referring sentence and some apparently innocuous logical deduction rules...
(named after Haskell CurryHaskell CurryHaskell Brooks Curry was an American mathematician and logician. Curry is best known for his work in combinatory logic; while the initial concept of combinatory logic was based on a single paper by Moses Schönfinkel, much of the development was done by Curry. Curry is also known for Curry's...
), which does not require negationNegationIn logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified... - The smallest uninteresting integerInteresting number paradoxThe interesting number paradox is a semi-humorous paradox that arises from attempting to classify natural numbers as "interesting" or "dull". The paradox states that all natural numbers are interesting...
paradox
See also
- Self-referenceSelf-referenceSelf-reference occurs in natural or formal languages when a sentence or formula refers to itself. The reference may be expressed either directly—through some intermediate sentence or formula—or by means of some encoding...
- Universal setUniversal setIn set theory, a universal set is a set which contains all objects, including itself. In set theory as usually formulated, the conception of a set of all sets leads to a paradox...
- On DenotingOn Denoting"On Denoting", written by Bertrand Russell, is one of the most significant and influential philosophical essays of the 20th century. It was published in the philosophy journal Mind in 1905; then reprinted, in both a special 2005 anniversary issue of the same journal and in Russell's Logic and...
, one of Russell's first attempts at critiquing Frege
External links
- Russell's Paradox at Cut-the-KnotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
: "Russell's Paradox" – by A. D. Irvine.