.gif)
SO(8)
Encyclopedia
In mathematics
, SO(8) is the special orthogonal group acting on eight-dimensional Euclidean space
. It could be either a real or complex simple Lie group
of rank 4 and dimension 28.
SO(8) is not simply connected, having a fundamental group
isomorphic to Z2
. The universal cover of SO(8) is the spin group Spin(8).
(as for all SO(2n) for 
), while the center of Spin(8) is Z2×Z2 (as for all Spin(4n), 
).
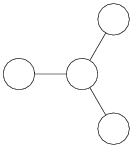SO(8) is unique among the simple Lie group
s in that its Dynkin diagram (shown right) (D4 under the Dynkin classification) possesses a three-fold symmetry
. This gives rise to peculiar feature of Spin(8) known as triality
. Related to this is the fact that the two spinor
representations
, as well as the fundamental
vector representation, of Spin(8) are all eight-dimensional (for all other spin groups the spinor representation is either smaller or larger than the vector representation). The triality automorphism
of Spin(8) lives in the outer automorphism group
of Spin(8) which is isomorphic to the symmetric group
S3 that permutes these three representations. The automorphism group acts on the center Z2 x Z2 (which also has automorphism group isomorphic to
which may also be considered as the general linear group
over the finite field with two elements,
). When one quotients Spin(8) by one central Z2, breaking this symmetry and obtaining SO(8), the remaining outer automorphism group
is only Z2. The triality symmetry acts again on the further quotient SO(8)/Z2.
Sometimes Spin(8) appears naturally in an "enlarged" form, as the automorphism group of Spin(8), which breaks up as a semidirect product
:
.
Root system
Cartan matrix
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, SO(8) is the special orthogonal group acting on eight-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. It could be either a real or complex simple Lie group
Simple Lie group
In group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
of rank 4 and dimension 28.
Spin(8)
Like all special orthogonal groups of SO(8) is not simply connected, having a fundamental groupFundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
isomorphic to Z2
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
. The universal cover of SO(8) is the spin group Spin(8).
Center
The center of SO(8) is Z2, the diagonal matrices (as for all SO(2n) for ), while the center of Spin(8) is Z2×Z2 (as for all Spin(4n), ).Triality
Simple Lie group
In group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
s in that its Dynkin diagram (shown right) (D4 under the Dynkin classification) possesses a three-fold symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
. This gives rise to peculiar feature of Spin(8) known as triality
Triality
In mathematics, triality is a relationship between three vector spaces, analogous to the duality relation between dual vector spaces. Most commonly, it describes those special features of the Dynkin diagram D4 and the associated Lie group Spin, the double cover of 8-dimensional rotation group SO,...
. Related to this is the fact that the two spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
representations
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
, as well as the fundamental
Fundamental representation
In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
vector representation, of Spin(8) are all eight-dimensional (for all other spin groups the spinor representation is either smaller or larger than the vector representation). The triality automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of Spin(8) lives in the outer automorphism group
Outer automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
of Spin(8) which is isomorphic to the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
S3 that permutes these three representations. The automorphism group acts on the center Z2 x Z2 (which also has automorphism group isomorphic to
which may also be considered as the general linear groupGeneral linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
over the finite field with two elements,
). When one quotients Spin(8) by one central Z2, breaking this symmetry and obtaining SO(8), the remaining outer automorphism groupOuter automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
is only Z2. The triality symmetry acts again on the further quotient SO(8)/Z2.
Sometimes Spin(8) appears naturally in an "enlarged" form, as the automorphism group of Spin(8), which breaks up as a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
:
.Root systemRoot systemIn mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
Cartan matrixCartan matrixIn mathematics, the term Cartan matrix has three meanings. All of these are named after the French mathematician Élie Cartan. In fact, Cartan matrices in the context of Lie algebras were first investigated by Wilhelm Killing, whereas the Killing form is due to Cartan.- Lie algebras :A generalized...