Sarkovskii's theorem
Encyclopedia
In mathematics
, Sharkovskii's theorem, named after Oleksandr Mikolaiovich Sharkovsky
, is a result about discrete dynamical systems. One of the implications of the theorem is that if a continuous discrete dynamical system on the real line
has a periodic point
of period 3, then it must have periodic points of every other period.
is a continuous function
. We say that the number x is a periodic point of period m if f m(x) = x (where f m denotes the composition of m copies of f
) and having least period m if furthermore f k(x) ≠ x for all 0 < k < m. We are interested in the possible periods of periodic points of f. Consider the following ordering
of the positive integer
s:
We start, that is, with the odd numbers in increasing order, then 2 times the odds, 4 times the odds, 8 times the odds, etc., and at the end we put the powers of two in decreasing order. Every positive integer appears exactly once somewhere on this list. Sharkovskii's theorem states that if f has a periodic point of least period m and m precedes n in the above ordering, then f has also a periodic point of least period n.
As a consequence, we see that if f has only finitely many periodic points, then they must all have periods which are powers of two. Furthermore, if there is a periodic point of period three, then there are periodic points of all other periods.
Sharkovskii's theorem does not state that there are stable cycles of those periods, just that there are cycles of those periods. For systems such as the logistic map
, the bifurcation diagram
shows a range of parameter values for which apparently the only cycle has period 3. In fact, there must be cycles of all periods there, but they are not stable and therefore not visible on the computer generated picture.
Interestingly, the above "Sharkovskii ordering" of the positive integers also occurs in a slightly different context in connection with the logistic map: the stable cycles appear in this order in the bifurcation diagram, starting with 1 and ending with 3, as the parameter is increased. (Here we ignore a stable cycle if a stable cycle of the same order has occurred earlier.)
The assumption of continuity is important, as the discontinuous function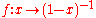
, for which every value has period 3, would otherwise be a counterexample.
with periodic points of period 3 only: take a rotation by 120 degrees, for example. But some generalizations are possible, typically involving the mapping class group of the space minus a periodic orbit.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Sharkovskii's theorem, named after Oleksandr Mikolaiovich Sharkovsky
Oleksandr Mikolaiovich Sharkovsky
Oleksandr Mikolaiovich Sharkovsky is a prominent Ukrainian mathematician most famous for developing Sharkovsky's Theorem in 1964. In 2006 he became a member of the National Academy of Sciences of Ukraine.-External links:...
, is a result about discrete dynamical systems. One of the implications of the theorem is that if a continuous discrete dynamical system on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
has a periodic point
Periodic point
In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time.- Iterated functions :...
of period 3, then it must have periodic points of every other period.
The theorem
Suppose- f : R → R
is a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. We say that the number x is a periodic point of period m if f m(x) = x (where f m denotes the composition of m copies of f
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
) and having least period m if furthermore f k(x) ≠ x for all 0 < k < m. We are interested in the possible periods of periodic points of f. Consider the following ordering
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
of the positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s:
We start, that is, with the odd numbers in increasing order, then 2 times the odds, 4 times the odds, 8 times the odds, etc., and at the end we put the powers of two in decreasing order. Every positive integer appears exactly once somewhere on this list. Sharkovskii's theorem states that if f has a periodic point of least period m and m precedes n in the above ordering, then f has also a periodic point of least period n.
As a consequence, we see that if f has only finitely many periodic points, then they must all have periods which are powers of two. Furthermore, if there is a periodic point of period three, then there are periodic points of all other periods.
Sharkovskii's theorem does not state that there are stable cycles of those periods, just that there are cycles of those periods. For systems such as the logistic map
Logistic map
The logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
, the bifurcation diagram
Bifurcation diagram
In mathematics, particularly in dynamical systems, a bifurcation diagram shows the possible long-term values of a system as a function of a bifurcation parameter in the system...
shows a range of parameter values for which apparently the only cycle has period 3. In fact, there must be cycles of all periods there, but they are not stable and therefore not visible on the computer generated picture.
Interestingly, the above "Sharkovskii ordering" of the positive integers also occurs in a slightly different context in connection with the logistic map: the stable cycles appear in this order in the bifurcation diagram, starting with 1 and ending with 3, as the parameter is increased. (Here we ignore a stable cycle if a stable cycle of the same order has occurred earlier.)
The assumption of continuity is important, as the discontinuous function
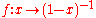, for which every value has period 3, would otherwise be a counterexample.Generalizations
Sharkovskii's theorem does not immediately apply to dynamical systems on other topological spaces. It is easy to find a circle mapCircle map
In mathematics, a circle map is a member of a family of dynamical systems on the circle first defined by Andrey Kolmogorov. Kolmogorov proposed this family as a simplified model for driven mechanical rotors . The circle map equations also describe a simplified model of the phase-locked loop in...
with periodic points of period 3 only: take a rotation by 120 degrees, for example. But some generalizations are possible, typically involving the mapping class group of the space minus a periodic orbit.
External link
- Keith Burns and Boris Hasselblatt, The Sharkovsky theorem: a natural direct proof