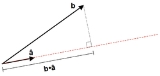
Scalar resolute
Encyclopedia
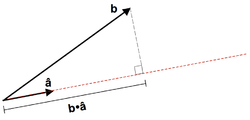
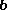 in the direction of a vector
in the direction of a vector  (or scalar projection of
(or scalar projection of  on
on  ) is given by:
) is given by: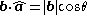
where the operator
 denotes a dot product
denotes a dot productDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
,
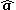 is the unit vector in the direction of
is the unit vector in the direction of  ,
, 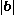 is the length of
is the length of 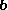 , and
, and 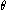 is the angle
is the angleAngle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
between
 and
and 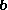 .
.For an intuitive understanding of this formula, recall from trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
that
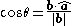 and simply rearrange the terms by multiplying both sides by
and simply rearrange the terms by multiplying both sides by  .
.The scalar projection is a scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
, and is the length of the orthogonal projection of the vector
 onto the vector
onto the vector  , with a minus sign if the direction is opposite.
, with a minus sign if the direction is opposite.Multiplying the scalar projection by
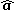 converts it into the vector projection, a vector.
converts it into the vector projection, a vector.

