
Scale relativity
Encyclopedia
Scale relativity is a theory of space-time initially developed by Laurent Nottale
, working at the French observatory of Meudon, near Paris. It is an extension of the concept of relativity
found the special relativity
and general relativity
to physical scale
s (time, length, energy, or momentum scales). If scales in nature are always relative, an absolute scale cannot exist. As a consequence, fundamental physical laws need to be scale invariant. While differential
trajectories found in standard physics are automatically scale invariant, it is the main insight of the theory that also certain non-differential trajectories (which explicitly depend on the scale of the observer) can be scale invariant and new tools are developed to treat such trajectories. It is one of the main successes of the theory that the laws of quantum mechanics
, like the Schroedinger equation, can be derived directly from the assumption that space-time itself is non-differential and scale invariant. Scale invariance
is closely related to the self-similarity
observed in fractals.
of this object will appear very fast; if on the other hand we look up to the sky and follow the movement of a jumbo-jet we sometimes wonder why it doesn't fall down, because from this distance it appears to be almost standing still.
Is this a pure subjective perception? The passengers in the jet will say that the clouds rushing by prove that the plane is moving fast, whereas the earth below is nearly standing still. And if the 'object' under the microscope were an ant that just woke up from coma, it would observe itself moving - relatively to the surface it is bounded to - with merely a few centimeters per minute.
This is reminiscent of the situation where one walks inside a train. Oneself observes walking rather slow, while an observer outside will add the velocity
of the train to the walking speed, and say that the person inside the train is walking fast relatively to the ground. A similar observation led Galileo to formulate a relativity principle of motion. Likewise the former observations led Nottale to formulate scale relativity.

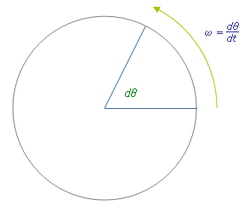 While Galilean relativity of motion can be expressed by differences:
While Galilean relativity of motion can be expressed by differences:

The relativity of scales can be expressed by ratios:
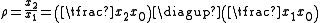
This can be derived by taking the Perspective (visual)
in account, which is the phenomena that as objects become more distant, they appear smaller, because their angular diameter (visual angle) decreases. Then an observer on the ground sees v ' as the tangential velocity v (observed inside the plane) scaled down by the ratio of r'/r , that's between radius r (distance to the observed movement) and r ' (distance to the projective plane, e.g. 'the window').
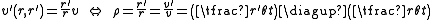
The last term follows from (*)
Now the difference between a jet flying in a circle from its own perspecitve , i.e. a rotation that our intuition would favor as a real movement, and a perspectively projected rotation conceived by a far away observer, is that
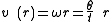 (*)
(*)
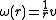
That is a jet flying through your garden (small r) will have a much higher angular velocity, than one that is 'hanging' in the sky.
Now what if r goes to zero? Then the angular velocity would become infinite for any non-zero
v > 0 (ultraviolet catastrophe
). This is the analog to infinite speed in Galilean Relativity, when one rides on a train that is riding on a train, ... ad infinitum. This leads to (Lorentzian) scale relativity that is analogous to special relativity.
: just like a constant speed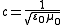 in Maxwell's equations
in Maxwell's equations
, which does not appear to depend on the speed of the observer, suggests that the law of combination of speeds must preserve this invariant, similarly, the appearance of a constant length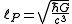 in Schrödinger's equation suggests that the law of combination of scales must preserve this invariant. In other words, just like
in Schrödinger's equation suggests that the law of combination of scales must preserve this invariant. In other words, just like  is a physical speed limit,
is a physical speed limit, 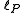 is a physical length limit.
is a physical length limit.
s, both in cosmology and at small scale, including:
Laurent Nottale
Laurent Nottale is an astrophysicist, a director of research at CNRS, and a researcher at the Paris Observatory. He is the author and inventor of the theory of Scale Relativity which aims to unify quantum physics and relativity theory....
, working at the French observatory of Meudon, near Paris. It is an extension of the concept of relativity
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
found the special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
and general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
to physical scale
Scale (spatial)
Spatial scale provides a "shorthand" form for discussing relative lengths, areas, distances and sizes. A microclimate, for instance, is one which might occur in a mountain valley or near a lakeshore, whereas a megatrend is one which involves the whole planet....
s (time, length, energy, or momentum scales). If scales in nature are always relative, an absolute scale cannot exist. As a consequence, fundamental physical laws need to be scale invariant. While differential
Differential
-Mathematics:* Differential comprises multiple related meanings of the word, both in calculus and differential geometry, such as an infinitesimal change in the value of a function* Differential algebra* Differential calculus...
trajectories found in standard physics are automatically scale invariant, it is the main insight of the theory that also certain non-differential trajectories (which explicitly depend on the scale of the observer) can be scale invariant and new tools are developed to treat such trajectories. It is one of the main successes of the theory that the laws of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, like the Schroedinger equation, can be derived directly from the assumption that space-time itself is non-differential and scale invariant. Scale invariance
Scale invariance
In physics and mathematics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor...
is closely related to the self-similarity
Self-similarity
In mathematics, a self-similar object is exactly or approximately similar to a part of itself . Many objects in the real world, such as coastlines, are statistically self-similar: parts of them show the same statistical properties at many scales...
observed in fractals.
Observation and motivation
Two everyday observations are, that if we look at an object at a very small distance, say through a microscope, then even the slightest movementMotion (physics)
In physics, motion is a change in position of an object with respect to time. Change in action is the result of an unbalanced force. Motion is typically described in terms of velocity, acceleration, displacement and time . An object's velocity cannot change unless it is acted upon by a force, as...
of this object will appear very fast; if on the other hand we look up to the sky and follow the movement of a jumbo-jet we sometimes wonder why it doesn't fall down, because from this distance it appears to be almost standing still.
Is this a pure subjective perception? The passengers in the jet will say that the clouds rushing by prove that the plane is moving fast, whereas the earth below is nearly standing still. And if the 'object' under the microscope were an ant that just woke up from coma, it would observe itself moving - relatively to the surface it is bounded to - with merely a few centimeters per minute.
This is reminiscent of the situation where one walks inside a train. Oneself observes walking rather slow, while an observer outside will add the velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of the train to the walking speed, and say that the person inside the train is walking fast relatively to the ground. A similar observation led Galileo to formulate a relativity principle of motion. Likewise the former observations led Nottale to formulate scale relativity.
Mathematical formulation



The relativity of scales can be expressed by ratios:
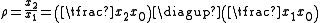
This can be derived by taking the Perspective (visual)
Perspective (visual)
Perspective, in context of vision and visual perception, is the way in which objects appear to the eye based on their spatial attributes; or their dimensions and the position of the eye relative to the objects...
in account, which is the phenomena that as objects become more distant, they appear smaller, because their angular diameter (visual angle) decreases. Then an observer on the ground sees v ' as the tangential velocity v (observed inside the plane) scaled down by the ratio of r'/r , that's between radius r (distance to the observed movement) and r ' (distance to the projective plane, e.g. 'the window').
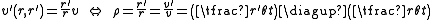
The last term follows from (*)
Now the difference between a jet flying in a circle from its own perspecitve , i.e. a rotation that our intuition would favor as a real movement, and a perspectively projected rotation conceived by a far away observer, is that
- in the real case the angular velocityAngular velocityIn physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
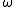 is constant, while the tangential velocity depends on the radius
is constant, while the tangential velocity depends on the radius
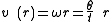 (*)
(*)
- in the projective case the tangential velocity v (the speed the passengers observe) is constant, while here the angular velocity (a.k.a angular frequencyAngular frequencyIn physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
) depends reciprocal on radius r
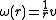
That is a jet flying through your garden (small r) will have a much higher angular velocity, than one that is 'hanging' in the sky.
Now what if r goes to zero? Then the angular velocity would become infinite for any non-zero
v > 0 (ultraviolet catastrophe
Ultraviolet catastrophe
The ultraviolet catastrophe, also called the Rayleigh–Jeans catastrophe, was a prediction of late 19th century/early 20th century classical physics that an ideal black body at thermal equilibrium will emit radiation with infinite power....
). This is the analog to infinite speed in Galilean Relativity, when one rides on a train that is riding on a train, ... ad infinitum. This leads to (Lorentzian) scale relativity that is analogous to special relativity.
(Lorentzian) Scale Relativity principle
The scale relativity extends to scales the reasoning made by Einstein on speeds in special relativitySpecial relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
: just like a constant speed
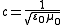 in Maxwell's equations
in Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, which does not appear to depend on the speed of the observer, suggests that the law of combination of speeds must preserve this invariant, similarly, the appearance of a constant length
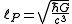 in Schrödinger's equation suggests that the law of combination of scales must preserve this invariant. In other words, just like
in Schrödinger's equation suggests that the law of combination of scales must preserve this invariant. In other words, just like  is a physical speed limit,
is a physical speed limit, 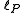 is a physical length limit.
is a physical length limit.Predictions and retrodictions
Scale relativity made a number of true predictions, as well as a number of retrodictionRetrodiction
Retrodiction is the act of making a "prediction" about the past. This is especially useful when one wishes to test a theory whose actual predictions are too long-term to be of immediate use...
s, both in cosmology and at small scale, including:
- Prediction of the location of exoplanets http://luth2.obspm.fr/~luthier/nottale/ukresult.htm
- Explanation of some observed large-scale structures http://luth2.obspm.fr/~luthier/nottale/DaRochaNottaleL.pdf
- Relation between mass and charge of the electron http://luth2.obspm.fr/~luthier/nottale/ukmachar.htm
See also
- Causal dynamical triangulation
- Conformal groupConformal groupIn mathematics, the conformal group is the group of transformations from a space to itself that preserve all angles within the space. More formally, it is the group of transformations that preserve the conformal geometry of the space. Several specific conformal groups are particularly important:*...
- Doubly special relativity
- Fractal cosmologyFractal cosmologyIn physical cosmology, fractal cosmology is a set of minority cosmological theories which state that the distribution of matter in the Universe, or the structure of the universe itself, is a fractal. More generally, it relates to the usage or appearance of fractals in the study of the universe and...
- Fractals
- Olbers' paradoxOlbers' paradoxIn astrophysics and physical cosmology, Olbers' paradox is the argument that the darkness of the night sky conflicts with the assumption of an infinite and eternal static universe. It is one of the pieces of evidence for a non-static universe such as the current Big Bang model. The argument is also...
- Perspective (graphical)Perspective (graphical)Perspective in the graphic arts, such as drawing, is an approximate representation, on a flat surface , of an image as it is seen by the eye...
- Scale invarianceScale invarianceIn physics and mathematics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor...

