
Schauder estimates
Encyclopedia
In mathematics
, the Schauder estimates are a collection of results due to concerning the regularity of solutions to linear, uniformly elliptic
partial differential equation
s. The estimates say that when the equation has appropriately smooth terms and appropriately smooth solutions, then the Hölder norm
of the solution can be controlled in terms of the Hölder norms for the coefficient and source terms. Since these estimates do not assume the existence of the solution, they are called a priori estimate
s.
There is both an interior result, giving a Hölder condition for the solution in interior domains away from the boundary, and a boundary result, giving the Hölder condition for the solution in the entire domain. The former bound depends only on the spatial dimension, the equation, and the distance to the boundary; the latter depends on the smoothness of the boundary as well.
The Schauder estimates are a necessary precondition to using the method of continuity
to proving the existence and regularity of solutions to the Dirichlet problem
for elliptic PDEs. This result says that when the coefficients of the equation and the nature of the boundary conditions are sufficiently smooth, there is a smooth classical solution to the PDE.
The supremum norm of a continuous function is given by
is given by
For a function which is Hölder continuous with exponent , that is to say,
, that is to say, 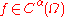 the usual Hölder seminorm
the usual Hölder seminorm
is given by

The sum of the two is the full Hölder norm of f
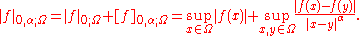
For differentiable functions u, it is necessary to consider the higher order norms, involving derivatives. The norm in the space of functions with k continuous derivatives,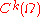 , is given by
, is given by

where ranges over all multi-indices
ranges over all multi-indices
of appropriate orders. For functions with kth order derivatives which are Holder continuous with exponent , the appropriate semi-norm is given by
, the appropriate semi-norm is given by
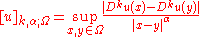
which gives a full norm of
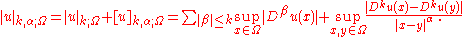
For the interior estimates, the norms are weighted by the distance to the boundary
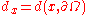
raised to the same power as the derivative, and the seminorms are weighted by
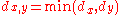
raised to the appropriate power. The resulting weighted interior norm for a function is given by
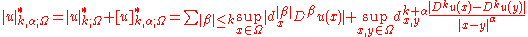
It is occasionally necessary to add "extra" powers of the weight, denoted by
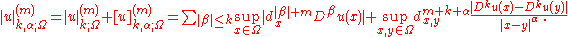
 on the domain
on the domain  to the elliptic, second order partial differential equation
to the elliptic, second order partial differential equation
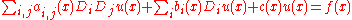
where the source term satisfies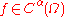 , there exists a constant
, there exists a constant 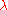 such that the
such that the  are strictly elliptic,
are strictly elliptic,
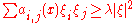 for all
for all 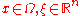
and the relevant norms coefficients are all bounded by another constant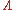
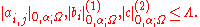
Then the weighted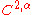 norm of u is controlled by the supremum of u and the Holder norm of f:
norm of u is controlled by the supremum of u and the Holder norm of f:
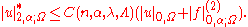
 be a
be a 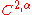 domain (that is to say, about any point on the boundary of the domain the boundary surface can be realized, after an appropriate rotation of coordinates, as a
domain (that is to say, about any point on the boundary of the domain the boundary surface can be realized, after an appropriate rotation of coordinates, as a 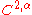 function), with Dirichlet boundary data that coincides with a function
function), with Dirichlet boundary data that coincides with a function 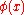 which is also at least
which is also at least 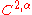 . Then subject to analogous conditions on the coefficients as in the case of the interior estimate, the unweighted Holder norm of u is controlled by the unweighted norms of the source term, the boundary data, and the supremum norm of u:
. Then subject to analogous conditions on the coefficients as in the case of the interior estimate, the unweighted Holder norm of u is controlled by the unweighted norms of the source term, the boundary data, and the supremum norm of u:

When the solution u satisfies the maximum principle
, the first term on the right hand side can be dropped.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Schauder estimates are a collection of results due to concerning the regularity of solutions to linear, uniformly elliptic
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s. The estimates say that when the equation has appropriately smooth terms and appropriately smooth solutions, then the Hölder norm
Hölder condition
In mathematics, a real or complex-valued function ƒ on d-dimensional Euclidean space satisfies a Hölder condition, or is Hölder continuous, when there are nonnegative real constants C, \alpha , such that...
of the solution can be controlled in terms of the Hölder norms for the coefficient and source terms. Since these estimates do not assume the existence of the solution, they are called a priori estimate
A priori estimate
In the theory of partial differential equations, an a priori estimate is an estimate for the size of a solution or its derivatives of a partial differential equation. A priori is Latin for "from before" and refers to the fact that the estimate for the solution is derived before the solution is...
s.
There is both an interior result, giving a Hölder condition for the solution in interior domains away from the boundary, and a boundary result, giving the Hölder condition for the solution in the entire domain. The former bound depends only on the spatial dimension, the equation, and the distance to the boundary; the latter depends on the smoothness of the boundary as well.
The Schauder estimates are a necessary precondition to using the method of continuity
Method of continuity
In the mathematics of Banach spaces, the method of continuity provides sufficient conditions for deducing the invertibility of one bounded linear operator from that of another, related operator.-Formulation:...
to proving the existence and regularity of solutions to the Dirichlet problem
Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
for elliptic PDEs. This result says that when the coefficients of the equation and the nature of the boundary conditions are sufficiently smooth, there is a smooth classical solution to the PDE.
Notation
The Schauder estimates are given in terms of weighted Hölder norms; the notation will follow that given in the text of .The supremum norm of a continuous function
 is given by
is given by
For a function which is Hölder continuous with exponent
 , that is to say,
, that is to say, 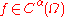 the usual Hölder seminorm
the usual Hölder seminormHölder condition
In mathematics, a real or complex-valued function ƒ on d-dimensional Euclidean space satisfies a Hölder condition, or is Hölder continuous, when there are nonnegative real constants C, \alpha , such that...
is given by

The sum of the two is the full Hölder norm of f
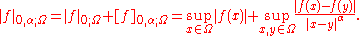
For differentiable functions u, it is necessary to consider the higher order norms, involving derivatives. The norm in the space of functions with k continuous derivatives,
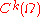 , is given by
, is given by
where
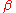 ranges over all multi-indices
ranges over all multi-indicesMulti-index notation
The mathematical notation of multi-indices simplifies formulae used in multivariable calculus, partial differential equations and the theory of distributions, by generalising the concept of an integer index to an ordered tuple of indices....
of appropriate orders. For functions with kth order derivatives which are Holder continuous with exponent
 , the appropriate semi-norm is given by
, the appropriate semi-norm is given by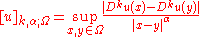
which gives a full norm of
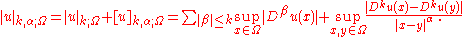
For the interior estimates, the norms are weighted by the distance to the boundary
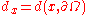
raised to the same power as the derivative, and the seminorms are weighted by
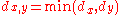
raised to the appropriate power. The resulting weighted interior norm for a function is given by
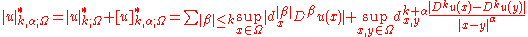
It is occasionally necessary to add "extra" powers of the weight, denoted by
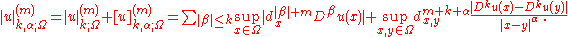
Formulation
The formulations in this section are taken from the text of .Interior estimates
Consider a bounded solution on the domain
on the domain  to the elliptic, second order partial differential equation
to the elliptic, second order partial differential equation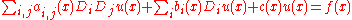
where the source term satisfies
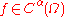 , there exists a constant
, there exists a constant 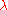 such that the
such that the  are strictly elliptic,
are strictly elliptic,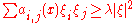 for all
for all 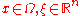
and the relevant norms coefficients are all bounded by another constant
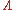
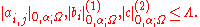
Then the weighted
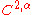 norm of u is controlled by the supremum of u and the Holder norm of f:
norm of u is controlled by the supremum of u and the Holder norm of f: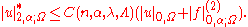
Boundary estimates
Let be a
be a 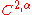 domain (that is to say, about any point on the boundary of the domain the boundary surface can be realized, after an appropriate rotation of coordinates, as a
domain (that is to say, about any point on the boundary of the domain the boundary surface can be realized, after an appropriate rotation of coordinates, as a 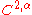 function), with Dirichlet boundary data that coincides with a function
function), with Dirichlet boundary data that coincides with a function 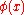 which is also at least
which is also at least 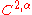 . Then subject to analogous conditions on the coefficients as in the case of the interior estimate, the unweighted Holder norm of u is controlled by the unweighted norms of the source term, the boundary data, and the supremum norm of u:
. Then subject to analogous conditions on the coefficients as in the case of the interior estimate, the unweighted Holder norm of u is controlled by the unweighted norms of the source term, the boundary data, and the supremum norm of u:
When the solution u satisfies the maximum principle
Maximum principle
In mathematics, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain...
, the first term on the right hand side can be dropped.

