
Schmidt number
Encyclopedia
Schmidt number is a dimensionless number defined as the ratio
of momentum diffusivity
(viscosity
) and mass diffusivity, and is used to characterize fluid
flows in which there are simultaneous momentum and mass diffusion convection processes. It was named after the German engineer Ernst Heinrich Wilhelm Schmidt (1892-1975).
Schmidt number is the ratio of the shear component for diffusivity viscosity/density to the diffusivity
for mass transfer D. It physically relates the relative thickness of the hydrodynamic layer and mass-transfer boundary layer.
It is defined as:
where:
The heat transfer analog of the Schmidt number is the Prandtl number.
s, the Schmidt number represents dimensionless specific power
.
Gustav Schmidt of the German Polytechnic Institute of Prague published an analysis in 1871 for the now-famous closed-form
solution for an idealized isothermal Stirling engine model.
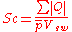
where,
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
of momentum diffusivity
Momentum diffusion
Momentum diffusion refers to the diffusion, or spread of momentum between particles of matter, usually in the liquid state....
(viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
) and mass diffusivity, and is used to characterize fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
flows in which there are simultaneous momentum and mass diffusion convection processes. It was named after the German engineer Ernst Heinrich Wilhelm Schmidt (1892-1975).
Schmidt number is the ratio of the shear component for diffusivity viscosity/density to the diffusivity
Diffusivity
Diffusivity can refer to:*Diffusivity of heat*Diffusivity of mass:** Molecular diffusivity ** Eddy diffusivity*Momentum diffusivity...
for mass transfer D. It physically relates the relative thickness of the hydrodynamic layer and mass-transfer boundary layer.
It is defined as:

where:
-
 is the kinematic viscosity or (
is the kinematic viscosity or ( /
/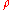 ) in units of (m2/s)
) in units of (m2/s) -
 is the mass diffusivity (m2/s).
is the mass diffusivity (m2/s). -
 is the dynamic viscosity of the fluidFluidIn physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
is the dynamic viscosity of the fluidFluidIn physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
(Pa·s or N·s/m² or kg/m·s) -
 is the densityDensityThe mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
is the densityDensityThe mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
of the fluid (kg/m³).
The heat transfer analog of the Schmidt number is the Prandtl number.
Stirling engines
For Stirling engineStirling engine
A Stirling engine is a heat engine operating by cyclic compression and expansion of air or other gas, the working fluid, at different temperature levels such that there is a net conversion of heat energy to mechanical work....
s, the Schmidt number represents dimensionless specific power
Specific power
In physics and engineering, surface power density or sometimes simply specific power is power per unit area.-Applications:* The intensity of electromagnetic radiation can be expressed in W/m2...
.
Gustav Schmidt of the German Polytechnic Institute of Prague published an analysis in 1871 for the now-famous closed-form
Closed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
solution for an idealized isothermal Stirling engine model.
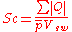
where,
-
 is the Schmidt number
is the Schmidt number -
 is the heat transferred into the working fluid
is the heat transferred into the working fluid -
 is the mean pressure of the working fluid
is the mean pressure of the working fluid -
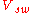 is the volume swept by the piston.
is the volume swept by the piston.

