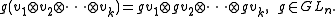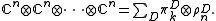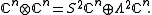Schur–Weyl duality
Encyclopedia
Schur–Weyl duality is a mathematical theorem in representation theory
that relates irreducible finite-dimensional representations of the general linear
and symmetric
groups. It is named after two pioneers of representation theory of Lie group
s, Issai Schur
, who discovered the phenomenon, and Hermann Weyl
, who popularized it in his books on quantum mechanics
and classical groups as a way of classifying representations of unitary
and general linear groups.
that determine each other. Consider the tensor
space
The symmetric group
Sk on k letters acts
on this space (on the left) by permuting the factors,
The general linear group GLn of invertible n×n matrices acts on it by the simultaneous matrix multiplication
,
These two actions commute
, and in its concrete form, the Schur–Weyl duality asserts that under the joint action of the groups Sk and GLn, the tensor space decomposes into a direct sum of tensor products of irreducible modules for these two groups that determine each other,
The summands are indexed by the Young diagrams D with k boxes and at most n rows, and representations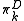
of Sk with different D are mutually non-isomorphic, and the same is true for representations 
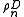of GLn.
The abstract form of the Schur–Weyl duality asserts that two algebras of operators on the tensor space generated by the actions of GLn and Sk are the full mutual centralizers in the algebra of the endomorphisms
The symmetric group S2 consists of two elements and has two irreducible representations, the trivial representation
and the sign representation. The trivial representation of S2 gives rise to the symmetric tensors, which are invariant (i.e. do not change) under the permutation of the factors, and the sign representation corresponds to the skew-symmetric tensors, which flip the sign.
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
that relates irreducible finite-dimensional representations of the general linear
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
and symmetric
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
groups. It is named after two pioneers of representation theory of Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s, Issai Schur
Issai Schur
Issai Schur was a mathematician who worked in Germany for most of his life. He studied at Berlin...
, who discovered the phenomenon, and Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
, who popularized it in his books on quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and classical groups as a way of classifying representations of unitary
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
and general linear groups.
Description
Schur–Weyl duality forms an archetypical situation in representation theory involving two kinds of symmetrySymmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
that determine each other. Consider the tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
space
-
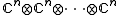with k factors.
The symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sk on k letters acts
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on this space (on the left) by permuting the factors,
The general linear group GLn of invertible n×n matrices acts on it by the simultaneous matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
,
These two actions commute
Commute
Commute, commutation or commutative may refer to:* Commuting, the process of travelling between a place of residence and a place of work* Commutative property, a property of a mathematical operation...
, and in its concrete form, the Schur–Weyl duality asserts that under the joint action of the groups Sk and GLn, the tensor space decomposes into a direct sum of tensor products of irreducible modules for these two groups that determine each other,
The summands are indexed by the Young diagrams D with k boxes and at most n rows, and representations
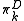of Sk with different D are mutually non-isomorphic, and the same is true for representations 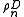of GLn.The abstract form of the Schur–Weyl duality asserts that two algebras of operators on the tensor space generated by the actions of GLn and Sk are the full mutual centralizers in the algebra of the endomorphisms
Example
Suppose that k = 2 and n is greater than one. Then the Schur–Weyl duality is the statement that the space of two-tensors decomposes into symmetric and antisymmetric parts, each of which is an irreducible module for GLn:
The symmetric group S2 consists of two elements and has two irreducible representations, the trivial representation
Trivial representation
In the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...
and the sign representation. The trivial representation of S2 gives rise to the symmetric tensors, which are invariant (i.e. do not change) under the permutation of the factors, and the sign representation corresponds to the skew-symmetric tensors, which flip the sign.