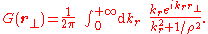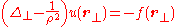Screened Poisson equation
Encyclopedia
In Physics
, the screened Poisson equation is the following partial differential equation
:
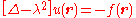
where
is the Laplace operator
, λ is a constant, f is an arbitrary function of position (known as the "source function") and u is the function to be determined. The screened Poisson equation occurs frequently in Physics
, including Yukawa's
theory of meson
s and electric field screening
in plasma
s.
In the homogenous case (f=0), the screened Poisson equation is the same as the time-independent Klein–Gordon equation. In the inhomogeneous case, the screened Poisson equation is very similar to the inhomogeneous Helmholtz equation, the only difference being the sign within the brackets.
Without loss of generality, we will take λ to be non-negative. When λ is zero
, the equation reduces to Poisson's equation
. Therefore, when λ is very small, the solution approaches that of the unscreened Poisson equation, which, in dimension
, is a superposition of 1/r functions weighted by the source function f:
On the other hand, when λ is extremely large, u approaches the value f/λ², which goes to zero as λ goes to infinity. As we shall see, the solution for intermediate values of λ behaves as a superposition of screened (or damped) 1/r functions, with λ behaving as the strength of the screening.
The screened Poisson equation can be solved for general f using the method of Green's function
s. The Green's function G is defined by
Assuming u and its derivatives vanish at large r, we may perform a continuous Fourier transform
in spatial coordinates:
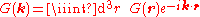
where the integral is taken over all space. It is then straightforward to show that
The Green's function in r is therefore given by the inverse Fourier transform,
This integral may be evaluated using spherical coordinates
in k-space. The integration over the angular coordinates is straightforward, and the integral reduces to one over the radial wavenumber
:
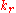This may be evaluated using contour integration
. The result is:
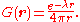
The solution to the full problem is then given by
As stated above, this is a superposition of screened 1/r functions, weighted by the source function f and with λ acting as the strength of the screening. The screened 1/r function is often encountered in physics as a screened Coulomb potential, also called a "Yukawa potential".
In two dimensions:
In the case of a magnetized plasma, the screened Poisson equation
is quasi-2D:
with
and 
, with 
the magnetic field and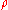 
is the (ion) Larmor radius.
The two-dimensional Fourier Transform
of the associated Green's function
is:
The 2D screened Poisson equation
yields:
The Green's function
is therefore given by the inverse Fourier transform:
This integral can be calculated using polar coordinates in k-space
:
The integration over the angular coordinate is straightforward, and the integral reduces to one over the radial wavenumber
:
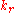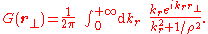
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the screened Poisson equation is the following partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
:
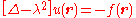
where
is the Laplace operatorLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
, λ is a constant, f is an arbitrary function of position (known as the "source function") and u is the function to be determined. The screened Poisson equation occurs frequently in Physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, including Yukawa's
Hideki Yukawa
né , was a Japanese theoretical physicist and the first Japanese Nobel laureate.-Biography:Yukawa was born in Tokyo and grew up in Kyoto. In 1929, after receiving his degree from Kyoto Imperial University, he stayed on as a lecturer for four years. After graduation, he was interested in...
theory of meson
Meson
In particle physics, mesons are subatomic particles composed of one quark and one antiquark, bound together by the strong interaction. Because mesons are composed of sub-particles, they have a physical size, with a radius roughly one femtometer: 10−15 m, which is about the size of a proton...
s and electric field screening
Electric field screening
Screening is the damping of electric fields caused by the presence of mobile charge carriers. It is an important part of the behavior of charge-carrying fluids, such as ionized gases and conduction electrons in semiconductors and metals....
in plasma
Plasma (physics)
In physics and chemistry, plasma is a state of matter similar to gas in which a certain portion of the particles are ionized. Heating a gas may ionize its molecules or atoms , thus turning it into a plasma, which contains charged particles: positive ions and negative electrons or ions...
s.
In the homogenous case (f=0), the screened Poisson equation is the same as the time-independent Klein–Gordon equation. In the inhomogeneous case, the screened Poisson equation is very similar to the inhomogeneous Helmholtz equation, the only difference being the sign within the brackets.
Without loss of generality, we will take λ to be non-negative. When λ is zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
, the equation reduces to Poisson's equation
Poisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
. Therefore, when λ is very small, the solution approaches that of the unscreened Poisson equation, which, in dimension
, is a superposition of 1/r functions weighted by the source function f:On the other hand, when λ is extremely large, u approaches the value f/λ², which goes to zero as λ goes to infinity. As we shall see, the solution for intermediate values of λ behaves as a superposition of screened (or damped) 1/r functions, with λ behaving as the strength of the screening.
The screened Poisson equation can be solved for general f using the method of Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
s. The Green's function G is defined by
Assuming u and its derivatives vanish at large r, we may perform a continuous Fourier transform
Continuous Fourier transform
The Fourier transform is a mathematical operation that decomposes a function into its constituent frequencies, known as a frequency spectrum. For instance, the transform of a musical chord made up of pure notes is a mathematical representation of the amplitudes of the individual notes that make...
in spatial coordinates:
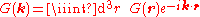
where the integral is taken over all space. It is then straightforward to show that
The Green's function in r is therefore given by the inverse Fourier transform,
This integral may be evaluated using spherical coordinates
Spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
in k-space. The integration over the angular coordinates is straightforward, and the integral reduces to one over the radial wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
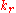:This may be evaluated using contour integration
Line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
. The result is:
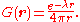
The solution to the full problem is then given by
As stated above, this is a superposition of screened 1/r functions, weighted by the source function f and with λ acting as the strength of the screening. The screened 1/r function is often encountered in physics as a screened Coulomb potential, also called a "Yukawa potential".
In two dimensions:
In the case of a magnetized plasma, the screened Poisson equation
Screened Poisson equation
In Physics, the screened Poisson equation is the following partial differential equation:\left[ \Delta - \lambda^2 \right] u = - f...
is quasi-2D:
with
and , with the magnetic field and 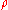is the (ion) Larmor radius.The two-dimensional Fourier Transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the associated Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
is:
The 2D screened Poisson equation
Screened Poisson equation
In Physics, the screened Poisson equation is the following partial differential equation:\left[ \Delta - \lambda^2 \right] u = - f...
yields:
-
.
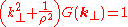The Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
is therefore given by the inverse Fourier transform:
This integral can be calculated using polar coordinates in k-space
K-space
K-space can refer to:*Another name for the Frequency domain but referring to a spatial rather than temporal frequency*Reciprocal space for the Fourier transform of a spatial function...
:
The integration over the angular coordinate is straightforward, and the integral reduces to one over the radial wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
:
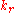