
Second class constraints
Encyclopedia
In a constrained Hamiltonian system, a dynamical quantity is second class if its Poisson bracket with at least one constraint is nonvanishing. A constraint that has a nonzero Poisson bracket with at least one other constraint, then, is a second class constraint.
See first class constraints or Dirac bracket
for the preliminaries.
Let's start with the action
describing a Newtonian
particle of mass
m constrained to a surface of radius R within a uniform gravitational field
g. When one works in Lagrangian mechanics, there are several ways to implement a constraint: one can switch to generalized coordinates that manifestly solve the constraint or one can use a Lagrange multiplier.
In this case, the particle is constrained to a sphere, therefore the natural solution would be to use angular coordinates to describe the position of the particle instead of Cartesian and solve the constraint in that way (the first choice). For didactic reasons, instead, consider the problem in Cartesian coordinates with a Lagrange multiplier term.
The action is given by
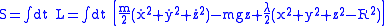
where the last term is the Lagrange multiplier term enforcing the constraint.
Of course, we could have just used different coordinates and written it as

instead, but let's look at the former coordinatization.
The conjugate momenta are given by
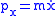 ,
, 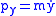 ,
, 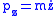 ,
, 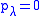 .
.
Note that we can't determine from the momenta.
from the momenta.
The Hamiltonian
is given by
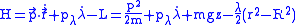 .
.
We can't eliminate at this stage yet. We are here treating
at this stage yet. We are here treating  as a shorthand for a function of the symplectic space
as a shorthand for a function of the symplectic space
which we have yet to determine and not an independent variable. For notational consistency, define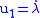 from now on. The above Hamiltonian with the
from now on. The above Hamiltonian with the 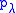 term is the "naive Hamiltonian". Note that since, on-shell, the constraint must be satisfied, one cannot distinguish between the naive Hamiltonian and the above Hamiltonian with the undetermined coefficient,
term is the "naive Hamiltonian". Note that since, on-shell, the constraint must be satisfied, one cannot distinguish between the naive Hamiltonian and the above Hamiltonian with the undetermined coefficient, 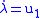 , on-shell.
, on-shell.
We have the primary constraint pλ=0.
We require, on the grounds of consistency, that the Poisson bracket
of all the constraints with the Hamiltonian vanish at the constrained subspace. In other words, the constraints must not evolve in time if they are going to be identically zero along the equations of motion.
From this consistency condition, we immediately get the secondary constraint
r2-R2=0.
By the same reasoning, this constraint should be added into the Hamiltonian with an undetermined (not necessarily constant) coefficient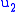 . At this point, the Hamiltonian is
. At this point, the Hamiltonian is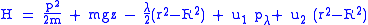
And from the secondary constraint, we get the tertiary constraint
 ,
,
by demanding on the grounds of consistency that on-shell. Again, one should add this constraint into the Hamiltonian since on-shell no one can tell the difference. Therefore, so far, the Hamiltonian looks like
on-shell. Again, one should add this constraint into the Hamiltonian since on-shell no one can tell the difference. Therefore, so far, the Hamiltonian looks like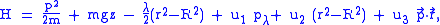
where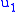 ,
, 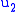 , and
, and 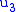 are still completely undetermined. Note that frequently all constraints that are found from consistency conditions are referred to as "secondary constraints" and secondary, tertiary, quaternary, etc. constraints are not distinguished.
are still completely undetermined. Note that frequently all constraints that are found from consistency conditions are referred to as "secondary constraints" and secondary, tertiary, quaternary, etc. constraints are not distinguished.
The tertiary constraint's consistency condition yields
This is not a quaternary constraint, but a condition which fixes one of the undetermined coefficients. In particular, it fixes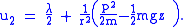
Now that there are new terms in the Hamiltonian, one should go back and check the consistency conditions for the primary and secondary constraints. The secondary constraint's consistency condition gives
Again, this is not a new constraint; it only determines that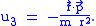
At this point there are no more constraints or consistency conditions to check.
Putting it all together, .
.
When finding the equations of motion, one should use the above Hamiltonian, and as long as one is careful to never use constraints before taking derivatives in the Poisson bracket then one gets the correct equations of motion. That is, the equations of motion are given by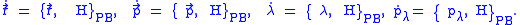
Before analyzing the Hamiltonian, consider the three constraints: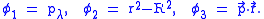
Notice the nontrivial Poisson bracket
structure of the constraints. In particular,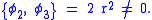
The above Poisson bracket does not just fail to vanish off-shell, which might be anticipated, but even on-shell it is nonzero. Therefore,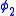 and
and 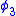 are second class constraints while
are second class constraints while 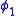 is a first class constraint
is a first class constraint
. Note that these constraints satisfy the regularity condition.
Here, we have a symplectic space where the Poisson bracket does not have "nice properties" on the constrained subspace. But Dirac
noticed that we can turn the underlying differential manifold of the symplectic space
into a Poisson manifold
using a different bracket, called the Dirac bracket
, such that the Dirac bracket of any (smooth) function with any of the second class constraints always vanishes and a couple of other nice properties.
If one wanted to canonically quantize this system, then, one needs to promote the canonical Dirac brackets not the canonical Poisson brackets to commutation relations.
Examination of the above Hamiltonian shows a number of interesting things happening. One thing to note is that on-shell when the constraints are satisfied the extended Hamiltonian is identical to the naive Hamiltonian, as required. Also, note that dropped out of the extended Hamiltonian. Since
dropped out of the extended Hamiltonian. Since 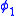 is a first class primary constraint it should be interpreted as a generator of a gauge transformation. The gauge freedom is the freedom to choose
is a first class primary constraint it should be interpreted as a generator of a gauge transformation. The gauge freedom is the freedom to choose  which has ceased to have any effect on the particle's dynamics. Therefore, that
which has ceased to have any effect on the particle's dynamics. Therefore, that  dropped out of the Hamiltonian, that
dropped out of the Hamiltonian, that 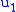 is undetermined, and that
is undetermined, and that  is first class, are all closely interrelated.
is first class, are all closely interrelated.
Note that it would be more natural not to start with a Lagrangian with a Lagrange multiplier, but instead take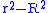 as a primary constraint and proceed through the formalism. The result would the elimination of the extraneous
as a primary constraint and proceed through the formalism. The result would the elimination of the extraneous  dynamical quantity. Perhaps, the example is more edifying in its current form.
dynamical quantity. Perhaps, the example is more edifying in its current form.
. The fields are and the action is
and the action is
where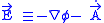
and .
.
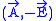 and
and 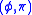 are canonical variables. The second class constraints are
are canonical variables. The second class constraints are
and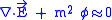 .
.
The Hamiltonian is given by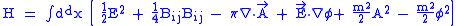 .
.
1, N. K. Falck and A. C. Hirshfeld, 1983, "Dirac-bracket quantisation of a constrained nonlinear system: the rigid rotator", Eur. J. Phys. 4 p.5. doi: 10.1088/0143-0807/4/1/003 (Tote that the form of the quantum momentum in this paper is dubious.)
2, T. Homma, T. Inamoto, and T. Miyazaki, 1990, "Schrödinger equation for the nonrelativistic particle constrained on a hypersurface in a curved space ", Phys. Rev. D 42, p.2049. http://prd.aps.org/abstract/PRD/v42/i6/p2049_1. (Tote that the Hamiltonian suggested by the authors from second form of the constraint, (i.e., the time derivative of the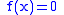 ) , is not completely compatible with the formalism of Hamiltonian mechanics.)
) , is not completely compatible with the formalism of Hamiltonian mechanics.)
See first class constraints or Dirac bracket
Dirac bracket
The Dirac bracket is a generalization of the Poisson bracket developed by Paul Dirac to correctly treat systems with second class constraints in Hamiltonian mechanics and canonical quantization. It is an important part of Dirac's development of Hamiltonian mechanics to handle more general Lagrangians...
for the preliminaries.
An example: a particle confined to a sphere
Before going on to the general theory, let's look at a specific example step by step to motivate the general analysis.Let's start with the action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
describing a Newtonian
Newtonian
Newtonian refers to the work of Isaac Newton, in particular:* Newtonian mechanics, also known as classical mechanics* Newtonian telescope, a type of reflecting telescope* Newtonian cosmology* Newtonian dynamics...
particle of mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
m constrained to a surface of radius R within a uniform gravitational field
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
g. When one works in Lagrangian mechanics, there are several ways to implement a constraint: one can switch to generalized coordinates that manifestly solve the constraint or one can use a Lagrange multiplier.
In this case, the particle is constrained to a sphere, therefore the natural solution would be to use angular coordinates to describe the position of the particle instead of Cartesian and solve the constraint in that way (the first choice). For didactic reasons, instead, consider the problem in Cartesian coordinates with a Lagrange multiplier term.
The action is given by
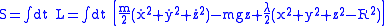
where the last term is the Lagrange multiplier term enforcing the constraint.
Of course, we could have just used different coordinates and written it as

instead, but let's look at the former coordinatization.
The conjugate momenta are given by
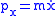 ,
, 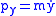 ,
, 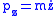 ,
, 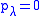 .
.Note that we can't determine
 from the momenta.
from the momenta.The Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
is given by
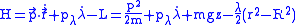 .
.We can't eliminate
 at this stage yet. We are here treating
at this stage yet. We are here treating  as a shorthand for a function of the symplectic space
as a shorthand for a function of the symplectic spaceSymplectic space
A symplectic space is either a symplectic manifold or a symplectic vector space. The latter is a special case of the former....
which we have yet to determine and not an independent variable. For notational consistency, define
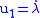 from now on. The above Hamiltonian with the
from now on. The above Hamiltonian with the 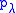 term is the "naive Hamiltonian". Note that since, on-shell, the constraint must be satisfied, one cannot distinguish between the naive Hamiltonian and the above Hamiltonian with the undetermined coefficient,
term is the "naive Hamiltonian". Note that since, on-shell, the constraint must be satisfied, one cannot distinguish between the naive Hamiltonian and the above Hamiltonian with the undetermined coefficient, 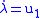 , on-shell.
, on-shell.We have the primary constraint pλ=0.
We require, on the grounds of consistency, that the Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
of all the constraints with the Hamiltonian vanish at the constrained subspace. In other words, the constraints must not evolve in time if they are going to be identically zero along the equations of motion.
From this consistency condition, we immediately get the secondary constraint
r2-R2=0.
By the same reasoning, this constraint should be added into the Hamiltonian with an undetermined (not necessarily constant) coefficient
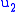 . At this point, the Hamiltonian is
. At this point, the Hamiltonian is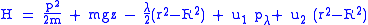
And from the secondary constraint, we get the tertiary constraint
 ,
,by demanding on the grounds of consistency that
 on-shell. Again, one should add this constraint into the Hamiltonian since on-shell no one can tell the difference. Therefore, so far, the Hamiltonian looks like
on-shell. Again, one should add this constraint into the Hamiltonian since on-shell no one can tell the difference. Therefore, so far, the Hamiltonian looks like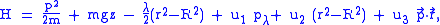
where
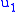 ,
, 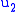 , and
, and 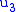 are still completely undetermined. Note that frequently all constraints that are found from consistency conditions are referred to as "secondary constraints" and secondary, tertiary, quaternary, etc. constraints are not distinguished.
are still completely undetermined. Note that frequently all constraints that are found from consistency conditions are referred to as "secondary constraints" and secondary, tertiary, quaternary, etc. constraints are not distinguished.The tertiary constraint's consistency condition yields

This is not a quaternary constraint, but a condition which fixes one of the undetermined coefficients. In particular, it fixes
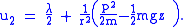
Now that there are new terms in the Hamiltonian, one should go back and check the consistency conditions for the primary and secondary constraints. The secondary constraint's consistency condition gives

Again, this is not a new constraint; it only determines that
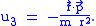
At this point there are no more constraints or consistency conditions to check.
Putting it all together,
 .
.When finding the equations of motion, one should use the above Hamiltonian, and as long as one is careful to never use constraints before taking derivatives in the Poisson bracket then one gets the correct equations of motion. That is, the equations of motion are given by
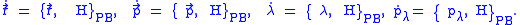
Before analyzing the Hamiltonian, consider the three constraints:
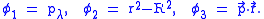
Notice the nontrivial Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
structure of the constraints. In particular,
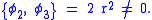
The above Poisson bracket does not just fail to vanish off-shell, which might be anticipated, but even on-shell it is nonzero. Therefore,
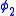 and
and 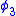 are second class constraints while
are second class constraints while 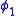 is a first class constraint
is a first class constraintFirst class constraint
In a constrained Hamiltonian system, a dynamical quantity is called a first class constraint if its Poisson bracket with all the other constraints vanishes on the constraint surface .-Poisson brackets:In Hamiltonian mechanics, consider a symplectic manifold M with a smooth Hamiltonian over...
. Note that these constraints satisfy the regularity condition.
Here, we have a symplectic space where the Poisson bracket does not have "nice properties" on the constrained subspace. But Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
noticed that we can turn the underlying differential manifold of the symplectic space
Symplectic space
A symplectic space is either a symplectic manifold or a symplectic vector space. The latter is a special case of the former....
into a Poisson manifold
Poisson manifold
In mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
using a different bracket, called the Dirac bracket
Dirac bracket
The Dirac bracket is a generalization of the Poisson bracket developed by Paul Dirac to correctly treat systems with second class constraints in Hamiltonian mechanics and canonical quantization. It is an important part of Dirac's development of Hamiltonian mechanics to handle more general Lagrangians...
, such that the Dirac bracket of any (smooth) function with any of the second class constraints always vanishes and a couple of other nice properties.
If one wanted to canonically quantize this system, then, one needs to promote the canonical Dirac brackets not the canonical Poisson brackets to commutation relations.
Examination of the above Hamiltonian shows a number of interesting things happening. One thing to note is that on-shell when the constraints are satisfied the extended Hamiltonian is identical to the naive Hamiltonian, as required. Also, note that
 dropped out of the extended Hamiltonian. Since
dropped out of the extended Hamiltonian. Since 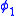 is a first class primary constraint it should be interpreted as a generator of a gauge transformation. The gauge freedom is the freedom to choose
is a first class primary constraint it should be interpreted as a generator of a gauge transformation. The gauge freedom is the freedom to choose  which has ceased to have any effect on the particle's dynamics. Therefore, that
which has ceased to have any effect on the particle's dynamics. Therefore, that  dropped out of the Hamiltonian, that
dropped out of the Hamiltonian, that 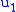 is undetermined, and that
is undetermined, and that  is first class, are all closely interrelated.
is first class, are all closely interrelated.Note that it would be more natural not to start with a Lagrangian with a Lagrange multiplier, but instead take
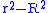 as a primary constraint and proceed through the formalism. The result would the elimination of the extraneous
as a primary constraint and proceed through the formalism. The result would the elimination of the extraneous  dynamical quantity. Perhaps, the example is more edifying in its current form.
dynamical quantity. Perhaps, the example is more edifying in its current form.Example: Proca action
Another example we will use is the Proca actionProca action
In physics, in the area of field theory, the Proca action describes a massive spin-1 field of mass m in Minkowski spacetime. The field involved is a real vector field A...
. The fields are
 and the action is
and the action is
where
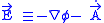
and
 .
.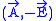 and
and 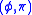 are canonical variables. The second class constraints are
are canonical variables. The second class constraints are
and
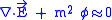 .
.The Hamiltonian is given by
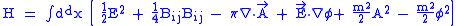 .
.1, N. K. Falck and A. C. Hirshfeld, 1983, "Dirac-bracket quantisation of a constrained nonlinear system: the rigid rotator", Eur. J. Phys. 4 p.5. doi: 10.1088/0143-0807/4/1/003 (Tote that the form of the quantum momentum in this paper is dubious.)
2, T. Homma, T. Inamoto, and T. Miyazaki, 1990, "Schrödinger equation for the nonrelativistic particle constrained on a hypersurface in a curved space ", Phys. Rev. D 42, p.2049. http://prd.aps.org/abstract/PRD/v42/i6/p2049_1. (Tote that the Hamiltonian suggested by the authors from second form of the constraint, (i.e., the time derivative of the
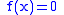 ) , is not completely compatible with the formalism of Hamiltonian mechanics.)
) , is not completely compatible with the formalism of Hamiltonian mechanics.)

