
Secret Sharing using the Chinese Remainder Theorem
Encyclopedia
Secret sharing
consists of recovering a secret S from a set of shares, each containing partial information about the secret. The Chinese remainder theorem
(CRT) states that for a given system of simultaneous congruence equations, the solution is unique in some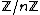 , with
, with 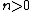 under some appropriate conditions on the congruences.
under some appropriate conditions on the congruences.
Secret sharing
can thus use the CRT to produce the shares presented in the congruence equations and the secret could be recovered by solving the system of congruences to get the unique solution, which will be the secret to recover.
schemes. The most basic types are the so-called threshold
schemes, where only the cardinality of the set of shares matters. In other words, given a secret S, and n shares, any set of t shares is a set with the smallest cardinality from which the secret can be recovered, in the sense that any set of t-1 shares is not enough to give S. This is known as a threshold access structure
. We call such schemes (t,n) threshold
secret sharing
schemes, or t-out-of-n scheme.
Threshold
secret sharing
schemes differ from one another by the method of generating the shares, starting from a certain secret. The first ones are Shamir's threshold secret sharing scheme
, which is based on polynomial interpolation
in order to find S from a given set of shares, and George Blakley
's geometric secret sharing scheme, which uses geometric methods to recover the secret S. Threshold
secret sharing
schemes based on the CRT are due to Mignotte and Asmuth-Bloom, they use special sequences of integers along with the CRT.
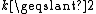 ,
, 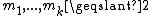 , and
, and 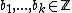 . The system of equations
. The system of equations
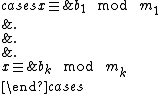
has solutions in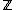 if and only if
if and only if 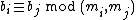 for all
for all 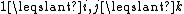 , where
, where 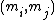 denotes the greatest common divisor
denotes the greatest common divisor
(GCD) of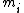 and
and 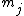 . Furthermore, under these conditions, the system has a unique solution in
. Furthermore, under these conditions, the system has a unique solution in 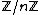 where
where 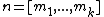 , which denotes the least common multiple
, which denotes the least common multiple
(LCM) of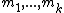 .
.
provides us with a method to uniquely determine a number S modulo k many relatively prime integers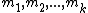 , given that
, given that 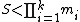 , then, the idea is to construct a scheme that will determine the secret S given any k shares (in this case, the remainder of S modulo each of the numbers
, then, the idea is to construct a scheme that will determine the secret S given any k shares (in this case, the remainder of S modulo each of the numbers 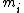 ), but will not reveal the secret given less than k of such shares.
), but will not reveal the secret given less than k of such shares.
Ultimately, we choose n relatively prime integers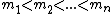 such that S is smaller than the product of any choice of k of these integers, but at the same time is greater than any choice of k-1 of them. Then the shares
such that S is smaller than the product of any choice of k of these integers, but at the same time is greater than any choice of k-1 of them. Then the shares 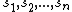 are defined by
are defined by 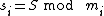 for
for 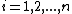 . In this manner, thanks to the CRT, we can uniquely determine S from any set of k or more shares, but not from less than k. This provides the so-called threshold access structure
. In this manner, thanks to the CRT, we can uniquely determine S from any set of k or more shares, but not from less than k. This provides the so-called threshold access structure
.
This condition on S can also be regarded as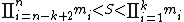 . Since S is smaller than the smallest product of k of the integers, it will be smaller than the product of any k of them. Also, being greater than the product of the greatest k-1 integers, it will be greater than the product of any k-1 of them.
. Since S is smaller than the smallest product of k of the integers, it will be smaller than the product of any k of them. Also, being greater than the product of the greatest k-1 integers, it will be greater than the product of any k-1 of them.
There are two Secret Sharing Schemes
that utilize essentially this idea, Mignotte's and Asmuth-Bloom's Schemes, which are explained below.
secret sharing
scheme uses, along with the CRT, special sequences of integers called the (k,n)-Mignotte sequences which consist of n integers, pairwise coprime
, such that the product of the smallest k of them is greater than the product of the k-1 biggest ones. This condition is crucial because the scheme is built on choosing the secret as an integer between the two products, and this condition ensures that at least k shares are needed to fully recover the secret, no matter how they are chosen.
Formally, let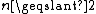 be an integer, and k be an integer such that
be an integer, and k be an integer such that 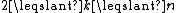 . A (k,n)-Mignotte sequence is a strictly increasing sequence of positive integers
. A (k,n)-Mignotte sequence is a strictly increasing sequence of positive integers 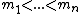 , with
, with 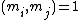 for all
for all 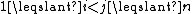 , such that
, such that 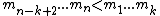 . We call this range the authorized range. Now, the scheme works as follows: We build a (k,n)-threshold
. We call this range the authorized range. Now, the scheme works as follows: We build a (k,n)-threshold
secret sharing
scheme. We choose the secret S as a random integer in the authorized range. We compute, for every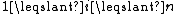 , the reduction modulo
, the reduction modulo 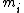 of S that we call
of S that we call 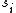 , these are the shares. Now, for any k different shares
, these are the shares. Now, for any k different shares 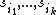 , we consider the system of congruences:
, we consider the system of congruences:
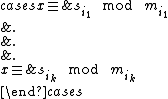
By the Chinese remainder theorem
, since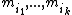 are pairwise coprime
are pairwise coprime
, the system has a unique solution modulo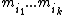 . By the construction of our shares, this solution is nothing but the secret S to recover.
. By the construction of our shares, this solution is nothing but the secret S to recover.
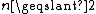 be an integer, and k be an integer such that
be an integer, and k be an integer such that 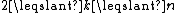 . We consider a sequence of pairwise coprime
. We consider a sequence of pairwise coprime
positive integers such that
such that 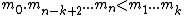 . For this given sequence, we choose the secret S as a random integer in the set
. For this given sequence, we choose the secret S as a random integer in the set 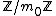 .
.
We then pick a random integer such that
such that 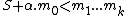 . We compute the reduction modulo
. We compute the reduction modulo 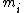 of
of 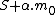 , for all
, for all 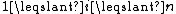 , these are the shares
, these are the shares 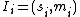 . Now, for any k different shares
. Now, for any k different shares 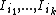 , we consider the system of congruences:
, we consider the system of congruences:
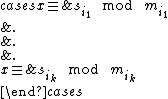
By the Chinese remainder theorem
, since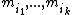 are pairwise coprime
are pairwise coprime
, the system has a unique solution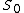 modulo
modulo 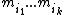 . By the construction of our shares, the secret S is the reduction modulo
. By the construction of our shares, the secret S is the reduction modulo 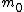 of
of 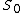
It is important to notice that the Mignotte and Asmuth-Bloom (k,n)-threshold
secret-sharing
schemes are not perfect schemes, in the sense that a set of less than k shares contains some information about the secret. Nevertheless, by a suitable choice of the sequences and the parameters ( in the Asmuth-Bloom case), one can get a reasonable security factor. This is why the Asmuth-Bloom scheme is more secure, for it involves more random parameters.
in the Asmuth-Bloom case), one can get a reasonable security factor. This is why the Asmuth-Bloom scheme is more secure, for it involves more random parameters.
integers being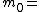 3,
3, 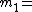 11,
11, 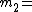 13,
13, 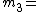 17 and
17 and 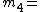 19. They satisfy the Asmuth-Bloom required sequence because
19. They satisfy the Asmuth-Bloom required sequence because 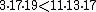 .
.
Say our secret S is 2. Pick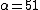 , satisfying the required condition for the Asmuth-Bloom scheme. Then
, satisfying the required condition for the Asmuth-Bloom scheme. Then 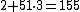 and we compute the shares for each of the integers 11, 13, 17 and 19. They are respectively 1, 12, 2 and 3. We consider one possible set of 3 shares: among the 4 possible sets of 3 shares we take the set {1,12,2} and show that it recovers the secret S=2. Consider the following system of congruences:
and we compute the shares for each of the integers 11, 13, 17 and 19. They are respectively 1, 12, 2 and 3. We consider one possible set of 3 shares: among the 4 possible sets of 3 shares we take the set {1,12,2} and show that it recovers the secret S=2. Consider the following system of congruences:
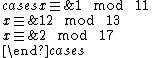
To solve the system, let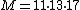 . From a constructive algorithm for solving such a system, we know that a solution to the system is
. From a constructive algorithm for solving such a system, we know that a solution to the system is 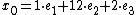 , where each
, where each 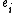 is found as follows:
is found as follows:
By Bézout's identity
, since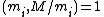 , there exist positive integers
, there exist positive integers 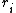 and
and 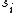 , that can be found using the Extended Euclidean algorithm
, that can be found using the Extended Euclidean algorithm
, such that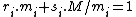 . Set
. Set 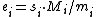 .
.
From the identities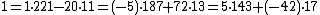 , we get that
, we get that 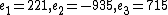 , and the unique solution modulo
, and the unique solution modulo 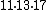 is 155. Finally,
is 155. Finally, 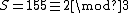 .
.
Secret sharing
Secret sharing refers to method for distributing a secret amongst a group of participants, each of whom is allocated a share of the secret. The secret can be reconstructed only when a sufficient number of shares are combined together; individual shares are of no use on their own.More formally, in a...
consists of recovering a secret S from a set of shares, each containing partial information about the secret. The Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
(CRT) states that for a given system of simultaneous congruence equations, the solution is unique in some
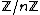 , with
, with 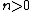 under some appropriate conditions on the congruences.
under some appropriate conditions on the congruences.Secret sharing
Secret sharing
Secret sharing refers to method for distributing a secret amongst a group of participants, each of whom is allocated a share of the secret. The secret can be reconstructed only when a sufficient number of shares are combined together; individual shares are of no use on their own.More formally, in a...
can thus use the CRT to produce the shares presented in the congruence equations and the secret could be recovered by solving the system of congruences to get the unique solution, which will be the secret to recover.
Secret sharing schemes: several types
There are several types of secret sharingSecret sharing
Secret sharing refers to method for distributing a secret amongst a group of participants, each of whom is allocated a share of the secret. The secret can be reconstructed only when a sufficient number of shares are combined together; individual shares are of no use on their own.More formally, in a...
schemes. The most basic types are the so-called threshold
Threshold cryptosystem
In cryptography, a cryptosystem is called a 'threshold cryptosystem', if in order to decrypt an encrypted message a number of parties exceeding a threshold is required to cooperate in the decryption protocol. The message is encrypted using a public key and the corresponding private key is shared...
schemes, where only the cardinality of the set of shares matters. In other words, given a secret S, and n shares, any set of t shares is a set with the smallest cardinality from which the secret can be recovered, in the sense that any set of t-1 shares is not enough to give S. This is known as a threshold access structure
Access structure
Access structures are used in the study of security system where multiple parties need to work together to obtain a resource. Groups of parties that are granted access are called qualified. In set theoretic terms they are referred to as qualified sets. In turn, the set of all such qualified sets is...
. We call such schemes (t,n) threshold
Threshold cryptosystem
In cryptography, a cryptosystem is called a 'threshold cryptosystem', if in order to decrypt an encrypted message a number of parties exceeding a threshold is required to cooperate in the decryption protocol. The message is encrypted using a public key and the corresponding private key is shared...
secret sharing
Secret sharing
Secret sharing refers to method for distributing a secret amongst a group of participants, each of whom is allocated a share of the secret. The secret can be reconstructed only when a sufficient number of shares are combined together; individual shares are of no use on their own.More formally, in a...
schemes, or t-out-of-n scheme.
Threshold
Threshold cryptosystem
In cryptography, a cryptosystem is called a 'threshold cryptosystem', if in order to decrypt an encrypted message a number of parties exceeding a threshold is required to cooperate in the decryption protocol. The message is encrypted using a public key and the corresponding private key is shared...
secret sharing
Secret sharing
Secret sharing refers to method for distributing a secret amongst a group of participants, each of whom is allocated a share of the secret. The secret can be reconstructed only when a sufficient number of shares are combined together; individual shares are of no use on their own.More formally, in a...
schemes differ from one another by the method of generating the shares, starting from a certain secret. The first ones are Shamir's threshold secret sharing scheme
Shamir's Secret Sharing
Shamir's Secret Sharing is an algorithm in cryptography. It is a form of secret sharing, where a secret is divided into parts, giving each participant its own unique part, where some of the parts or all of them are needed in order to reconstruct the secret....
, which is based on polynomial interpolation
Polynomial interpolation
In numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
in order to find S from a given set of shares, and George Blakley
George Blakley
George Robert Blakley Jr. is an American cryptographer and a professor of mathematics at Texas A&M University, best known for inventing a secret sharing scheme in 1979.-Biography:...
's geometric secret sharing scheme, which uses geometric methods to recover the secret S. Threshold
Threshold cryptosystem
In cryptography, a cryptosystem is called a 'threshold cryptosystem', if in order to decrypt an encrypted message a number of parties exceeding a threshold is required to cooperate in the decryption protocol. The message is encrypted using a public key and the corresponding private key is shared...
secret sharing
Secret sharing
Secret sharing refers to method for distributing a secret amongst a group of participants, each of whom is allocated a share of the secret. The secret can be reconstructed only when a sufficient number of shares are combined together; individual shares are of no use on their own.More formally, in a...
schemes based on the CRT are due to Mignotte and Asmuth-Bloom, they use special sequences of integers along with the CRT.
Chinese remainder theorem
Let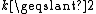 ,
, 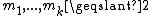 , and
, and 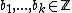 . The system of equations
. The system of equations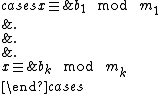
has solutions in
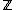 if and only if
if and only if 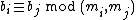 for all
for all 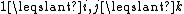 , where
, where 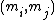 denotes the greatest common divisor
denotes the greatest common divisorGreatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
(GCD) of
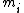 and
and 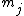 . Furthermore, under these conditions, the system has a unique solution in
. Furthermore, under these conditions, the system has a unique solution in 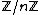 where
where 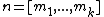 , which denotes the least common multiple
, which denotes the least common multipleLeast common multiple
In arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b...
(LCM) of
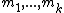 .
.Secret sharing using the CRT
Since the Chinese remainder theoremChinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
provides us with a method to uniquely determine a number S modulo k many relatively prime integers
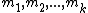 , given that
, given that 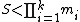 , then, the idea is to construct a scheme that will determine the secret S given any k shares (in this case, the remainder of S modulo each of the numbers
, then, the idea is to construct a scheme that will determine the secret S given any k shares (in this case, the remainder of S modulo each of the numbers 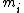 ), but will not reveal the secret given less than k of such shares.
), but will not reveal the secret given less than k of such shares.Ultimately, we choose n relatively prime integers
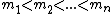 such that S is smaller than the product of any choice of k of these integers, but at the same time is greater than any choice of k-1 of them. Then the shares
such that S is smaller than the product of any choice of k of these integers, but at the same time is greater than any choice of k-1 of them. Then the shares 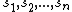 are defined by
are defined by 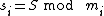 for
for 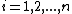 . In this manner, thanks to the CRT, we can uniquely determine S from any set of k or more shares, but not from less than k. This provides the so-called threshold access structure
. In this manner, thanks to the CRT, we can uniquely determine S from any set of k or more shares, but not from less than k. This provides the so-called threshold access structureAccess structure
Access structures are used in the study of security system where multiple parties need to work together to obtain a resource. Groups of parties that are granted access are called qualified. In set theoretic terms they are referred to as qualified sets. In turn, the set of all such qualified sets is...
.
This condition on S can also be regarded as
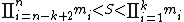 . Since S is smaller than the smallest product of k of the integers, it will be smaller than the product of any k of them. Also, being greater than the product of the greatest k-1 integers, it will be greater than the product of any k-1 of them.
. Since S is smaller than the smallest product of k of the integers, it will be smaller than the product of any k of them. Also, being greater than the product of the greatest k-1 integers, it will be greater than the product of any k-1 of them.There are two Secret Sharing Schemes
Secret sharing
Secret sharing refers to method for distributing a secret amongst a group of participants, each of whom is allocated a share of the secret. The secret can be reconstructed only when a sufficient number of shares are combined together; individual shares are of no use on their own.More formally, in a...
that utilize essentially this idea, Mignotte's and Asmuth-Bloom's Schemes, which are explained below.
Mignotte's threshold secret sharing scheme
As said before, Mignotte's thresholdThreshold cryptosystem
In cryptography, a cryptosystem is called a 'threshold cryptosystem', if in order to decrypt an encrypted message a number of parties exceeding a threshold is required to cooperate in the decryption protocol. The message is encrypted using a public key and the corresponding private key is shared...
secret sharing
Secret sharing
Secret sharing refers to method for distributing a secret amongst a group of participants, each of whom is allocated a share of the secret. The secret can be reconstructed only when a sufficient number of shares are combined together; individual shares are of no use on their own.More formally, in a...
scheme uses, along with the CRT, special sequences of integers called the (k,n)-Mignotte sequences which consist of n integers, pairwise coprime
Pairwise coprime
In mathematics, especially number theory, a set of integers is said to be pairwise coprime if every pair of distinct integers a and b in the set are coprime...
, such that the product of the smallest k of them is greater than the product of the k-1 biggest ones. This condition is crucial because the scheme is built on choosing the secret as an integer between the two products, and this condition ensures that at least k shares are needed to fully recover the secret, no matter how they are chosen.
Formally, let
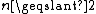 be an integer, and k be an integer such that
be an integer, and k be an integer such that 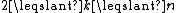 . A (k,n)-Mignotte sequence is a strictly increasing sequence of positive integers
. A (k,n)-Mignotte sequence is a strictly increasing sequence of positive integers 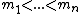 , with
, with 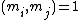 for all
for all 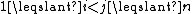 , such that
, such that 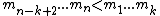 . We call this range the authorized range. Now, the scheme works as follows: We build a (k,n)-threshold
. We call this range the authorized range. Now, the scheme works as follows: We build a (k,n)-thresholdThreshold cryptosystem
In cryptography, a cryptosystem is called a 'threshold cryptosystem', if in order to decrypt an encrypted message a number of parties exceeding a threshold is required to cooperate in the decryption protocol. The message is encrypted using a public key and the corresponding private key is shared...
secret sharing
Secret sharing
Secret sharing refers to method for distributing a secret amongst a group of participants, each of whom is allocated a share of the secret. The secret can be reconstructed only when a sufficient number of shares are combined together; individual shares are of no use on their own.More formally, in a...
scheme. We choose the secret S as a random integer in the authorized range. We compute, for every
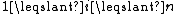 , the reduction modulo
, the reduction modulo 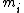 of S that we call
of S that we call 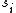 , these are the shares. Now, for any k different shares
, these are the shares. Now, for any k different shares 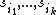 , we consider the system of congruences:
, we consider the system of congruences: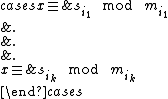
By the Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
, since
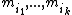 are pairwise coprime
are pairwise coprimePairwise coprime
In mathematics, especially number theory, a set of integers is said to be pairwise coprime if every pair of distinct integers a and b in the set are coprime...
, the system has a unique solution modulo
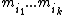 . By the construction of our shares, this solution is nothing but the secret S to recover.
. By the construction of our shares, this solution is nothing but the secret S to recover.Asmuth-Bloom's threshold secret sharing scheme
This scheme also uses special sequences of integers. Let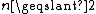 be an integer, and k be an integer such that
be an integer, and k be an integer such that 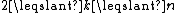 . We consider a sequence of pairwise coprime
. We consider a sequence of pairwise coprimePairwise coprime
In mathematics, especially number theory, a set of integers is said to be pairwise coprime if every pair of distinct integers a and b in the set are coprime...
positive integers
 such that
such that 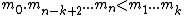 . For this given sequence, we choose the secret S as a random integer in the set
. For this given sequence, we choose the secret S as a random integer in the set 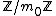 .
.We then pick a random integer
 such that
such that 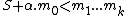 . We compute the reduction modulo
. We compute the reduction modulo 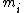 of
of 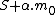 , for all
, for all 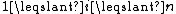 , these are the shares
, these are the shares 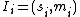 . Now, for any k different shares
. Now, for any k different shares 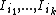 , we consider the system of congruences:
, we consider the system of congruences: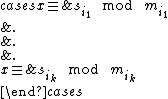
By the Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
, since
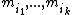 are pairwise coprime
are pairwise coprimePairwise coprime
In mathematics, especially number theory, a set of integers is said to be pairwise coprime if every pair of distinct integers a and b in the set are coprime...
, the system has a unique solution
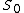 modulo
modulo 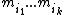 . By the construction of our shares, the secret S is the reduction modulo
. By the construction of our shares, the secret S is the reduction modulo 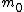 of
of 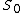
It is important to notice that the Mignotte and Asmuth-Bloom (k,n)-threshold
Threshold cryptosystem
In cryptography, a cryptosystem is called a 'threshold cryptosystem', if in order to decrypt an encrypted message a number of parties exceeding a threshold is required to cooperate in the decryption protocol. The message is encrypted using a public key and the corresponding private key is shared...
secret-sharing
Secret sharing
Secret sharing refers to method for distributing a secret amongst a group of participants, each of whom is allocated a share of the secret. The secret can be reconstructed only when a sufficient number of shares are combined together; individual shares are of no use on their own.More formally, in a...
schemes are not perfect schemes, in the sense that a set of less than k shares contains some information about the secret. Nevertheless, by a suitable choice of the sequences and the parameters (
 in the Asmuth-Bloom case), one can get a reasonable security factor. This is why the Asmuth-Bloom scheme is more secure, for it involves more random parameters.
in the Asmuth-Bloom case), one can get a reasonable security factor. This is why the Asmuth-Bloom scheme is more secure, for it involves more random parameters.Example
The following is an example on the Asmuth-Bloom's Scheme. For practical purposes we choose small values for all parameters. We choose k=3 and n=4. Our pairwise coprimePairwise coprime
In mathematics, especially number theory, a set of integers is said to be pairwise coprime if every pair of distinct integers a and b in the set are coprime...
integers being
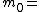 3,
3, 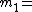 11,
11, 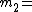 13,
13, 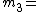 17 and
17 and 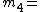 19. They satisfy the Asmuth-Bloom required sequence because
19. They satisfy the Asmuth-Bloom required sequence because 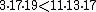 .
.Say our secret S is 2. Pick
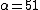 , satisfying the required condition for the Asmuth-Bloom scheme. Then
, satisfying the required condition for the Asmuth-Bloom scheme. Then 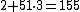 and we compute the shares for each of the integers 11, 13, 17 and 19. They are respectively 1, 12, 2 and 3. We consider one possible set of 3 shares: among the 4 possible sets of 3 shares we take the set {1,12,2} and show that it recovers the secret S=2. Consider the following system of congruences:
and we compute the shares for each of the integers 11, 13, 17 and 19. They are respectively 1, 12, 2 and 3. We consider one possible set of 3 shares: among the 4 possible sets of 3 shares we take the set {1,12,2} and show that it recovers the secret S=2. Consider the following system of congruences: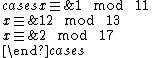
To solve the system, let
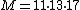 . From a constructive algorithm for solving such a system, we know that a solution to the system is
. From a constructive algorithm for solving such a system, we know that a solution to the system is 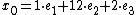 , where each
, where each 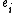 is found as follows:
is found as follows:By Bézout's identity
Bézout's identity
In number theory, Bézout's identity for two integers a, b is an expressionwhere x and y are integers , such that d is a common divisor of a and b. Bézout's lemma states that such coefficients exist for every pair of nonzero integers...
, since
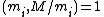 , there exist positive integers
, there exist positive integers 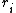 and
and 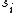 , that can be found using the Extended Euclidean algorithm
, that can be found using the Extended Euclidean algorithmExtended Euclidean algorithm
The extended Euclidean algorithm is an extension to the Euclidean algorithm. Besides finding the greatest common divisor of integers a and b, as the Euclidean algorithm does, it also finds integers x and y that satisfy Bézout's identityThe extended Euclidean algorithm is particularly useful when a...
, such that
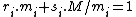 . Set
. Set 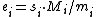 .
.From the identities
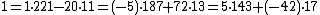 , we get that
, we get that 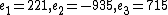 , and the unique solution modulo
, and the unique solution modulo 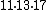 is 155. Finally,
is 155. Finally, 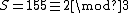 .
.See also
- Secret SharingSecret sharingSecret sharing refers to method for distributing a secret amongst a group of participants, each of whom is allocated a share of the secret. The secret can be reconstructed only when a sufficient number of shares are combined together; individual shares are of no use on their own.More formally, in a...
- Shamir's Secret Sharing SchemeShamir's Secret SharingShamir's Secret Sharing is an algorithm in cryptography. It is a form of secret sharing, where a secret is divided into parts, giving each participant its own unique part, where some of the parts or all of them are needed in order to reconstruct the secret....
- Chinese remainder theoremChinese remainder theoremThe Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
- Access StructureAccess structureAccess structures are used in the study of security system where multiple parties need to work together to obtain a resource. Groups of parties that are granted access are called qualified. In set theoretic terms they are referred to as qualified sets. In turn, the set of all such qualified sets is...

