
Section modulus
Encyclopedia
Section modulus is a geometric property for a given cross-section often used in the design of beams or flexural members. There are two types of section moduli, the elastic section modulus (S) and the plastic section modulus (Z).
3 (EN 1993 - Steel Design) resolves this by using W for both, but distinguishes between them by the use of subscripts - Wel and Wpl.
The elastic section modulus is determined by I / y, where I is the second moment of area
(or moment of inertia) and y is the distance from the neutral axis to any given fibre.. It is often reported using y = c, where c is the distance from the neutral axis to the most extreme compression fibre, as seen in the table below. It is also often used to determine the yield moment (My) such that My = S × σy, where σy is the yield strength
of the material.
The plastic section modulus depends on the location of the plastic neutral axis, or PNA. The PNA is defined as the axis that splits the cross section into two equal areas so that the area of compression equals the area of tension. So, for a square cross section the plastic and elastic neutral axis coincide, but given a T-shape for example, this isn't necessarily the case.
The plastic section modulus is then the sum of the areas of the cross section on each side of the PNA (which are equal) multiplied by the distance from the local centroids of the two areas to the PNA:
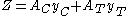
The plastic section modulus is used to calculate the plastic moment, Mp, or full capacity of a cross-section. The two terms are related by the yield strength of the material in question, Fy, by Mp=Fy*Z. Sometimes Z and S are related by defining a 'k' factor which is something of an indication of capacity beyond first yield. k=Z/S
Therefore for a rectangular section, k=1.5
Notation
North American and British/Australian convention reverse the usage of S & Z. Elastic modulus is S in North America, but Z in Britain/Australia, and vice versa for the plastic modulus. EurocodeEurocode
Eurocodes are a set of harmonized technical rules developed by the European Committee for Standardisation for the structural design of construction works in the European Union.The purposes of the Eurocodes are:...
3 (EN 1993 - Steel Design) resolves this by using W for both, but distinguishes between them by the use of subscripts - Wel and Wpl.
Elastic section modulus
For general design, the elastic section modulus is used, applying up to the yield point for most metals and other common materials.The elastic section modulus is determined by I / y, where I is the second moment of area
Second moment of area
The second moment of area, also known as the area moment of inertia, moment of inertia of plane area, or second moment of inertia is a property of a cross section that can be used to predict the resistance of beams to bending and deflection, around an axis that lies in the cross-sectional plane...
(or moment of inertia) and y is the distance from the neutral axis to any given fibre.. It is often reported using y = c, where c is the distance from the neutral axis to the most extreme compression fibre, as seen in the table below. It is also often used to determine the yield moment (My) such that My = S × σy, where σy is the yield strength
Yield (engineering)
The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
of the material.
| Cross-sectional shape | Figure | Equation | Comment |
|---|---|---|---|
| Rectangle | 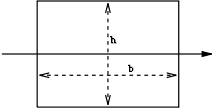 |
 |
Solid arrow represents neutral axis Neutral axis The neutral axis is an axis in the cross section of a beam or shaft along which there are no longitudinal stresses or strains. If the section is symmetric, isotropic and is not curved before a bend occurs, then the neutral axis is at the geometric centroid... |
| doubly symmetric -section I-beam -beams, also known as H-beams, W-beams , rolled steel joist , or double-T are beams with an - or H-shaped cross-section. The horizontal elements of the "" are flanges, while the vertical element is the web... (strong axis) |
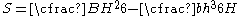 |
NA indicates neutral axis Neutral axis The neutral axis is an axis in the cross section of a beam or shaft along which there are no longitudinal stresses or strains. If the section is symmetric, isotropic and is not curved before a bend occurs, then the neutral axis is at the geometric centroid... |
|
| doubly symmetric -section I-beam -beams, also known as H-beams, W-beams , rolled steel joist , or double-T are beams with an - or H-shaped cross-section. The horizontal elements of the "" are flanges, while the vertical element is the web... (weak axis) |
 |
NA indicates neutral axis Neutral axis The neutral axis is an axis in the cross section of a beam or shaft along which there are no longitudinal stresses or strains. If the section is symmetric, isotropic and is not curved before a bend occurs, then the neutral axis is at the geometric centroid... |
|
| Circle |  |
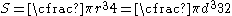 |
Solid arrow represents neutral axis Neutral axis The neutral axis is an axis in the cross section of a beam or shaft along which there are no longitudinal stresses or strains. If the section is symmetric, isotropic and is not curved before a bend occurs, then the neutral axis is at the geometric centroid... |
| Circular tube | 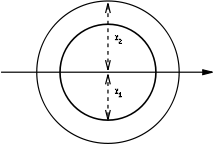 |
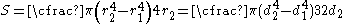 |
Solid arrow represents neutral axis Neutral axis The neutral axis is an axis in the cross section of a beam or shaft along which there are no longitudinal stresses or strains. If the section is symmetric, isotropic and is not curved before a bend occurs, then the neutral axis is at the geometric centroid... |
| Rectangular tube | 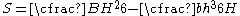 |
NA indicates neutral axis Neutral axis The neutral axis is an axis in the cross section of a beam or shaft along which there are no longitudinal stresses or strains. If the section is symmetric, isotropic and is not curved before a bend occurs, then the neutral axis is at the geometric centroid... |
|
| Diamond |  |
NA indicates neutral axis Neutral axis The neutral axis is an axis in the cross section of a beam or shaft along which there are no longitudinal stresses or strains. If the section is symmetric, isotropic and is not curved before a bend occurs, then the neutral axis is at the geometric centroid... |
|
| C-channel |  |
NA indicates neutral axis Neutral axis The neutral axis is an axis in the cross section of a beam or shaft along which there are no longitudinal stresses or strains. If the section is symmetric, isotropic and is not curved before a bend occurs, then the neutral axis is at the geometric centroid... |
|
Plastic section modulus
The Plastic section modulus is used for materials where (irreversible) plastic behaviour is dominant. The majority of designs do not intentionally encounter this behaviour.The plastic section modulus depends on the location of the plastic neutral axis, or PNA. The PNA is defined as the axis that splits the cross section into two equal areas so that the area of compression equals the area of tension. So, for a square cross section the plastic and elastic neutral axis coincide, but given a T-shape for example, this isn't necessarily the case.
The plastic section modulus is then the sum of the areas of the cross section on each side of the PNA (which are equal) multiplied by the distance from the local centroids of the two areas to the PNA:
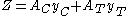
| Rectangular section |  |
|
| For the two flanges of an -beam I-beam -beams, also known as H-beams, W-beams , rolled steel joist , or double-T are beams with an - or H-shaped cross-section. The horizontal elements of the "" are flanges, while the vertical element is the web... with the web excluded |
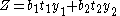 |
where: 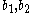 =width, =width, 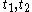 =thickness, =thickness,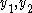 are the distances from the neutral axis to the centroids of the flanges respectively. are the distances from the neutral axis to the centroids of the flanges respectively. |
| Solid Circle | 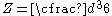 |
|
| Hollow Circle | 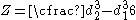 |
|
The plastic section modulus is used to calculate the plastic moment, Mp, or full capacity of a cross-section. The two terms are related by the yield strength of the material in question, Fy, by Mp=Fy*Z. Sometimes Z and S are related by defining a 'k' factor which is something of an indication of capacity beyond first yield. k=Z/S
Therefore for a rectangular section, k=1.5
External links
- http://www.engineeringtoolbox.com/american-wide-flange-steel-beams-d_1318.html - List of section moduli for common beam shapes
- http://www.novanumeric.com/samples.php?CalcName=SectionModulus - Online Calculation for Section Modulus

