The neutral axis is an axis in the cross section of a beam

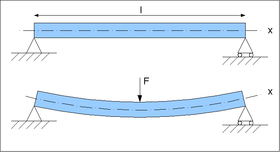
Beam (structure)

A beam is a horizontal structural element that is capable of withstanding load primarily by resisting bending. The bending force induced into the material of the beam as a result of the external loads, own weight, span and external reactions to these loads is called a bending moment.- Overview...

 or shaft along which there are no longitudinal stresses or strains. If the section is symmetric, isotropic and is not curved before a bend occurs, then the neutral axis is at the geometric centroid

Centroid

In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...

. All fibers on one side of the neutral axis are in a state of tension, while those on the opposite side are in compression

Since the beam is undergoing uniform bending, a plane on the beam remains plane. That is:



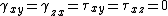
Where 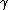is the shear strain and is the shear stress

Shear stress

A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...

There is a compressive (negative) strain at the top of the beam, and a tensile (positive) strain at the bottom of the beam. Therefore by the Intermediate Value Theorem, there must be some point in between the top and the bottom that has no strain, since the strain in a beam is a continuous function

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

.

Let L be the original length of the beam (span

Span (architecture)

Span is the distance between two intermediate supports for a structure, e.g. a beam or a bridge.A span can be closed by a solid beam or of a rope...

)

ε(y) is the strain as a function of coordinate on the face of the beam.

σ(y) is the stress as a function of coordinate on the face of the beam.

ρ is the radius of curvature

Radius of curvature

The distance from the center of a circle or sphere to its surface is its radius. For other curved lines or surfaces, the radius of curvature at a given point is the radius of a circle that mathematically best fits the curve at that point....

 of the beam at its neutral axis.

θ is the bend

Bending

In engineering mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically...

 angle

Angle

In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...

Since the bending is uniform

Uniform

A uniform is a set of standard clothing worn by members of an organization while participating in that organization's activity. Modern uniforms are worn by armed forces and paramilitary organizations such as police, emergency services, security guards, in some workplaces and schools and by inmates...

 and pure, there is therefore at a distance y from the neutral axis with the inherent property of having no strain:



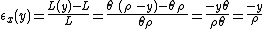
Therefore the longitudinal normal strain 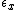varies linearly with the distance y from the neutral surface. Denoting 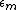as the maximum strain in the beam (at a distance c from the neutral axis), it becomes clear that: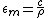



Therefore, we can solve for ρ, and find that:



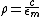
Substituting this back into the original expression, we find that:



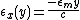
Due to Hooke's Law

Hooke's law

In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...

, the stress in the beam is proportional to the strain by E, the modulus of Elasticity:



Therefore:





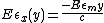
From statics

Statics

Statics is the branch of mechanics concerned with the analysis of loads on physical systems in static equilibrium, that is, in a state where the relative positions of subsystems do not vary over time, or where components and structures are at a constant velocity...

, a moment (i.e. pure bending

Pure bending

Pure bending is a condition of stress where a bending moment is applied to a beam without the simultaneous application of axial, shear, or torsional forces....

) consists of equal and opposite forces. Therefore, the total amount of stress across the cross section must be 0.



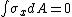
Therefore:



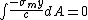
Since y denotes the distance from the neutral axis to any point on the face, it is the only variable that changes with respect to dA. Therefore:



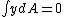
Therefore the first moment of the cross section about its neutral axis must be zero. Therefore the neutral axis lies on the centroid of the cross section.

Note that the neutral axis does not change in length when under bending. It may seem counterintuitive at first, but this is because there are no bending stresses in the neutral axis. However, there are shear stresses (τ) in the neutral axis, zero in the middle of the span but increasing towards the supports, as can be seen in this function (Jourawski's formula);


where

T = shear force

Q = first moment of area

First moment of area

The first moment of area, sometimes misnamed as the first moment of inertia, is based in the mathematical construct moments in metric spaces, stating that the moment of area equals the summation of area times distance to an axis [Σ]...

 of the section above/below the neutral axis

w = width of the beam

I = second moment of area

Second moment of area

The second moment of area, also known as the area moment of inertia, moment of inertia of plane area, or second moment of inertia is a property of a cross section that can be used to predict the resistance of beams to bending and deflection, around an axis that lies in the cross-sectional plane...

 of the beam

This definition is suitable for the so-called long beams, i.e. its length is much larger than the other two dimensions.

Arches

Arches also have a neutral axis. If they are made of stone; stone is an inelastic medium, and has little strength in tension. Therefore as the loading on the arch changes the neutral axis moves- if the neutral axis leaves the stonework, then the arch will fail.
This theory (also known as the thrust line method) was proposed by Thomas Young

Thomas Young (scientist)

Thomas Young was an English polymath. He is famous for having partly deciphered Egyptian hieroglyphics before Jean-François Champollion eventually expanded on his work...

 and developed by Isambard Kingdom Brunel

Isambard Kingdom Brunel

Isambard Kingdom Brunel, FRS , was a British civil engineer who built bridges and dockyards including the construction of the first major British railway, the Great Western Railway; a series of steamships, including the first propeller-driven transatlantic steamship; and numerous important bridges...

.

External links

• Proof that the centroid lies on neutral axis