Radius of curvature
Encyclopedia
The distance from the center of a circle or sphere
to its surface is its radius
. For other curved lines or surfaces, the radius of curvature at a given point is the radius of a circle that mathematically best fits the curve at that point.
The equivalent "surface radius" that is described by radial distances at points along a body's surface is its radius of curvature (more formally, the radius of curvature of a curve at a point is the radius of the osculating circle
at that point).
With a sphere, the radius of curvature equals the radius. With an oblate ellipsoid (or, more properly, an oblate spheroid), however, not only does it differ from the radius, but it varies, depending on the direction being faced. The extremes are known as the principal radii of curvature.
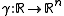is a parameterized curve in 
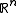then the radius of curvature at each point of the curve, 
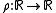, is given by
.
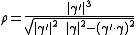As a special case, if f(t) is a function from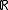
to 
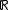, then the curvature of its graph
,
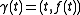, is
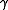be as above, and fix 
. We want to find the radius 
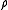of a parameterized circle which matches 
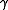in its zeroth, first, and second derivatives at 
. Clearly the radius will not depend on the position (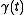
), only on the velocity (
) and acceleration (
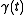). There are only three independent scalars that can be obtained from two vectors v and w, namely v·v, v·w, and w·w. Thus the radius of curvature must be a function of the three scalars 
, 
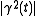and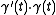 
.
The general equation for a parameterized circle in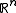
is
where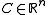
is the center of the circle (irrelevant since it disappears in the derivatives), 
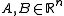are perpendicular vectors of length 
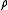(that is, 
and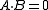 
), and 
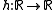is an arbitrary function which is twice differentiable at t.
The relevant derivatives of g work out to be
If we now equate these derivatives of g to the corresponding derivatives of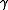
at t we obtain
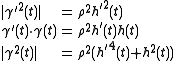
These three equations in three unknowns (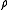
, 
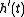and 
) can be solved for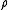 
, giving the formula for the radius of curvature:
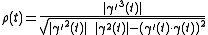
or, omitting the parameter (t) for readability,
.
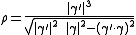, a, and the polar radius, or semi-minor axis
, b. The "ellipticalness" of any ellipsoid, like any ellipse, is measured in different ways (e.g., eccentricity
and flattening
), any and all of which are trigonometric functions of
its angular eccentricity
,
:
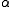The primary parameter utilized in identifying a point's vertical position is its latitude
.
A latitude can be expressed either directly or from the arcsine of a trigonometric product, the arguments (i.e., a function's "input") of the factors being the arc path (which defines, and is the azimuth at the equator of, a given great circle
, or its elliptical counterpart) and the transverse colatitude, which is a corresponding, vertical latitude ring that defines a point along an arc path/great circle. The relationship can be remembered by the terms' initial letter, L-A-T:
Therefore, along a north-south arc path (which equals 0°), the primary quadrant form of latitude equals the transverse colatitude's at a given point.
As most introductory discussions of curvature and their radius identify position in terms of latitude, this article will too, with only the added inclusion of a "0" placeholder for more advanced discussions where the arc path is actively utilized:
There are two types of latitude commonly employed in these discussions, the planetographic (or planetodetic; for Earth, the customized terms are "geographic" and "geodetic") and reduced latitudes,
and 
(respectively):
The calculation of elliptic quantities usually involves different elliptic integral
s, the most basic integrands being
and its complement, 
:
Thus
.
, then, is the state and degree of deviation from a straight line—i.e., an "arced line".
There are different interpretations of curvature, depending on such things as the planular angle the given arc is dividing and the direction being faced at the surface's point.
What is concerned with here is normal curvature, where "normal" refers to orthogonality
, or perpendicularity.
There are two principal curvature
s identified, a maximum, κ1, and a minimum, κ2.
The spot of least curvature on an oblate spheroid is at the poles, where the principal curvatures converge (as there is only one facing direction——towards the planetographic equator!) and the surface is most flattened.
Therefore, there are two principal radii of curvature: A vertical, corresponding to κ1, and a horizontal, corresponding to κ2. Most introductions to the principal radii of curvature provide explanations independent to their curvature counterparts, focusing more on positioning and angle, rather than shape and contortion.
Radius of curvature is also used in a three part equation for bending of beams
.
, the distance from the center of the spheroid to the equator; the second may be 
, the slightly-smaller distance from the spheroid center to the pole, or it may be the dimensionless number 
expressing the difference between the two spheroid dimensions
For the WGS84 spheroid, now commonly used,
is set to be 6378137 meters exactly and 
is set to be 298.257223563 exactly (which makes 
about 6356752.3142 meters).
Another dimensionless number is
, the eccentricity squared of the spheroid
(Irrelevant aside: if we look at a cross-sectional ellipse containing the spheroid's pole-to-pole axis, the eccentricity
is the distance from the center of the ellipse to a focus, divided by 
, the longer half-axis of the ellipse. In other words, if the eccentricity of an ellipse is 0.5, each focus is halfway from the center of the ellipse to its end.)
If we cross-section the spheroid with a vertical north-south plane, the radius of curvature of the resulting ellipse at latitude
is
The radius of curvature of the ellipse cross-sectioned by a vertical east-west plane through a point at latitude
is
(Irrelevant aside: N is also the distance from the point to the spheroid's axis, measured along the straight line that is vertical at the point.)
Another of Euler's many formulas
gives the radius of curvature of the ellipse cross-sectioned by a vertical plane in some direction other than north-south or east-west
where
is the azimuth of the line at the point: north equals zero, east equals 90 degrees. At the pole M = N, but at any other point M is the minimum radius of curvature of all the possible vertical cross-sections through that point, while N is the maximum.
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
to its surface is its radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
. For other curved lines or surfaces, the radius of curvature at a given point is the radius of a circle that mathematically best fits the curve at that point.
The equivalent "surface radius" that is described by radial distances at points along a body's surface is its radius of curvature (more formally, the radius of curvature of a curve at a point is the radius of the osculating circle
Osculating circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...
at that point).
With a sphere, the radius of curvature equals the radius. With an oblate ellipsoid (or, more properly, an oblate spheroid), however, not only does it differ from the radius, but it varies, depending on the direction being faced. The extremes are known as the principal radii of curvature.
Explanation
Imagine driving a car on a curvy road on a completely flat plain (so that the geographic plain is a geometric plane). At any one point along the way, lock the steering wheel in its position, so that the car thereafter follows a perfect circle. The car will, of course, deviate from the road, unless the road is also a perfect circle. The radius of that circle the car makes is the radius of curvature of the curvy road at the point at which the steering wheel was locked. The more sharply curved the road is at the point you locked the steering wheel, the smaller the radius of curvature.Formula
If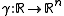 is a parameterized curve in 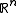then the radius of curvature at each point of the curve, 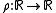, is given by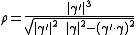.As a special case, if f(t) is a function from
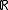to 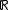, then the curvature of its graphGraph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane 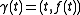is...
,
, isDerivation
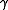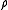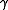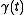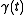Let be as above, and fix . We want to find the radius of a parameterized circle which matches in its zeroth, first, and second derivatives at . Clearly the radius will not depend on the position (), only on the velocity () and acceleration (). There are only three independent scalars that can be obtained from two vectors v and w, namely v·v, v·w, and w·w. Thus the radius of curvature must be a function of the three scalars , 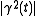and 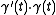.The general equation for a parameterized circle in
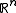is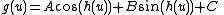where
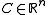is the center of the circle (irrelevant since it disappears in the derivatives), 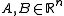are perpendicular vectors of length 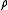(that is, and 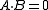), and 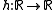is an arbitrary function which is twice differentiable at t.The relevant derivatives of g work out to be
If we now equate these derivatives of g to the corresponding derivatives of
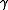at t we obtain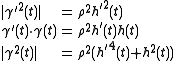These three equations in three unknowns (
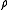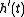, and ) can be solved for 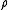, giving the formula for the radius of curvature: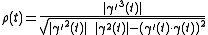or, omitting the parameter (t) for readability,
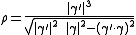.Elliptic, latitudinal components
The radius extremes of an oblate spheroid are the equatorial radius, or semi-major axisSemi-major axis
The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
, a, and the polar radius, or semi-minor axis
Semi-minor axis
In geometry, the semi-minor axis is a line segment associated with most conic sections . One end of the segment is the center of the conic section, and it is at right angles with the semi-major axis...
, b. The "ellipticalness" of any ellipsoid, like any ellipse, is measured in different ways (e.g., eccentricity
Eccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
and flattening
Flattening
The flattening, ellipticity, or oblateness of an oblate spheroid is a measure of the "squashing" of the spheroid's pole, towards its equator...
), any and all of which are trigonometric functions of
its angular eccentricity
Angular eccentricity
In the study of ellipses and related geometry, various parameters in the distortion of a circle into an ellipse are identified and employed: Aspect ratio, flattening and eccentricity....
,
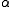:The primary parameter utilized in identifying a point's vertical position is its latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
.
A latitude can be expressed either directly or from the arcsine of a trigonometric product, the arguments (i.e., a function's "input") of the factors being the arc path (which defines, and is the azimuth at the equator of, a given great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
, or its elliptical counterpart) and the transverse colatitude, which is a corresponding, vertical latitude ring that defines a point along an arc path/great circle. The relationship can be remembered by the terms' initial letter, L-A-T:
Therefore, along a north-south arc path (which equals 0°), the primary quadrant form of latitude equals the transverse colatitude's at a given point.
As most introductory discussions of curvature and their radius identify position in terms of latitude, this article will too, with only the added inclusion of a "0" placeholder for more advanced discussions where the arc path is actively utilized:
There are two types of latitude commonly employed in these discussions, the planetographic (or planetodetic; for Earth, the customized terms are "geographic" and "geodetic") and reduced latitudes,
and (respectively):The calculation of elliptic quantities usually involves different elliptic integral
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
s, the most basic integrands being
and its complement, :Thus
.Curvature
A simple, if crude, definition of a circle is "a curved line bent in equal proportions, where its endpoints meet". CurvatureCurvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
, then, is the state and degree of deviation from a straight line—i.e., an "arced line".
There are different interpretations of curvature, depending on such things as the planular angle the given arc is dividing and the direction being faced at the surface's point.
What is concerned with here is normal curvature, where "normal" refers to orthogonality
Orthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
, or perpendicularity.
There are two principal curvature
Principal curvature
In differential geometry, the two principal curvatures at a given point of a surface are the eigenvalues of the shape operator at the point. They measure how the surface bends by different amounts in different directions at that point.-Discussion:...
s identified, a maximum, κ1, and a minimum, κ2.
Meridional maximum
- The arc in the meridional, north-south vertical direction at the planetographic equator possesses the maximum curvature, where it "pinches", thereby being the least straight.
Perpendicular minimum
- The perpendicular, horizontally directed arc contains the least curvature at the equator, as the equatorial circumference is——at least in mathematical definition——perfectly circular.
The spot of least curvature on an oblate spheroid is at the poles, where the principal curvatures converge (as there is only one facing direction——towards the planetographic equator!) and the surface is most flattened.
Merged curvature
- There are two universally recognized blendings of the principal curvatures: The arithmetic meanArithmetic meanIn mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
is known as the mean curvatureMean curvatureIn mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
, H, while the squared geometric meanGeometric meanThe geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
——or simply the product——is known as the Gaussian curvatureGaussian curvatureIn differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
, K:
Principal radii of curvature
A curvature's radius, RoC, is simply its reciprocal:Therefore, there are two principal radii of curvature: A vertical, corresponding to κ1, and a horizontal, corresponding to κ2. Most introductions to the principal radii of curvature provide explanations independent to their curvature counterparts, focusing more on positioning and angle, rather than shape and contortion.
Meridional radius of curvature
- The vertical radius of curvature is parallel to the "principal vertical", which is the facing, central meridian and is known as the meridional radius of curvature, M (alternatively, R1 or p):
-
- (Crossing the planetographic equator,
.)
- (Crossing the planetographic equator,
Normal radius of curvature
- The horizontal radius of curvature is perpendicular (again, meaning "normal" or "orthogonalOrthogonalityOrthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
") to the central meridian, but parallel to a great arc (be it spherical or elliptical) as it crosses the "prime vertical", or transverse equator (i.e., the meridian 90° away from the facing principal meridian——the "horizontal meridian"), and is known as the transverse (equatorial), or normal, radius of curvature, N (alternatively, R2 or v):
-
- (Along the planetographic equator, which is an ellipsoid's
- only true great circle,
.)
Polar convergence
- Just as with the curvature, at the poles M and N converge, resulting in an equal radius of curvature:
-
Merged radius of curvature
- There are two possible, basic "means":
-
-
- Mean radius of curvature, which is the arithmetic meanArithmetic meanIn mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
:
- Mean radius of curvature, which is the arithmetic mean
-
-
-
- Radius of mean curvature, which is the harmonic meanHarmonic meanIn mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired....
:
- Radius of mean curvature, which is the harmonic mean
-
- If these means are then arithmetically and harmonically averaged together, with the results reaveraged until the two averages converge, the result will be the arithmetic-harmonic mean, which equals the geometric mean and, in turn, equals the square root of the inverse of Gaussian curvature!
- While, at first glance, the squared form may be regarded as either the "radius of Gaussian curvature", "radius of Gaussian curvature2" or "radius2 of Gaussian Curvature", none of these terms quite fit, as Gaussian Curvature is the product of two curvatures, rather than a singular curvature.
Applications and examples
- For the use in differential geometry, see Cesàro equationCesàro equationIn geometry, the Cesàro equation of a plane curve is an equation relating curvature to arc length . It may also be given as an equation relating the radius of curvature to arc length. Two congruent curves will have the same Cesàro equation...
.
Radius of curvature is also used in a three part equation for bending of beams
Beam (structure)
A beam is a horizontal structural element that is capable of withstanding load primarily by resisting bending. The bending force induced into the material of the beam as a result of the external loads, own weight, span and external reactions to these loads is called a bending moment.- Overview...
.
Radius of curvature on the Earth
This section gives the formulas needed to calculate the radius of curvature of the spheroid used to approximate the surface of the Earth. The notation used in this section may or may not agree with that used in the rest of the article.Specifying the spheroid
Numerous spheroids have been used in the past to approximate the Earth's surface; each of them is defined by two numbers. Usually one is, the distance from the center of the spheroid to the equator; the second may be , the slightly-smaller distance from the spheroid center to the pole, or it may be the dimensionless number expressing the difference between the two spheroid dimensions-
(
is also known as 
, the reciprocal of the flattening)
For the WGS84 spheroid, now commonly used,
is set to be 6378137 meters exactly and is set to be 298.257223563 exactly (which makes about 6356752.3142 meters).Another dimensionless number is
, the eccentricity squared of the spheroid
(Irrelevant aside: if we look at a cross-sectional ellipse containing the spheroid's pole-to-pole axis, the eccentricity
is the distance from the center of the ellipse to a focus, divided by , the longer half-axis of the ellipse. In other words, if the eccentricity of an ellipse is 0.5, each focus is halfway from the center of the ellipse to its end.)Formulas
At any given point on the spheroid, a vertical plane is a plane containing the vertical line through that point; we're going to pretend that the vertical line is the line perpendicular to the surface of the spheroid at that point. (On the real earth that isn't quite right, but it's just a semantic error; the line that's perpendicular to the spheroid surface exists, and calling it "vertical" is easier than calling it something else that would be strictly correct.)If we cross-section the spheroid with a vertical north-south plane, the radius of curvature of the resulting ellipse at latitude
is
The radius of curvature of the ellipse cross-sectioned by a vertical east-west plane through a point at latitude
is
(Irrelevant aside: N is also the distance from the point to the spheroid's axis, measured along the straight line that is vertical at the point.)
Another of Euler's many formulas
Euler's theorem (differential geometry)
In the mathematical field of differential geometry, Euler's theorem is a result on the curvature of curves on a surface. The theorem establishes the existence of principal curvatures and associated principal directions which give the directions in which the surface curves the most and the least...
gives the radius of curvature of the ellipse cross-sectioned by a vertical plane in some direction other than north-south or east-west
where
is the azimuth of the line at the point: north equals zero, east equals 90 degrees. At the pole M = N, but at any other point M is the minimum radius of curvature of all the possible vertical cross-sections through that point, while N is the maximum.See also
- AFM probeAFM probeConsumable and measuring device with a sharp tip on the free swinging end of a cantilever which is protruding from a holder plate used in Atomic force microscopes . The dimensions of the cantilever are in the scale of micrometers. The radius of the tip is in the scale of a few nanometers...
- Base curve radiusBase curve radiusBase curve radius or simply base curve, abbreviated BCR or BC, is the measure of one important parameter of a lens in optometry. On a spectacle lens, it is the flatter curvature of the front surface and on a contact lens it is the curvature of the back surface. Typical values for a contact lens are...
- Bend radiusBend radiusBend radius, which is measured to the inside curvature, is the minimum radius one can bend a pipe, tube, sheet, cable or hose without kinking it, damaging it, or shortening its life. The smaller the bend radius, the greater is the material flexibility...
- CurveCurveIn mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
- CurvatureCurvatureIn mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
- Degree of curvatureDegree of curvatureDegree of curve or degree of curvature is a measure of curvature of a circular arc used in civil engineering for its easy use in layout surveying....
, civil engineering
- DiameterDiameterIn geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
- Minimum railway curve radiusMinimum railway curve radiusThe minimum railway curve radius, the shortest design radius, has an important bearing on constructions costs and operating costs and, in combination with superelevation in the case of train tracks, determines the maximum safe speed of a curve. Superelevation is not a factor on tramway tracks...
- Radius of curvature (optics)Radius of curvature (optics)Radius of curvature has specific meaning and sign convention in optical design. A spherical lens or mirror surface has a center of curvature located in either along or decentered from the system local optical axis. The vertex of the lens surface is located on the local optical axis...
- Reverse curveReverse curveIn civil engineering, a reverse curve is a section of the horizontal alignment of a highway or railroad route in which a curve to the left or right is followed immediately by a curve in the opposite direction....
- Track transition curveTrack transition curveA track transition curve, or spiral easement, is a mathematically calculated curve on a section of highway, or railroad track, where a straight section changes into a curve. It is designed to prevent sudden changes in centripetal force...
- Transition curve
External links
- USIGS Glossary (Definitions of "transverse" terms)
- The Geometry Center: Principal Curvatures
- 15.3 Curvature and Radius of Curvature