Sector (instrument)
Encyclopedia
Proportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
, trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
and division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
, and for various functions, such as squares
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
and cube roots. Its several scales permitted easy and direct solutions of problems in gunnery
Gun
A gun is a muzzle or breech-loaded projectile-firing weapon. There are various definitions depending on the nation and branch of service. A "gun" may be distinguished from other firearms in being a crew-served weapon such as a howitzer or mortar, as opposed to a small arm like a rifle or pistol,...
, surveying
Surveying
See Also: Public Land Survey SystemSurveying or land surveying is the technique, profession, and science of accurately determining the terrestrial or three-dimensional position of points and the distances and angles between them...
and navigation
Navigation
Navigation is the process of monitoring and controlling the movement of a craft or vehicle from one place to another. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks...
. The sector derives its name from the fourth proposition of the sixth book of Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
, where it is demonstrated that similar triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s have their like sides proportional. It has four parts, two legs with a pivot (the articulation), a quadrant and a clamp (the curved part at the end of the leg) that enables the compass to function as a gunner's quadrant.
History
The sector was invented, essentially simultaneously and independently, by a number of different people just prior to the start of the 17th century. The credit is usually given to either Thomas HoodThomas Hood (mathematician)
Thomas Hood was an English mathematician and physician, the first lecturer in mathematics appointed in England, a few years before the founding of Gresham College. He publicized the Copernican theory, and discussed the nova SN 1572....
, a British mathematician, or to the Italian mathematician and astronomer Galileo Galilei
Galileo Galilei
Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
. Galileo, with the help of his personal instrument maker Marc'Antonio Mazzoleni
Marc'Antonio Mazzoleni
Marc'Antonio Mazzoleni was a Paduan instrument maker best known for his association with Galileo Galilei, for whom Mazzoleni produced instruments including Galileo's military compasses and other instruments....
, created more than 100 copies of his military compass design and trained students in its use. Of the two credited inventors, Galileo is certainly the most famous, and earlier studies usually attributed its invention to him.
The Scales
The following is a description of the instrument as it was constructed by Galileo, and for which he wrote a popular manual. The terminating values are arbitrary and varied from manufacturer to manufacturer.The Arithmetic Lines
The innermost scales of the instrument are called the Arithmetic Lines from their division in arithmetical progression, that is, by equal additions which proceed out to the number 250. It is a linear scaleLinear scale
A linear scale, also called a bar scale, scale bar, graphic scale, or graphical scale, is a means of visually showing the scale of a map, nautical chart, engineering drawing, or architectural drawing....
generated by the function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
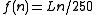, where n is an integer between 1 and 250, inclusive, and L is the length at mark 250.The Geometric Lines
The next scales are called the Geometric Lines and are divided in geometric progressionGeometric progression
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
out to 50. The lengths on the geometric lines vary as the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of the labeled values. If L represents the length at 50, then the generating function is:
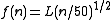, where n is a positive integer less than or equal to 50.The Stereometric Lines
The Stereometric Lines are so called because their divisions are according to the ratioRatio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
s of solid bodies, out to 148. One of this scale's applications is to calculate, when given one side of any solid body, the side of a similar one that has a given volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
ratio to the first. If L is the scale length at 148, then the scale-generating function is:
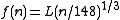, where n is a positive integer less than or equal to 148.The Metallic Lines
These lines have divisions on which appeared these symbols: Au, Pb, Ag, Cu, Fe, Sn, Mar, Sto, (GoldGold
Gold is a chemical element with the symbol Au and an atomic number of 79. Gold is a dense, soft, shiny, malleable and ductile metal. Pure gold has a bright yellow color and luster traditionally considered attractive, which it maintains without oxidizing in air or water. Chemically, gold is a...
, Lead
Lead
Lead is a main-group element in the carbon group with the symbol Pb and atomic number 82. Lead is a soft, malleable poor metal. It is also counted as one of the heavy metals. Metallic lead has a bluish-white color after being freshly cut, but it soon tarnishes to a dull grayish color when exposed...
, Silver
Silver
Silver is a metallic chemical element with the chemical symbol Ag and atomic number 47. A soft, white, lustrous transition metal, it has the highest electrical conductivity of any element and the highest thermal conductivity of any metal...
, Copper
Copper
Copper is a chemical element with the symbol Cu and atomic number 29. It is a ductile metal with very high thermal and electrical conductivity. Pure copper is soft and malleable; an exposed surface has a reddish-orange tarnish...
, Iron
Iron
Iron is a chemical element with the symbol Fe and atomic number 26. It is a metal in the first transition series. It is the most common element forming the planet Earth as a whole, forming much of Earth's outer and inner core. It is the fourth most common element in the Earth's crust...
, Tin
Tin
Tin is a chemical element with the symbol Sn and atomic number 50. It is a main group metal in group 14 of the periodic table. Tin shows chemical similarity to both neighboring group 14 elements, germanium and lead and has two possible oxidation states, +2 and the slightly more stable +4...
, Marble
Marble
Marble is a metamorphic rock composed of recrystallized carbonate minerals, most commonly calcite or dolomite.Geologists use the term "marble" to refer to metamorphosed limestone; however stonemasons use the term more broadly to encompass unmetamorphosed limestone.Marble is commonly used for...
, and Stone
Rock (geology)
In geology, rock or stone is a naturally occurring solid aggregate of minerals and/or mineraloids.The Earth's outer solid layer, the lithosphere, is made of rock. In general rocks are of three types, namely, igneous, sedimentary, and metamorphic...
). From these you can get the ratios and differences of specific weight
Specific weight
The specific weight is the weight per unit volume of a material. The symbol of specific weight is γ ....
found between the materials. With the instrument set at any opening, the intervals between any correspondingly marked pair of points will give the diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
s of balls (or sides of other solid bodies) similar to one another and equal in weight.
The Polygraphic Lines
From the given information, the side length and the number of sides, the Polygraphic lines yield the radius of the circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
that will contain the required regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
. If the polygon required has n sides, then the central angle opposite one side will be 360/n.
The Tetragonic Lines
Tetragonic Lines are so called from their principal use, which is to square all regular areas and the circle as well. The divisions of this scale use the function: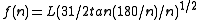
, between the values of 3 and 13.The Added Lines
These Added Lines are marked with two series of numbers, of which the outer series begins at a certain mark called D followed by the numbers 1, 2, 3, 4, and so on out to 18. The inner series begins from this mark D, going on then to 1, 2, 3, 4, and so on, also out to 18. They were used in conjunction with the other scales for a number of complex calculations.Use
The instrument can be used to graphically solve questions of proportion, and relies on the principle of similar triangles. Its vital feature is a pair of jointed legs, which carry paired geometrical scales. In use, problems are set up using a pair of dividers to determine the appropriate opening of the jointed legs and the answer is taken off directly as a dimension using the dividers. Specialised scales for area, volume and trigonometrical calculations, as well as simpler arithmetical problems were quickly added to the basic design.Different versions of the instrument also took different forms and adopted additional features. The type publicised by Hood was intended for use as a surveying instrument, and included not only sights and a mounting socket for attaching the instrument to a pole or post, but also an arc scale and an additional sliding leg. Galileo's earliest examples were intended to be used as gunner's levels as well as calculating devices.
The sector was a very useful instrument at a time when artisans and military men were poorly educated in mathematics and, often, were unable to perform even elementary arithmetical operations. The inaccuracy induced by the analog scales of the sector were usually of no concern to those attempting to find a rapid solution to an approximate problem. It is striking, however, that the disciplines to which these instruments were applied, particularly perspective, music, architecture and fortification, traditionally classed as mechanical sciences, soon emerged as mathematical sciences in the seventeenth century. Indeed there is evidence that the universality of these practical
applications helped to make possible the universality of science at a theoretical level. Hence this technology was not simply a consequence of advances in science. Rather, the technology helped make possible the mathematical sciences that led to modern science.