
Segre class
Encyclopedia
In mathematics
, the Segre class is a characteristic class
used in the study of singular vector bundle
s. The total Segre class is inverse to the total Chern class
, and thus provides equivalent information; the advantage of the Segre class is that it generalizes to singular vector bundles, while the Chern class does not.
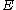 over a complex manifold
over a complex manifold 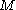 a total Segre class
a total Segre class 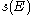 is the inverse to the total Chern class
is the inverse to the total Chern class
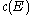 , see e.g. .
, see e.g. .
Explicitly, for a total Chern class
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Segre class is a characteristic class
Characteristic class
In mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
used in the study of singular vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s. The total Segre class is inverse to the total Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
, and thus provides equivalent information; the advantage of the Segre class is that it generalizes to singular vector bundles, while the Chern class does not.
Definition
For a holomorphic vector bundle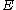 over a complex manifold
over a complex manifold 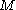 a total Segre class
a total Segre class 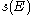 is the inverse to the total Chern class
is the inverse to the total Chern classChern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
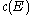 , see e.g. .
, see e.g. .Explicitly, for a total Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
-
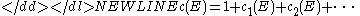
one gets the total Segre class
-
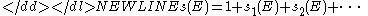
where
-
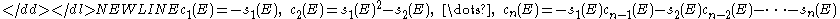
Let be Chern roots, i.e. formal eigenvalues of
be Chern roots, i.e. formal eigenvalues of  where
where 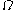 is a curvature of a connection on
is a curvature of a connection on 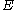 .
.
While the Chern class s(E) is written as
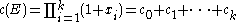
where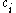 is an elementary symmetric polynomialElementary symmetric polynomialIn mathematics, specifically in commutative algebra, the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial P can be expressed as a polynomial in elementary symmetric polynomials: P can be given by an...
is an elementary symmetric polynomialElementary symmetric polynomialIn mathematics, specifically in commutative algebra, the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial P can be expressed as a polynomial in elementary symmetric polynomials: P can be given by an...
of degree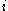 in variables
in variables 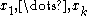
the Segre for the dual bundle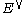 which has Chern roots
which has Chern roots 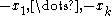 is written as
is written as
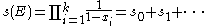
Expanding the above expression in powers of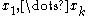 one can see that
one can see that 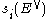 is represented by
is represented by
a complete homogeneous symmetric polynomialComplete homogeneous symmetric polynomialIn mathematics, specifically in algebraic combinatorics and commutative algebra, the complete homogeneous symmetric polynomials are a specific kind of symmetric polynomials...
of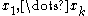
-
-

