Selberg's conjecture
Encyclopedia
In mathematics, the Selberg conjecture, named after Atle Selberg
, is about the density of zeros of the Riemann zeta function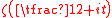
. It is known that the function has infinitely many zeroes on this line in the complex plane: the point at issue is how densely they are clustered. Results on this can be formulated in terms of N(T), the function counting zeroes on the line for which the value of t satisfies 0 ≤ t ≤ T.
; and he proved that for any
there exist
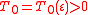
and
such that for
and
the inequality
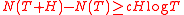
holds true.
In his turn, Selberg stated a conjecture relating to shorter intervals, namely that it is possible to decrease the value of the exponent
in
.
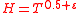proved that for a fixed
satisfying the condition
a sufficiently large
and
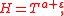
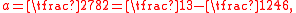
the interval in the ordinate t
contains at least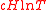 
real zeros of the Riemann zeta function
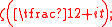
and thereby confirmed the Selberg conjecture. The estimates of Selberg and Karatsuba cannot be improved in respect of the order of growth as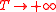
.
, 
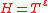, where 
is an arbitrarily small fixed positive number. The Karatsuba method permits one to investigate zeroes of the Riemann zeta-function on "supershort" intervals of the critical line, that is, on the intervals 
, the length 
of which grows slower than any, even arbitrarily small degree 
.
In particular, he proved that for any given numbers
, 
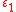satisfying the conditions 
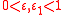almost all intervals 
for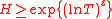 
contain at least 
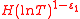zeros of the function 
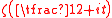. This estimate is quite close to the conditional result that follows from the Riemann hypothesis
.
Atle Selberg
Atle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
, is about the density of zeros of the Riemann zeta function
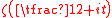. It is known that the function has infinitely many zeroes on this line in the complex plane: the point at issue is how densely they are clustered. Results on this can be formulated in terms of N(T), the function counting zeroes on the line for which the value of t satisfies 0 ≤ t ≤ T.Background
In 1942 Atle Selberg investigated the problem of the Hardy–Littlewood conjecture 2Hardy–Littlewood zeta-function conjectures
In mathematics, the Hardy–Littlewood zeta-function conjectures, named after Godfrey Harold Hardy and John Edensor Littlewood, are two conjectures concerning the distances between zeros and the density of zeros of the Riemann zeta function....
; and he proved that for any
there exist
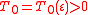
and
such that for
and
the inequality
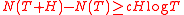
holds true.
In his turn, Selberg stated a conjecture relating to shorter intervals, namely that it is possible to decrease the value of the exponent
in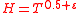.Proof of the conjecture
In 1984 Anatolii Alexeevitch KaratsubaAnatolii Alexeevitch Karatsuba
Anatolii Alexeevitch Karatsuba was a Russian mathematician, who authored the first fast multiplication method: the Karatsuba algorithm, a fast procedure for multiplying large numbers.- Studies and work :...
proved that for a fixed
satisfying the conditiona sufficiently large
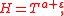
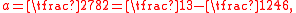
and the interval in the ordinate t
contains at least 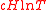real zeros of the Riemann zeta function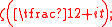and thereby confirmed the Selberg conjecture. The estimates of Selberg and Karatsuba cannot be improved in respect of the order of growth as
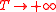.Further work
In 1992 Karatsuba proved that an analog of the Selberg conjecture holds for "almost all" intervals, , 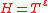where is an arbitrarily small fixed positive number. The Karatsuba method permits one to investigate zeroes of the Riemann zeta-function on "supershort" intervals of the critical line, that is, on the intervals , the length of which grows slower than any, even arbitrarily small degree .In particular, he proved that for any given numbers
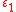, satisfying the conditions 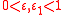almost all intervals for 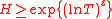contain at least 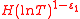zeros of the function 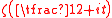. This estimate is quite close to the conditional result that follows from the Riemann hypothesisRiemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
.