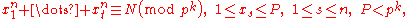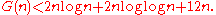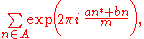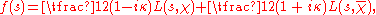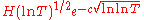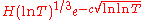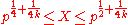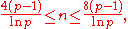Anatolii Alexeevitch Karatsuba
Encyclopedia
Anatolii Alexeevitch Karatsuba ' onMouseout='HidePop("26525")' href="/topics/Grozny">Grozny
, January 31, 1937 — Moscow
, September 28, 2008) was a Russian mathematician
, who authored the first fast multiplication method: the Karatsuba algorithm, a fast procedure for multiplying large numbers
.
In 1959, he graduated from Lomonosov Moscow State University, Department of Mathematics and Mechanics. In 1962 he got his PhD degree Candidate of Sciences in Physics and Mathematics, thesis «Rational trigonometric sums of special kind and their applications» (PhD supervisor N.M.Korobov), and started to work at the department of Mathematics and Mechanics of MSU. In 1966 he got his Habilitation (Doctor of Sciences in Physics and
Mathematics degree), with the thesis «The method of trigonometric sums and the mean value theorems» and became a member of
Steklov Institute of Mathematics
(MIAN).
After 1983, he was a leading researcher in Number theory
in the USSR and Russia. He was Head of Division of Number Theory in the Steklov Institute, Professor of the Division for Number Theory at Moscow State University since 1970 and Professor of Division for Mathematical analysis
of Moscow State University since 1980. His research interests included Trigonometric series and Trigonometric integrals, the Riemann zeta function,
Dirichlet characters, Finite-state machines, effective Algorithm
s.
Karatsuba supervised the PhD studies of 15 students who obtained their PhD degrees (Cand. of Science); seven of them later obtained the second Habilitation degree (Doctor of Sciences). Karatsuba was awarded state prizes and honorary titles.
and found solutions to two problems set up by Kolmogorov. This was essential for the development of automata theory and started a new branch in Mathematics, the theory of fast algorithms.
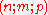, an automat (or a machine) 
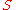, is defined as a device with 
states, 
input symbols
and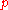
output symbols. Nine theorems on the structure of 
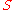and experiments with 
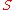are proved. Later such 
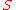machines got the name of Moore machine
s. At the end of the paper, in the chapter «New problems», Moore formulates the problem of improving the estimates which he obtained in Theorems 8 and 9:
In 1957 Karatsuba proved two theorems which completely solved the Moore problem on improving the estimate of the length of experiment in his Theorem 8.
These two theorems were proved by Karatsuba in his 4th year as a basis of his 4th year project; the corresponding paper was submitted to the journal "Uspekhi Mat. Nauk" on December 17, 1958 and published in June 1960. Up to this day (2011) this result of Karatsuba that later acquired the title "the Moore-Karatsuba theorem", remains the only precise (the only precise non-linear order of the estimate) non-linear result both in the automata theory and in the similar problems of the theory of complexity of computations.
Andrey Kolmogorov
was the first who set up problems on the bit complexity of computations. The complexity of multiplication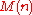
is defined as the number of bit operations sufficient to calculate the product of two 
-digit numbers by means of the given algorithm.
Multiplying two
-digit integers by the usual school method "in a column", we obtain the upper bound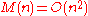 
. In 1956 A.N.Kolmogorov conjectured that the lower bound for 
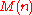for any method of multiplication is also of the order 
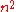, that is, it is impossible to calculate the product of two 
-digit integers faster than by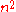 
operations (the so called ``Kolmogorov
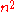conjecture). The 
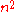conjecture seemed realistic, because in all the previous history people multiplied numbers with the complexity of order 
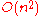, and if a faster method of multiplication existed then in all probability it would have been already
discovered.
In 1960, Anatolii Karatsuba found a new method of multiplication of two
-digit numbers, now known as the Karatsuba algorithm,
for which the order of complexity is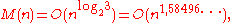
thus disproving the 
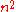conjecture. This result was explained by Karatsuba at the Kolmogorov seminar at Moscow State University in 1960, after which that Kolmogorov's seminar came to an end. The first paper describing the method was prepared by Kolmogorov himself, where he presented two different and not connected with each other results of two of his students. In the paper Kolmogorov clearly specified that one theorem (not dealing with fast multiplication) belongs to Yu.Ofman and another one (with the first ever fast multiplication algorithm) belongs to A. Karatsuba. The Karatsuba method was later named «Divide and conquer algorithm». The other names of this method, depending on the area of its application, are Binary Splitting, the Dichotomy Principle etc.
Later on the basis of Karatsuba's idea thousands of fast algorithms were constructed, of which the most known are its direct generalizations, such as Schönhage–Strassen algorithm, the Strassen algorithm
of matrix multiplication and the Fast Fourier transform
(see also the Cooley–Tukey FFT algorithm). In recent years, the title Divide and Conquer is used for operations that break a problem into parts, and this is no longer always connected with fast computational algorithms.
A French mathematician and philosopher :fr:Jean-Paul Delahaye referred to the Karatsuba method of multiplication as the «one of the most useful results of mathematics».
The algorithm of Anatolii Karatsuba is implemented in practically all modern computers, not only as software, but as hardware as well.
"When describing the works of outstanding scientists, it is natural to emphasize some characteristic and special features of their creative work. Such distinguishing features of Professor Karatsuba's scientific work are combinatorial ingenuity, fundamental character and certain completeness of results."
The main research works of A.A.Karatsuba were published in more than 160 research papers and monographs.
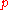-adic method in the theory of trigonometric sums. The estimates of so-called 
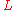-sums of the form
led to the new bounds for zeros of the Dirichlet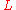
-series modulo a power of a prime number, to the asymptotic formula for the number of Waring congruence of the form
to a solution of the problem of distribution of fractional parts of a polynomial with integer coefficients modulo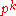
. A.A. Karatsuba was the first to realize in the 
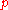-adic form the «embedding principle» of Euler-Vinogradov and to compute a 
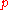-adic analog of Vinogradov 
-numbers when estimating the number of solutions of a congruence of the Waring type.
Assume that :
and moreover :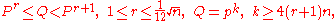 
where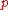 
is a prime number. Karatsuba proved that in that case for any natural number 
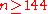there exists a 
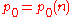such that for any 
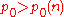every natural number 
can be represented in the form (1) for 
, and for 
there exist 
such that the congruence (1) has no solutions.
This new approach, found by Karatsuba, led to a new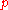
-adic proof of the Vinogradov mean value theorem, which plays the central part in the Vinogradov's method of trigonometric sums.
Another component of the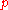
-adic method of A.A. Karatsuba is the transition from incomplete systems of equations to complete ones at the expense of the local 
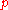-adic change of unknowns.
Let
be an arbitrary natural number, 
. Determine an integer 
by the inequalities 
. Consider the system of equations
Grozny
Grozny is the capital city of the Chechen Republic, Russia. The city lies on the Sunzha River. According to the preliminary results of the 2010 Census, the city had a population of 271,596; up from 210,720 recorded in the 2002 Census. but still only about two-thirds of 399,688 recorded in the 1989...
, January 31, 1937 — Moscow
Moscow
Moscow is the capital, the most populous city, and the most populous federal subject of Russia. The city is a major political, economic, cultural, scientific, religious, financial, educational, and transportation centre of Russia and the continent...
, September 28, 2008) was a Russian mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, who authored the first fast multiplication method: the Karatsuba algorithm, a fast procedure for multiplying large numbers
Multiplication algorithm
A multiplication algorithm is an algorithm to multiply two numbers. Depending on the size of the numbers, different algorithms are in use...
.
Studies and work
From 1944-1954, Anatolii Karatsuba studied at the high school № 6 for boys of the city of Grozny and completed his studies with a silver medal. Already in his early years he showed exceptional talents in mathematics, being a young student he solved problems that were given to the students of the last years at school as a challenge.In 1959, he graduated from Lomonosov Moscow State University, Department of Mathematics and Mechanics. In 1962 he got his PhD degree Candidate of Sciences in Physics and Mathematics, thesis «Rational trigonometric sums of special kind and their applications» (PhD supervisor N.M.Korobov), and started to work at the department of Mathematics and Mechanics of MSU. In 1966 he got his Habilitation (Doctor of Sciences in Physics and
Mathematics degree), with the thesis «The method of trigonometric sums and the mean value theorems» and became a member of
Steklov Institute of Mathematics
Steklov Institute of Mathematics
Steklov Institute of Mathematics or Steklov Mathematical Institute is a research institute based in Moscow, specialized in mathematics, and a part of the Russian Academy of Sciences. It was established April 24, 1934 by the decision of the General Assembly of the Academy of Sciences of the USSR in...
(MIAN).
After 1983, he was a leading researcher in Number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
in the USSR and Russia. He was Head of Division of Number Theory in the Steklov Institute, Professor of the Division for Number Theory at Moscow State University since 1970 and Professor of Division for Mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
of Moscow State University since 1980. His research interests included Trigonometric series and Trigonometric integrals, the Riemann zeta function,
Dirichlet characters, Finite-state machines, effective Algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s.
Karatsuba supervised the PhD studies of 15 students who obtained their PhD degrees (Cand. of Science); seven of them later obtained the second Habilitation degree (Doctor of Sciences). Karatsuba was awarded state prizes and honorary titles.
Awards and Titles
- 19811981 in scienceThe year 1981 in science and technology involved many significant events, listed below.-Medicine:* June 5 - AIDS pandemic begins when the United States Centers for Disease Control and Prevention reports an unusual cluster of Pneumocystis pneumonia in five homosexual men in Los Angeles.* Dr Bruce...
: P.L.Tchebyshev Prize of Soviet Academy of Sciences - 19991999 in scienceThe year 1999 in science and technology involved some significant events.-Aeronautics:* February 27 – While trying to circumnavigate the world in a hot air balloon, Colin Prescot and Andy Elson set a new endurance record after being in a hot air balloon for 233 hours and 55 minutes.* March 3 –...
: Distinguished Scientist of Russia - 20012001 in scienceThe year 2001 in science and technology involved many events, some of which are included below.-Astronomy and space exploration:* The NEAR Shoemaker spacecraft lands in the "saddle" region of 433 Eros, becoming the first spacecraft to land on an asteroid....
: I.M.Vinogradov Prize of Russian Academy of Sciences
The early works on Informatics
As a student of Lomonosov Moscow State University, Karatsuba attended the seminar of Andrey KolmogorovAndrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
and found solutions to two problems set up by Kolmogorov. This was essential for the development of automata theory and started a new branch in Mathematics, the theory of fast algorithms.
Automata
In the paper of :Edward F. Moore,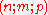, an automat (or a machine) 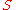, is defined as a device with states, input symbolsand
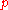output symbols. Nine theorems on the structure of 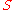and experiments with 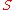are proved. Later such 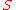machines got the name of Moore machineMoore machine
In the theory of computation, a Moore machine is a finite-state machine, whose output values are determined solely by its current state.-Name:The Moore machine is named after Edward F...
s. At the end of the paper, in the chapter «New problems», Moore formulates the problem of improving the estimates which he obtained in Theorems 8 and 9:
- Theorem 8 (Moore). Given an arbitrary
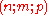machine 
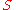, such that every two states can be distinguished from each other, there exists an experiment of length 
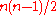that identifies the state of 
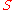at the end of this experiment.
In 1957 Karatsuba proved two theorems which completely solved the Moore problem on improving the estimate of the length of experiment in his Theorem 8.
- Theorem A (Karatsuba). If
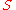is a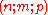 
machine such that each two its states can be distinguished from each other then there exists a ramified experiment of length at most , by means of which one can find the state 
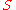at the end of the experiment.
- Theorem B (Karatsuba). There exists a
machine, every states of which can be distinguished from each other, such that the length of the shortest experiment finding the state of the machine at the end of the experiment, is equal to .
These two theorems were proved by Karatsuba in his 4th year as a basis of his 4th year project; the corresponding paper was submitted to the journal "Uspekhi Mat. Nauk" on December 17, 1958 and published in June 1960. Up to this day (2011) this result of Karatsuba that later acquired the title "the Moore-Karatsuba theorem", remains the only precise (the only precise non-linear order of the estimate) non-linear result both in the automata theory and in the similar problems of the theory of complexity of computations.
Fast algorithms
Fast algorithms is the area of computational mathematics that studies algorithms of computing a given function with a given precision using the least possible number of bit operations. Assuming that the numbers are written in the binary system, the signs 0 and 1 of which are called "bits". One "bit operation" is defined as writing down one of the signs 0, 1, plus, minus, bracket; putting together, subtracting and multiplying two bits.Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
was the first who set up problems on the bit complexity of computations. The complexity of multiplication
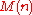is defined as the number of bit operations sufficient to calculate the product of two -digit numbers by means of the given algorithm.Multiplying two
-digit integers by the usual school method "in a column", we obtain the upper bound 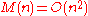. In 1956 A.N.Kolmogorov conjectured that the lower bound for 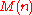for any method of multiplication is also of the order 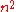, that is, it is impossible to calculate the product of two -digit integers faster than by 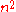operations (the so called ``Kolmogorov 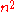conjecture). The 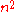conjecture seemed realistic, because in all the previous history people multiplied numbers with the complexity of order 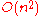, and if a faster method of multiplication existed then in all probability it would have been alreadydiscovered.
In 1960, Anatolii Karatsuba found a new method of multiplication of two
-digit numbers, now known as the Karatsuba algorithm,for which the order of complexity is
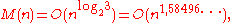thus disproving the 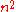conjecture. This result was explained by Karatsuba at the Kolmogorov seminar at Moscow State University in 1960, after which that Kolmogorov's seminar came to an end. The first paper describing the method was prepared by Kolmogorov himself, where he presented two different and not connected with each other results of two of his students. In the paper Kolmogorov clearly specified that one theorem (not dealing with fast multiplication) belongs to Yu.Ofman and another one (with the first ever fast multiplication algorithm) belongs to A. Karatsuba. The Karatsuba method was later named «Divide and conquer algorithm». The other names of this method, depending on the area of its application, are Binary Splitting, the Dichotomy Principle etc.Later on the basis of Karatsuba's idea thousands of fast algorithms were constructed, of which the most known are its direct generalizations, such as Schönhage–Strassen algorithm, the Strassen algorithm
Strassen algorithm
In the mathematical discipline of linear algebra, the Strassen algorithm, named after Volker Strassen, is an algorithm used for matrix multiplication...
of matrix multiplication and the Fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(see also the Cooley–Tukey FFT algorithm). In recent years, the title Divide and Conquer is used for operations that break a problem into parts, and this is no longer always connected with fast computational algorithms.
A French mathematician and philosopher :fr:Jean-Paul Delahaye referred to the Karatsuba method of multiplication as the «one of the most useful results of mathematics».
The algorithm of Anatolii Karatsuba is implemented in practically all modern computers, not only as software, but as hardware as well.
Works in Number Theory
In the paper «On the mathematical works of Professor A.A. Karatsuba», published on the occasion of the 60th birthday of A.A. Karatsuba, his former students G.I. Arkhipov and V.N. Chubarikov characterize the special features of A.A.Karatsuba's research papers in the following way:"When describing the works of outstanding scientists, it is natural to emphasize some characteristic and special features of their creative work. Such distinguishing features of Professor Karatsuba's scientific work are combinatorial ingenuity, fundamental character and certain completeness of results."
The main research works of A.A.Karatsuba were published in more than 160 research papers and monographs.
The
p-adic method A.A.Karatsuba constructed a new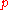-adic method in the theory of trigonometric sums. The estimates of so-called 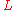-sums of the form
led to the new bounds for zeros of the Dirichlet
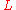-series modulo a power of a prime number, to the asymptotic formula for the number of Waring congruence of the form
to a solution of the problem of distribution of fractional parts of a polynomial with integer coefficients modulo
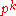. A.A. Karatsuba was the first to realize in the 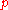-adic form the «embedding principle» of Euler-Vinogradov and to compute a 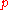-adic analog of Vinogradov -numbers when estimating the number of solutions of a congruence of the Waring type.Assume that :
and moreover : 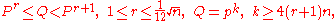where 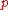is a prime number. Karatsuba proved that in that case for any natural number 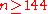there exists a 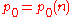such that for any 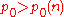every natural number can be represented in the form (1) for , and for there exist such that the congruence (1) has no solutions.This new approach, found by Karatsuba, led to a new
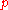-adic proof of the Vinogradov mean value theorem, which plays the central part in the Vinogradov's method of trigonometric sums.Another component of the
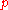-adic method of A.A. Karatsuba is the transition from incomplete systems of equations to complete ones at the expense of the local 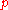-adic change of unknowns.Let
be an arbitrary natural number, . Determine an integer by the inequalities . Consider the system of equations-
Karatsuba proved that the number of solutions
of this system of equations for 
satisfies the estimate
For incomplete systems of equations, in which the variables run through numbers with small prime divisors, Karatsuba applied multiplicative translation of variables. This led to an essentially new estimate of trigonometric sums and a new mean value theorem for such systems of equations.
The Hua Luogeng problem on the convergency exponent of the singular integral in the Terry problem
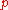-adic method of A.A.Karatsuba includes the techniques of estimating the measure of the set of points with small values of functions in terms of the values of their parameters (coefficients etc.) and, conversely, the techniques of estimating those parameters in terms of the measure of this set in the real and 
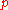-adic metrics. This side of Karatsuba's method manifested itself especially clear in estimating trigonometric integrals, which led to the solution of the problem of Hua LuogengHua LuogengHua Luogeng was a Chinese mathematician born in Jintan, Jiangsu. He was the founder and pioneer in many fields in mathematical research. He wrote more than 200 papers and monographs, many of which became classics. Since his sudden death while delivering a lecture at the University of Tokyo, Japan,...
. In 1979 Karatsuba, together with his students G.I. Arkhipov and V.N. Chubarikov obtained a complete solution of the Hua Luogeng problem of finding the exponent of convergency of the integral:
-
where
is a fixed number.
The problem was set up in 1937.
In this case, the exponent of convergency means the value
, such that 
converges for 
and diverges for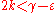 
, where 
is arbitrarily small. It was shown that the integral 
converges for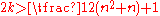 
and diverges for
.
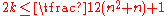At the same time, the similar problem for the integral was solved:
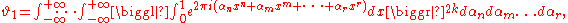
where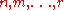
are integers, satisfying the conditions : 
Karatsuba and his students proved that the integral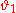
converges, if 
and diverges, if 
.
The integrals
and 
arise in the studying of the so called Prouhet–Tarry–Escott problem. Karatsuba and his students obtained a series of new results connected with the multi-dimensional analog of the Tarry problem. In particular, they proved that if 
is a polynomial in 
variables (
) of the form :
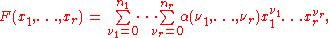
with the zero free term,
, 
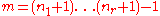is
the
-dimensional vector, consisting of the coefficients of 
, then the integral :
converges for 
, where 
is the highest of the numbers 
. This result, being not a final one, generated a new area in the theory of trigonometric integrals, connected with improving the bounds of the exponent of convergency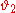 
(I. A. Ikromov, M. A. Chahkiev and others).
Multiple trigonometric sums
In 1966—1980, Karatsuba developed (with participation of his students G.I. Arkhipov and V.N. Chubarikov) the theory of multiple Hermann WeylHermann WeylHermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
trigonometric sums, that is, the sums of the form
-
, where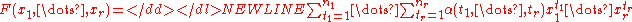 
,
is a system of real coefficients 
. The central point of that theory, as in the theory of the Vinogradov trigonometric sums, is the following mean value theorem.
- Let
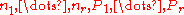be natural numbers, 
,
. Furthermore, let 
be the 
-dimensional cube of the form :: 
, 
, in the euclidean space : and ::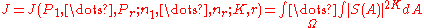 
. : Then for any 
and 
the value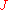 
can be estimated as follows
-
, :
-
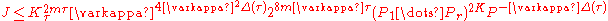where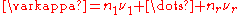
, 
, 
, 
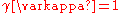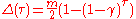, and the natural numbers 
are such that: :: 
, 
.
The mean value theorem and the lemma on the multiplicity of intersection of multi-dimensional parallelepipeds form the basis of the estimate of a multiple trigonometric sum, that was obtained by Karatsuba (two-dimensional case was derived by G.I. Arkhipov). Denoting by
the least common multiple of the numbers 
with the condition 
, for 
the estimate holds
-
,
where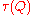
is the number of divisors of the integer 
, and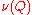 
is the number of distinct prime divisors of the number 
.
The estimate of the Hardy function in the Waring problem
Applying his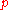
-adic form of the Hardy-Littlewood-Ramanujan-Vinogradov method to estimating trigonometric sums, in which the summation is taken over numbers with small prime divisors, Karatsuba obtained a new estimate of the well known HardyG. H. HardyGodfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
function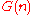
in the Waring's problemWaring's problemIn number theory, Waring's problem, proposed in 1770 by Edward Waring, asks whether for every natural number k there exists an associated positive integer s such that every natural number is the sum of at most s kth powers of natural numbers...
(for
):
Multi-dimensional analog of the Waring problem
In his subsequent investigation of the Waring problem Karatsuba obtained the following two-dimensional generalization of that problem:
Consider the system of equations
-
, 
,
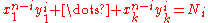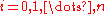where
are given positive integers with the same order or growth, 
, and 
are unknowns, which are also positive integers. This system has solutions, if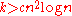 
, and if 
, then there exist such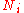 
, that the system has no solutions.
The Artin problem of local representation of zero by a form
Emil ArtinEmil ArtinEmil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
had posed the problem on the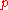
-adic representation of zero by a form of arbitrary degree d. Artin initially conjectured a result, which would now be described as the p-adic field being a C2 fieldQuasi-algebraically closed fieldIn mathematics, a field F is called quasi-algebraically closed if every non-constant homogeneous polynomial P over F has a non-trivial zero provided the number of its variables is more than its degree....
; in other words non-trivial representation of zero would occur if the number of variables was at least d2. This was shown not to be the case by an example of Guy TerjanianGuy TerjanianGuy Terjanian is a French-Armenian mathematician who has worked on algebraic number theory. He achieved his Ph.D under Claude Chevalley in 1966, and at that time published a counterexample to the original form of a conjecture of Emil Artin, which suitably modified had just been proved as the...
. Karatsuba showed that, in order to have a non-trivial representation of zero by a form, the number of variables should grow faster than polynomially in the degree d; this number in fact should have an almost exponential growth, depending on the degree. Karatsuba and his student Arkhipov proved, that for any natural number
there exists 
, such that for any 
there is a form with integral coefficients 
of degree smaller than 
, the number of variables of which is 
, 
,
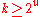which has only trivial representation of zero in the 2-adic numbers. They also obtained a similar result for any odd prime modulus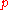
.
Estimates of short Kloosterman sums
Karatsuba developed (1993—1999) a new method of estimating short
Kloosterman sums, that is, trigonometric sums of the form
where
runs through a set 
of numbers, coprime to 
, the number of elements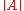 
in which is essentially smaller than 
, and the symbol 
denotes the congruence class, inverse to 
modulo 
: 
.
Up to the early 1990s, the estimates of this type were known, mainly, for sums in which the number of summands was higher than
(H. D. KloostermanHendrik KloostermanHendrik Douwe Kloosterman was a Dutch mathematician, known for his work in number theory and in representation theory....
, I. M. VinogradovIvan Matveyevich VinogradovIvan Matveevich Vinogradov was a Soviet mathematician, who was one of the creators of modern analytic number theory, and also a dominant figure in mathematics in the USSR. He was born in the Velikiye Luki district, Pskov Oblast. He graduated from the University of St...
, H. Salié,
L. CarlitzLeonard CarlitzLeonard Carlitz was an American mathematician. Carlitz supervised 44 Doctorates at Duke University and published over 770 papers.- Chronology :* 1907 Born Philadelphia, PA, USA* 1927 BA, University of Pennsylvania...
, S. Uchiyama, A. WeilAndré WeilAndré Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
). The only exception was the special moduli of the form
, where 
is a fixed prime and the exponent 
increases to infinity (this case was studied by A. G. Postnikov by means of the method of Vinogradov). Karatsuba's method makes it possible to estimate Kloosterman sums where the number of summands does not exceed
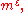
and in some cases even
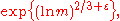
where
is an arbitrarily small fixed number. The final paper of Karatsuba on this subject was published posthumously.
Various aspects of the method of Karatsuba have found applications in the following problems of analytic number theory:
- finding asymptotics of the sums of fractional parts of the form :
: where 
runs, one after another, through the integers satisfying the condition 
, and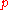 
runs through the primes that do not divide the module 
(Karatsuba);
- finding a lower bound for the number of solutions of inequalities of the form :
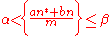: in the integers 
, 
, coprime to 
, 
(Karatsuba);
- the precision of approximation of an arbitrary real number in the segment
by fractional parts of the form :
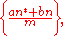: where 
, 
, 
(Karatsuba);
- a more precise constant
in the Brun–Titchmarsh theoremBrun–Titchmarsh theoremIn analytic number theory, the Brun–Titchmarsh theorem, named after Viggo Brun and Edward Charles Titchmarsh, is an upper bound on the distribution of prime numbers in arithmetic progression...
:
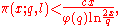: where 
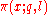is the number of primes 
, not exceeding 
and belonging to the arithmetic progression 
(J. FriedlanderJohn FriedlanderJohn Benjamin Friedlander is a Canadian mathematician specializing in analytic number theory. He received his B.Sc. from the University of Toronto in 1965, an M.A. from the University of Waterloo in 1966, and a Ph.D. from Pennsylvania State University in 1972. He was a lecturer at M.I.T...
, H. IwaniecHenryk IwaniecHenryk Iwaniec is a Polish American mathematician, and since 1987 a professor at Rutgers University. He was awarded the fourteenth Frank Nelson Cole Prize in Number Theory in 2002. He received the Leroy P. Steele Prize for Mathematical Exposition in 2011.-Background and education:Iwaniec studied...
);
- a lower bound for the greatest prime divisor of the product of numbers of the form :
, 
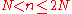
(D. R. Heath-BrownRoger Heath-BrownDavid Rodney "Roger" Heath-Brown F.R.S. , is a British mathematician working in the field of analytic number theory. He was an undergraduate and graduate student of Trinity College, Cambridge; his research supervisor was Alan Baker...
);
- proving that there are infinitely many primes of the form:
(J. FriedlanderJohn FriedlanderJohn Benjamin Friedlander is a Canadian mathematician specializing in analytic number theory. He received his B.Sc. from the University of Toronto in 1965, an M.A. from the University of Waterloo in 1966, and a Ph.D. from Pennsylvania State University in 1972. He was a lecturer at M.I.T...
, H. IwaniecHenryk IwaniecHenryk Iwaniec is a Polish American mathematician, and since 1987 a professor at Rutgers University. He was awarded the fourteenth Frank Nelson Cole Prize in Number Theory in 2002. He received the Leroy P. Steele Prize for Mathematical Exposition in 2011.-Background and education:Iwaniec studied...
);
- combinatorial properties of the set of numbers :
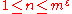
(A. A. Glibichuk).
The Selberg conjecture
In 1984 Karatsuba proved, that for a fixed
satisfying the condition
, a sufficiently large 
and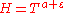 
, 
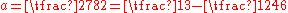, the interval 
contains at least 
real zeros of the Riemann zeta function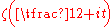 
.
This claim was conjectured in 1942 by Atle SelbergAtle SelbergAtle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
, who proved it himself for the case
. The estimates of Atle SelbergAtle SelbergAtle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
and Karatsuba can not be improved in respect of the order of growth as
.
Distribution of zeros of the Riemann zeta function on the short intervals of the critical line
Karatsuba also obtained a number of results about the distribution of zeros of
on «short» intervals of the critical line. He proved that an analog of the Selberg conjecture holds for «almost all» intervals 
, 
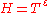, where 
is an arbitrarily small fixed positive number. Karatsuba developed (1992) a new approach to investigating zeros of the Riemann zeta-function on «supershort» intervals of the critical line, that is, on the intervals 
, the length 
of which grows slower than any, even arbitrarily small degree 
. In particular, he proved that for any given numbers 
, 
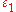satisfying the conditions 
almost all intervals 
for 
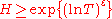contain at least 
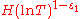zeros of the function 
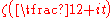. This estimate is quite close to the one that follows from the Riemann hypothesisRiemann hypothesisIn mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
.
Zeros of linear combinations of Dirichlet L-series
Karatsuba developed a new method of investigating zeros of functions which can be represented as linear combinations of Dirichlet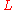
-series. The simplest example of a function of that type is the Davenport-Heilbronn function, defined by the equality
where
is a non-principal character modulo 
(
, 
, 
, 
, 
, 
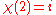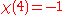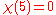for any 
),
For
Riemann hypothesisRiemann hypothesisIn mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
is not true, however, the critical line
contains, nevertheless, anormally many zeros.
Karatsuba proved (1989) that the interval
, 
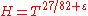, contains at least
zeros of the function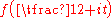
. Similar results were obtained by Karatsuba also for linear combinations containing arbitrary (finite) number of summands; the degree exponent 
is here replaced by a smaller number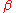 
, that depends only on the form of the linear combination.
The boundary of zeros of the zeta function and the multi-dimensional problem of Dirichlet divisors
To Karatsuba belongs a new breakthrough result in the multi-dimensional problem of Dirichlet divisors, which is connected with finding the number
of solutions of the inequality 
in the natural numbers 
as 
. For 
there is an asymptotic formula of the form
-
,
where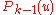
is a polynomial of degree 
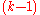, the coefficients of which depend on 
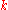and can be found explicitly and 
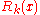is the remainder term, all known estimates of which (up to 1960) were of the form
-
,
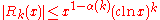where
, 
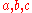are some absolute positive constants.
Karatsuba obtained a more precise estimate of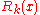
, in which the value 
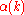was of order 
and was decreasing much slower than 
in the previous estimates. Karatsuba's estimate is uniform in 
and 
; in particular, the value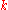 
may grow as 
grows (as some power of the logarithm of 
). (A similar looking, but weaker result was obtained in 1960 by a German mathematician Richert, whose paper remained unknown to Soviet mathematicians at least until the mid-seventies.)
Proof of the estimate of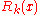
is based on a series of claims, essentially equivalent to the theorem on the boundary of zeros of the Riemann zeta function, obtained by the method of Vinogradov, that is, the theorem claiming that 
has no zeros in the region
-
.
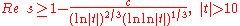Karatsuba found (2000) the backward relation of estimates of the values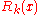
with the behaviour of
near the line 
. In particular, he proved that if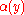 
is an arbitrary non-increasing function satisfying the condition 
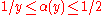, such that for all 
the estimate
holds, then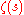
has no zeros in the region
(
are some absolute constants).
Estimates from below of the maximum of the modulus of the zeta function in small regions of the critical domain and on small intervals of the critical line
Karatsuba introduced and studied the functions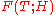
and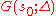 
, defined by the equalities
Here
is a sufficiently large positive number, 
, 
, 
, 
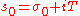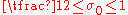. Estimating the values 
and 
from below shows, how large (in modulus) values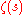 
can take on short intervals of the critical line or in small neighborhoods of points lying in the critical strip 
. The case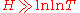 
was studied earlier by Ramachandra; the case 
, where 
is a sufficiently large constant, is trivial.
Karatsuba proved, in particular, that if the values
and 
exceed certain sufficiently small constants, then the estimates
hold, where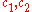
are certain absolute constants.
Behaviour of the argument of the zeta-function on the critical line
Karatsuba obtained a number of new results related to the behaviour of the function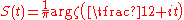
, which is called the argument of Riemann zeta function on the
critical line (here
is the increment of an arbitrary continuous branch of 
along the broken line joining the points 
and 
). Among those results are the mean value theorems for the function 
and its first integral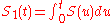 
on intervals of the real line, and also the theorem claiming that every interval 
for 
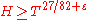contains at least
points where the function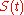
changes sign. Earlier similar results were obtained by Atle SelbergAtle SelbergAtle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
for the case
.
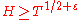Estimates of short sums of characters in finite fields
In the end of the sixties Karatsuba, estimating short sums of Dirichlet characterDirichlet characterIn number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
s, developed a new method, making it possible to obtain non-trivial estimates of short sums of characters in finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s. Let
be a fixed integer, 
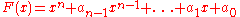a polynomial, irreducible over the field 
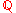of rational numbers, 
a root of the equation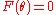 
, 
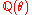the corresponding extension of the field 
, 
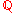a basis of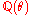 
, 
, 
, 
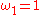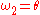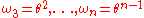. Furthermore, let 
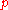be a sufficiently large prime, such that 
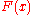is irreducible modulo 
,
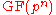the Galois fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with a basis
, 
a non-principal Dirichlet characterDirichlet characterIn number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
of the field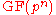
. Finally, let 
be some nonnegative integers,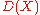 
the set of elements 
of the Galois field 
,
-
,
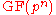such that for any
, 
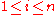, the following inequalities hold:
-
.
Karatsuba proved that for any fixed
, 
, and arbitrary 
satisfying the condition
the following estimate holds:
where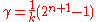
, and the constant 
depends only on 
and the basis 
.
Estimates of linear sums of characters over shifted prime numbers
Karatsuba developed a number of new tools, which, combined with the Vinogradov method of estimating sums with prime numbers, enabled him to obtain in 1970 an estimate of the sum of values of a non-principal character modulo a prime
on a sequence of shifted prime numbers, namely, an estimate of the form
where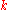
is an integer satisfying the condition 
, 
an arbitrarily small fixed number, 
, and the constant 
depends on 
only.
This claim is considerably stronger than the estimate of Vinogradov, which is non-trivial for
.
In 1971 speaking at the International conference on number theory on the occasion of the 80th birthday of Ivan Matveyevich VinogradovIvan Matveyevich VinogradovIvan Matveevich Vinogradov was a Soviet mathematician, who was one of the creators of modern analytic number theory, and also a dominant figure in mathematics in the USSR. He was born in the Velikiye Luki district, Pskov Oblast. He graduated from the University of St...
, Academician Yuri LinnikYuri LinnikYuri Vladimirovich Linnik was a Soviet mathematician active in number theory, probability theory and mathematical statistics.Linnik was born in Bila Tserkva, in present-day Ukraine. He went to St Petersburg University where his supervisor was Vladimir Tartakovski, and later worked at that...
noted the following:
«Of a great importance are the investigations carried out by Vinogradov in the area of asymptotics of Dirichlet characterDirichlet characterIn number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
on shifted primes
, which give a decreased power compared to 
compared to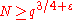 
,
, where 
is the modulus of the character. This estimate is of crucial importance, as it is so deep that gives more than the extended Riemann hypothesisRiemann hypothesisIn mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
, and, it seems, in that directions is a deeper fact than that conjecture (if the conjecture is true). Recently this estimate was improved by A.A.Karatsuba».
This result was extended by Karatsuba to the case when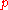
runs through the primes in an arithmetic progression, the increment of which grows with the modulus
.
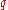Estimates of sums of characters on polynomials with a prime argument
Karatsuba found a number of estimates of sums of
Dirichlet characters in polynomials of degree two for the case when the argument of the polynomial runs through a short sequence of subsequent primes. Let, for instance,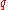
be a sufficiently high prime, 
, where 
and 
are integers, satisfying the condition 
, and let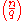 
denote the Legendre symbolLegendre symbolIn number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
, then for any fixed
with the condition 
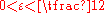and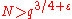 
for the sum 
,
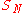the following estimate holds:
(here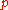
runs through subsequent primes, 
is the number of primes not exceeding 
, and 
is a constant, depending on 
only).
A similar estimate was obtained by Karatsuba also for the case when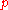
runs through a sequence of primes in an arithmetic progression, the increment of which may grow together with the modulus 
.
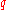Karatsuba conjectured that the non-trivial estimate of the sum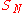
for 
, which are "small" compared to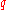 
, remains true in the case when 
is replaced by an arbitrary polynomial of degree 
, which is not a square modulo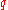 
. This conjecture is still open.
Lower bounds for sums of characters in polynomials
Karatsuba constructed an infinite sequence of primes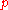
and a sequence of polynomials 
of degree 
with integer coefficients, such that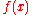 
is not a full square modulo 
,
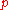and such that
In other words, for any
the value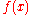 
turns out to be a quadratic residues modulo 
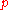. This result shows that André WeilAndré WeilAndré Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
's estimate
cannot be essentially improved and the right hand side of the latter inequality cannot be replaced by say the value
, where 
is an absolute constant.
Sums of characters on additive sequences
Karatsuba found a new method, making it possible to obtain rather precise estimates of sums of values of non-principal Dirichlet characters on additive sequences, that is, on sequences consisting of numbers of the form , where the variables
and 
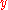runs through some sets
and 
independently of each other. The most characteristic example of that kind is the following claim which is applied in solving a wide class of problems, connected with summing up values of Dirichlet characters. Let 
be an arbitrarily small fixed number, 
, 
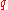a sufficiently large prime, 
a non-principal character modulo 
. Furthermore, let 
and 
be arbitrary subsets of the complete system of congruence classes modulo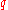 
, satisfying only the conditions 
, 
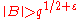. Then the following estimate holds:
-
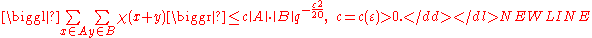
Karatsuba's method makes it possible to obtain non-trivial estimates of that sort in certain other cases when the conditions for the sets
and 
, formulated above, are replaced by different ones, for example: 
, 
In the case when
and 
are the sets of primes in intervals 
, 
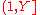respectively, where 
, 
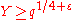, an estimate of the form
holds, where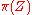
is the number of primes, not exceeding 
, 
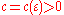, and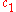 
is some absolute constant.
Distribution of power congruence classes and primitive roots in sparse sequences
Karatsuba obtained (2000) non-trivial estimates of sums of values of Dirichlet characters "with weights", that is, sums of components of the form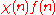
, where 
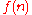is a function of natural argument. Estimates of that sort are applied in solving a wide class of problems of number theory, connected with distribution of power congruence classes, also primitive roots in certain sequences.
Let
be an integer, 
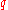a sufficiently large prime, 
, 
, 
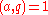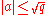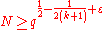, where 
, and set, finally,
(for an asymptotic expression for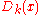
, see above, in the section on the multi-dimensional problem of Dirichlet divisors). For the sums 
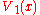and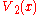 
of the values 
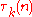, extended on the values 
, for which the numbers 
are quadratic residues (respectively, non-residues) modulo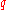 
, Karatsuba obtained asymptotic formulas of the form
-
.
Similarly, for the sum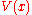
of values 
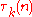, taken over all 
, for which 
is a primitive root modulo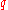 
, one gets an asymptotic expression of the form
-
,
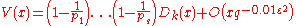where
are all prime divisors of the number 
.
Karatsuba applied his method also to the problems of distribution of power residues (non-residues) in the sequences of shifted primes
, of the integers of the type 
and some others.
Works of his later years
In his later years, apart from his research in number theory (see Karatsuba phenomenon), Karatsuba studied certain problems of theoretical physicsTheoretical physicsTheoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, in particular in the area of quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. Applying his ATS theoremATS theoremIn mathematics, the ATS theorem is the theorem on the approximation of atrigonometric sum by a shorter one. The application of the ATS theorem in certain problems of mathematical and theoretical physics can be very helpful....
and some other number-theoretic approaches, he obtained new results in the Jaynes–Cummings model in quantum opticsQuantum opticsQuantum optics is a field of research in physics, dealing with the application of quantum mechanics to phenomena involving light and its interactions with matter.- History of quantum optics :...
.
Personal life
He was married to Diana Vasil'evna Senchenko, a former student of the same year at MSU Faculty of Mechanics and Mathematics
Lomonosov Moscow State University, now Associate Professor at the Division of Mathematical methods in Economics at MSU Faculty of EconomicsMSU Faculty of EconomicsMSU Faculty of Economics is a faculty of the Moscow State University. It is one of the main educational centres in Russian Federation, preparing qualified economists with broad university education....
, Ph.D. in Mathematics. Their daughter, Ekaterina Anatol'evna Karatsuba, is now a leading research fellow (full Professor) at Dorodnitsyn Computing Centre, Ph.D. in Physics and Mathematics, D.Sci. in Physics and Mathematics.
All his life Karatsuba enjoyed many sports: in his younger years, athletics, weightlifting and wrestling, then hiking, rock climbing, caving and mountaineering. Eleven times, he climbed to a height over 7000 meters, conquering the mountains- Ismoil Somoni Peak (the highest in the USSR) in 1977 and
1985;- Lenin PeakLenin PeakLenin Peak , rises to in Gorno-Badakhshan on the border of Tajikistan and Kyrgyzstan, and is the second-highest point of both countries. It is considered one of the easiest 7,000 m peaks in the world to climb and it has by far the most ascents of any 7,000 m or higher peak on earth, with every...
in 1968 and 1979; - Peak KorzhenevskayaPeak KorzhenevskayaPeak Korzhenevskaya is the third highest peak in the Pamir Mountains of Tajikistan. It is one of the five "Snow Leopard Peaks" in the territory of theformer Soviet Union. It is named after Evgenia Korzhenevskaya, the wife of Russiangeographer Nikolai L...
in 1980, 1982, 1983, 1985, 1986, 1988 and
1991.
Four times he climbed Mount ElbrusMount ElbrusMount Elbrus is an inactive volcano located in the western Caucasus mountain range, in Kabardino-Balkaria and Karachay-Cherkessia, Russia, near the border of Georgia. Mt. Elbrus's peak is the highest in the Caucasus, in Russia...
. He hiked in the mountains of CaucasusCaucasusThe Caucasus, also Caucas or Caucasia , is a geopolitical region at the border of Europe and Asia, and situated between the Black and the Caspian sea...
, Pamir MountainsPamir MountainsThe Pamir Mountains are a mountain range in Central Asia formed by the junction or knot of the Himalayas, Tian Shan, Karakoram, Kunlun, and Hindu Kush ranges. They are among the world’s highest mountains and since Victorian times they have been known as the "Roof of the World" a probable...
and, especially in the last years of his life, Tian ShanTian ShanThe Tian Shan , also spelled Tien Shan, is a large mountain system located in Central Asia. The highest peak in the Tian Shan is Victory Peak , ....
in Zailiysky AlatauTrans-Ili AlatauTrans-Ili Alatau , , also spelt as Zailiyski Alatau, Zailiysk Alatau, etc., is a part of the Northern Tian Shan mountain system in Kazakhstan and Kyrgyzstan. It is the northernmost mountain range of Tian Shan stretching for about 350 km with maximal elevation of 4,973m . The term "Alatau" refers...
and Teskey Ala-TooTeskey Ala-Too RangeThe Teskey Ala-Too or Terskey Ala-Too is a mountain range in Kyrgyzstan's Tien-Shan that borders Issyk Kul and Kochkor Valley from the south. The length of the range is 354 km and highest peak -Yeltsin Peak...
.
He loved classical music and knew it very well, especially Johann Sebastian BachJohann Sebastian BachJohann Sebastian Bach was a German composer, organist, harpsichordist, violist, and violinist whose sacred and secular works for choir, orchestra, and solo instruments drew together the strands of the Baroque period and brought it to its ultimate maturity...
and Antonio VivaldiAntonio VivaldiAntonio Lucio Vivaldi , nicknamed because of his red hair, was an Italian Baroque composer, priest, and virtuoso violinist, born in Venice. Vivaldi is recognized as one of the greatest Baroque composers, and his influence during his lifetime was widespread over Europe...
. He regularly attended concerts in Moscow ConservatoryMoscow ConservatoryThe Moscow Conservatory is a higher musical education institution in Moscow, and the second oldest conservatory in Russia after St. Petersburg Conservatory. Along with the St...
, loved the concerts of Sviatoslav RichterSviatoslav RichterSviatoslav Teofilovich Richter was a Soviet pianist well known for the depth of his interpretations, virtuoso technique, and vast repertoire. He is widely considered one of the greatest pianists of the 20th century.-Childhood:...
, Leonid Kogan, Mstislav RostropovichMstislav RostropovichMstislav Leopoldovich Rostropovich, KBE , known to close friends as Slava, was a Soviet and Russian cellist and conductor. He was married to the soprano Galina Vishnevskaya. He is widely considered to have been the greatest cellist of the second half of the 20th century, and one of the greatest of...
, Viktor TretiakovViktor TretiakovViktor Tretiakov is a Russian violinist and conductor. Other spellings of his name are Victor, Tretyakov and Tretjakov.-Biography:...
, Andrei Korsakov and his
group "Concertino", Vladimir Ovchinnikov, Nikolai LuganskyNikolai LuganskyNikolai Lugansky is a Russian pianist from Moscow. At the age of five, before he had even started to learn the piano, he astonished his parents when he sat down at the piano and played a Beethoven sonata by ear, which he had just heard a relative play. He studied piano at the Moscow Central Music...
.
See also
- ATS theoremATS theoremIn mathematics, the ATS theorem is the theorem on the approximation of atrigonometric sum by a shorter one. The application of the ATS theorem in certain problems of mathematical and theoretical physics can be very helpful....
- Karatsuba algorithm
- The Karatsuba phenomenon
- Moore machineMoore machineIn the theory of computation, a Moore machine is a finite-state machine, whose output values are determined solely by its current state.-Name:The Moore machine is named after Edward F...
External links
- List of Research Works at Steklov Institute of MathematicsSteklov Institute of MathematicsSteklov Institute of Mathematics or Steklov Mathematical Institute is a research institute based in Moscow, specialized in mathematics, and a part of the Russian Academy of Sciences. It was established April 24, 1934 by the decision of the General Assembly of the Academy of Sciences of the USSR in...
-
- finding a lower bound for the number of solutions of inequalities of the form :
- Let
-
-
