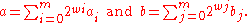Multiplication algorithm
Encyclopedia
A multiplication algorithm is an algorithm
(or method) to multiply
two numbers. Depending on the size of the numbers, different algorithms are in use. Efficient multiplication algorithms have existed since the advent of the decimal system.
level. It has been a standard part of the national primary-school mathematics curriculum in England and Wales since the late 1990s.
Both factors are broken up ("partitioned") into their hundreds, tens and units parts, and the products of the parts are then calculated explicitly in a relatively simple multiplication-only stage, before these contributions are then totalled to give the final answer in a separate addition stage.
Thus for example the calculation 34 × 13 could be computed using the grid
followed by addition to obtain 442, either in a single sum (see right), or through forming the row-by-row totals (300 + 40) + (90 + 12) = 340 + 102 = 442.
This calculation approach (though not necessarily with the explicit grid arrangement) is also known as the partial products algorithm. Its essence is the calculation of the simple multiplications separately, with all addition being left to the final gathering-up stage.
The grid method can in principle be applied to factors of any size, although the number of sub-products becomes cumbersome as the number of digits increases. Nevertheless it is seen as a usefully explicit method to introduce the idea of multiple-digit multiplications; and, in an age when most multiplication calculations are done using a calculator or a spreadsheet, it may in practice be the only multiplication algorithm that some students will ever need.
is used, a natural way of multiplying numbers is taught in schools
as long multiplication, sometimes called grade-school multiplication:
multiply the multiplicand by each digit of the multiplier and then add up all the properly shifted results. It requires memorization of the multiplication table
for single digits.
This is the usual algorithm for multiplying larger numbers by hand in base 10. Computers normally use a very similar shift and add algorithm in base 2. A person doing long multiplication on paper will write down all the products and then add them together; an abacus
-user will sum the products as soon as each one is computed.
23958233
5830 ×
------------
00000000 ( = 23,958,233 × 0)
71874699 ( = 23,958,233 × 30)
191665864 ( = 23,958,233 × 800)
119791165 ( = 23,958,233 × 5,000)
------------
139676498390 ( = 139,676,498,390 )
algorithm; that is, an algorithm that only needs working space proportional to the logarithm of the number of digits in the input (Θ(log n)). This is the double logarithm of the numbers being multiplied themselves (log log N). We don't include the input or output bits in this measurement, since that would trivially make the space requirement linear; instead we make the input bits read-only and the output bits write-only. (This just means that input and output bits are not counted as we count only read- AND writable bits.)
The method is simple: we add the columns right-to-left, keeping track of the carry as we go. We don't have to store the columns to do this. To show this, let the ith bit from the right of the first and second operands be denoted ai and bi respectively, both starting at i = 0, and let ri be the ith bit from the right of the result. Then

where c is the carry from the previous column. Provided neither c nor the total sum exceed log space, we can implement this formula in log space, since the indexes j and k each have O(log n) bits.
A simple inductive argument shows that the carry can never exceed n and the total sum for ri can never exceed 2n: the carry into the first column is zero, and for all other columns, there are at most n bits in the column, and a carry of at most n coming in from the previous column (by the induction hypothesis). Their sum is at most 2n, and the carry to the next column is at most half of this, or n. Thus both these values can be stored in O(log n) bits.
In pseudocode, the log-space algorithm is:
multiply(a[0..n−1], b[0..n−1]) // Arrays representing the binary representations
x ← 0
for i from 0 to 2n−1
for j from max(0,i+1−n) to min(i,n−1)column multiplication
k ← i − j
x ← x + (a[j] × b[k])
result[i] ← x mod 2
x ← floor(x/2)
implement this algorithm for various integer and floating-point sizes in hardware
or in microcode
. In arbitrary-precision arithmetic
, it's common to use long multiplication with the base set to 2w, where w is the number of bits in a word, for multiplying relatively small numbers.
To multiply two numbers with n digits using this method, one needs about n2 operations. More formally: using a natural size metric of number of digits, the time complexity of multiplying two n-digit numbers using long multiplication is Θ
(n2).
When implemented in software, long multiplication algorithms have to deal with overflow during additions, which can be expensive. For this reason, a typical approach is to represent the number in a small base b such that, for example, 8b2 is a representable machine integer (for example Richard Brent used this approach in his Fortran package MP); we can then perform several additions before having to deal with overflow. When the number becomes too large, we add part of it to the result or carry and map the remaining part back to a number less than b; this process is called normalization.
Sunzi mulitplication algorithm was first introduced to Arab countries by Al Khwarizmi in his book about Indian arithmetics; later also appeared in 10-11th century Kushyar ibn Labban
's book Principle of Hindu Reckoning.

 Lattice, or sieve, multiplication is algorithmically equivalent to long multiplication. It requires the preparation of a lattice (a grid drawn on paper) which guides the calculation and separates all the multiplications from the addition
Lattice, or sieve, multiplication is algorithmically equivalent to long multiplication. It requires the preparation of a lattice (a grid drawn on paper) which guides the calculation and separates all the multiplications from the addition
s. It was introduced to Europe in 1202 in Fibonacci
's Liber Abaci
. Leonardo described the operation as mental, using his right and left hands to carry the intermediate calculations. Matrakçı Nasuh
presented 6 different variants of this method in this 16th century book, Umdet-ul Hisab. It was widely used in Enderun schools across the Ottoman Empire. Napier's bones
, or Napier's rods also used this method, as published by Napier in 1617, the year of his death.
As shown in the example, the multiplicand and multiplier are written above and to the right of a lattice, or a sieve. It is found in Muhammad ibn Musa al-Khwarizmi
's "Arithmetic", one of Leonardo's sources mentioned by Sigler, author of "Fibonacci's Liber Abaci", 2002.
This algorithm
is also known as Peasant multiplication, because it has been widely used among those who are unschooled and thus have not memorized the multiplication tables required by long multiplication. The algorithm was also in use in ancient Egypt.
On paper, write down in one column the numbers you get when you repeatedly halve the multiplier, ignoring the remainder; in a column beside it repeatedly double the multiplicand. Cross out each row in which the last digit of the first number is even, and add the remaining numbers in the second column to obtain the product.
The main advantages of this method are that it can be taught quickly, no memorization is required, and it can be performed using tokens such as poker chips if paper and pencil are not available. It does however take more steps than long multiplication so it can be unwieldy when large numbers are involved.
Decimal: Binary:
11 3 1011 11
5 6 101 110
212 10 1100
1 24 1 11000
--- -----
33 100001
Describing the steps explicitly:
The method works because multiplication is distributive
, so:
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
(or method) to multiply
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
two numbers. Depending on the size of the numbers, different algorithms are in use. Efficient multiplication algorithms have existed since the advent of the decimal system.
Grid method
The grid method (or box method) is an introductory method for multiple-digit multiplication that is often taught to pupils at primary school or elementary schoolElementary school
An elementary school or primary school is an institution where children receive the first stage of compulsory education known as elementary or primary education. Elementary school is the preferred term in some countries, particularly those in North America, where the terms grade school and grammar...
level. It has been a standard part of the national primary-school mathematics curriculum in England and Wales since the late 1990s.
Both factors are broken up ("partitioned") into their hundreds, tens and units parts, and the products of the parts are then calculated explicitly in a relatively simple multiplication-only stage, before these contributions are then totalled to give the final answer in a separate addition stage.
Thus for example the calculation 34 × 13 could be computed using the grid
| 30 | 4 | |
|---|---|---|
| 10 | 300 | 40 |
| 3 | 90 | 12 |
followed by addition to obtain 442, either in a single sum (see right), or through forming the row-by-row totals (300 + 40) + (90 + 12) = 340 + 102 = 442.
This calculation approach (though not necessarily with the explicit grid arrangement) is also known as the partial products algorithm. Its essence is the calculation of the simple multiplications separately, with all addition being left to the final gathering-up stage.
The grid method can in principle be applied to factors of any size, although the number of sub-products becomes cumbersome as the number of digits increases. Nevertheless it is seen as a usefully explicit method to introduce the idea of multiple-digit multiplications; and, in an age when most multiplication calculations are done using a calculator or a spreadsheet, it may in practice be the only multiplication algorithm that some students will ever need.
Long multiplication
If a positional numeral systemNumeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
is used, a natural way of multiplying numbers is taught in schools
as long multiplication, sometimes called grade-school multiplication:
multiply the multiplicand by each digit of the multiplier and then add up all the properly shifted results. It requires memorization of the multiplication table
Multiplication table
In mathematics, a multiplication table is a mathematical table used to define a multiplication operation for an algebraic system....
for single digits.
This is the usual algorithm for multiplying larger numbers by hand in base 10. Computers normally use a very similar shift and add algorithm in base 2. A person doing long multiplication on paper will write down all the products and then add them together; an abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
-user will sum the products as soon as each one is computed.
Example
This example uses long multiplication to multiply 23,958,233 (multiplicand) by 5,830 (multiplier) and arrives at 139,676,498,390 for the result (product).23958233
5830 ×
------------
00000000 ( = 23,958,233 × 0)
71874699 ( = 23,958,233 × 30)
191665864 ( = 23,958,233 × 800)
119791165 ( = 23,958,233 × 5,000)
------------
139676498390 ( = 139,676,498,390 )
Space complexity
Let n be the total number of bits in the two input numbers. Long multiplication has the advantage that it can easily be formulated as a log spaceFL (complexity)
In computational complexity theory, the complexity class FL is the set of function problems which can be solved by a deterministic Turing machine in a logarithmic amount of memory space...
algorithm; that is, an algorithm that only needs working space proportional to the logarithm of the number of digits in the input (Θ(log n)). This is the double logarithm of the numbers being multiplied themselves (log log N). We don't include the input or output bits in this measurement, since that would trivially make the space requirement linear; instead we make the input bits read-only and the output bits write-only. (This just means that input and output bits are not counted as we count only read- AND writable bits.)
The method is simple: we add the columns right-to-left, keeping track of the carry as we go. We don't have to store the columns to do this. To show this, let the ith bit from the right of the first and second operands be denoted ai and bi respectively, both starting at i = 0, and let ri be the ith bit from the right of the result. Then

where c is the carry from the previous column. Provided neither c nor the total sum exceed log space, we can implement this formula in log space, since the indexes j and k each have O(log n) bits.
A simple inductive argument shows that the carry can never exceed n and the total sum for ri can never exceed 2n: the carry into the first column is zero, and for all other columns, there are at most n bits in the column, and a carry of at most n coming in from the previous column (by the induction hypothesis). Their sum is at most 2n, and the carry to the next column is at most half of this, or n. Thus both these values can be stored in O(log n) bits.
In pseudocode, the log-space algorithm is:
multiply(a[0..n−1], b[0..n−1]) // Arrays representing the binary representations
x ← 0
for i from 0 to 2n−1
for j from max(0,i+1−n) to min(i,n−1)column multiplication
k ← i − j
x ← x + (a[j] × b[k])
result[i] ← x mod 2
x ← floor(x/2)
Electronic usage
Some chipsIntegrated circuit
An integrated circuit or monolithic integrated circuit is an electronic circuit manufactured by the patterned diffusion of trace elements into the surface of a thin substrate of semiconductor material...
implement this algorithm for various integer and floating-point sizes in hardware
Hardware
Hardware is a general term for equipment such as keys, locks, hinges, latches, handles, wire, chains, plumbing supplies, tools, utensils, cutlery and machine parts. Household hardware is typically sold in hardware stores....
or in microcode
Microcode
Microcode is a layer of hardware-level instructions and/or data structures involved in the implementation of higher level machine code instructions in many computers and other processors; it resides in special high-speed memory and translates machine instructions into sequences of detailed...
. In arbitrary-precision arithmetic
Arbitrary-precision arithmetic
In computer science, arbitrary-precision arithmetic indicates that calculations are performed on numbers whose digits of precision are limited only by the available memory of the host system. This contrasts with the faster fixed-precision arithmetic found in most ALU hardware, which typically...
, it's common to use long multiplication with the base set to 2w, where w is the number of bits in a word, for multiplying relatively small numbers.
To multiply two numbers with n digits using this method, one needs about n2 operations. More formally: using a natural size metric of number of digits, the time complexity of multiplying two n-digit numbers using long multiplication is Θ
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n2).
When implemented in software, long multiplication algorithms have to deal with overflow during additions, which can be expensive. For this reason, a typical approach is to represent the number in a small base b such that, for example, 8b2 is a representable machine integer (for example Richard Brent used this approach in his Fortran package MP); we can then perform several additions before having to deal with overflow. When the number becomes too large, we add part of it to the result or carry and map the remaining part back to a number less than b; this process is called normalization.
Sunzi multiplication algorithm
Sunzi Mathematical Classic of 400AD detailed step by step multiplication algorithm with Rod calculusRod calculus
Rod calculus or rod calculation is the method of mathematical computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were replaced by the more convenient and faster abacus.-Hardware:...
Sunzi mulitplication algorithm was first introduced to Arab countries by Al Khwarizmi in his book about Indian arithmetics; later also appeared in 10-11th century Kushyar ibn Labban
Kushyar ibn Labban
Abul-Hasan Kūshyār ibn Labbān ibn Bashahri Gilani , also known as Kūshyār Gīlānī , was a Persian mathematician, geographer, and astronomer from Gilan, south of the Caspian Sea, Iran....
's book Principle of Hindu Reckoning.
Lattice multiplication


Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
s. It was introduced to Europe in 1202 in Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
's Liber Abaci
Liber Abaci
Liber Abaci is a historic book on arithmetic by Leonardo of Pisa, known later by his nickname Fibonacci...
. Leonardo described the operation as mental, using his right and left hands to carry the intermediate calculations. Matrakçı Nasuh
Matrakçi Nasuh
Nasuh bin Karagöz bin Abdullah el-Bosnavî , commonly known as Matrakçı Nasuh for his competence in the game called Matrak was a 16th century Ottoman mathematician, teacher, historian, geographer, cartographer, swordmaster, and miniaturist of...
presented 6 different variants of this method in this 16th century book, Umdet-ul Hisab. It was widely used in Enderun schools across the Ottoman Empire. Napier's bones
Napier's bones
Napier's bones is an abacus created by John Napier for calculation of products and quotients of numbers that was based on Arab mathematics and lattice multiplication used by Matrakci Nasuh in the Umdet-ul Hisab and Fibonacci writing in the Liber Abaci. Also called Rabdology...
, or Napier's rods also used this method, as published by Napier in 1617, the year of his death.
As shown in the example, the multiplicand and multiplier are written above and to the right of a lattice, or a sieve. It is found in Muhammad ibn Musa al-Khwarizmi
Muhammad ibn Musa al-Khwarizmi
'There is some confusion in the literature on whether al-Khwārizmī's full name is ' or '. Ibn Khaldun notes in his encyclopedic work: "The first who wrote upon this branch was Abu ʿAbdallah al-Khowarizmi, after whom came Abu Kamil Shojaʿ ibn Aslam." . 'There is some confusion in the literature on...
's "Arithmetic", one of Leonardo's sources mentioned by Sigler, author of "Fibonacci's Liber Abaci", 2002.
- During the multiplication phase, the lattice is filled in with two-digit products of the corresponding digits labeling each row and column: the tens digit goes in the top-left corner.
- During the addition phase, the lattice is summed on the diagonals.
- Finally, if a carry phase is necessary, the answer as shown along the left and bottom sides of the lattice is converted to normal form by carrying ten's digits as in long addition or multiplication.
Example
The pictures on the right show how to calculate 345 × 12 using lattice multiplication. As a more complicated example, consider the picture below displaying the computation of 23,958,233 multiplied by 5,830 (multiplier); the result is 139,676,498,390. Notice 23,958,233 is along the top of the lattice and 5,830 is along the right side. The products fill the lattice and the sum of those products (on the diagonal) are along the left and bottom sides. Then those sums are totaled as shown.
|
|
= 139,676,498,390 |
Peasant or binary multiplication
In base 2, long multiplication reduces to a nearly trivial operation. For each '1' bit in the multiplier, shift the multiplicand an appropriate amount and then sum the shifted values. Depending on computer processor architecture and choice of multiplier, it may be faster to code this algorithm using hardware bit shifts and adds rather than depend on multiplication instructions, when the multiplier is fixed and the number of adds required is small.This algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
is also known as Peasant multiplication, because it has been widely used among those who are unschooled and thus have not memorized the multiplication tables required by long multiplication. The algorithm was also in use in ancient Egypt.
On paper, write down in one column the numbers you get when you repeatedly halve the multiplier, ignoring the remainder; in a column beside it repeatedly double the multiplicand. Cross out each row in which the last digit of the first number is even, and add the remaining numbers in the second column to obtain the product.
The main advantages of this method are that it can be taught quickly, no memorization is required, and it can be performed using tokens such as poker chips if paper and pencil are not available. It does however take more steps than long multiplication so it can be unwieldy when large numbers are involved.
Examples
This example uses peasant multiplication to multiply 11 by 3 to arrive at a result of 33.Decimal: Binary:
11 3 1011 11
5 6 101 110
2
1 24 1 11000
--- -----
33 100001
Describing the steps explicitly:
- 11 and 3 are written at the top
- 11 is halved (5.5) and 3 is doubled (6). The fractional portion is discarded (5.5 becomes 5).
- 5 is halved (2.5) and 6 is doubled (12). The fractional portion is discarded (2.5 becomes 2). The figure in the left column (2) is even, so the figure in the right column (12) is discarded.
- 2 is halved (1) and 12 is doubled (24).
- All not-scratched-out values are summed: 3 + 6 + 24 = 33.
The method works because multiplication is distributive
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
, so:
-

A more complicated example, using the figures from the earlier examples (23,958,233 and 5,830):
Decimal: Binary:
58302395823310110110001101011011011001001011011001
2915 47916466 101101100011 10110110110010010110110010
1457 95832932 10110110001 101101101100100101101100100
72819166586410110110001011011011001001011011001000
36438333172810110110010110110110010010110110010000
18276666345610110110101101101100100101101100100000
91 1533326912 1011011 1011011011001001011011001000000
45 3066653824 101101 10110110110010010110110010000000
22613330764810110101101101100100101101100100000000
11 12266615296 1011 1011011011001001011011001000000000
5 24533230592 101 10110110110010010110110010000000000
24906646118410101101101100100101101100100000000000
1 98132922368 1 1011011011001001011011001000000000000
------------ 1022143253354344244353353243222210110 (before carry)
139676498390 10000010000101010111100011100111010110
Shift and add
Most computers use a "shift and add" algorithm for multiplying small integers. Both base 2 long multiplication and base 2 peasant multiplication reduce to this same algorithm.
In base 2, multiplying by the single digit of the multiplier reduces to a simple series of logical AND operations. Each partial product is added to a running sum as soon as each partial product is computed. Most currently available microprocessors implement this or other similar algorithms (such as Booth encoding) for various integer and floating-point sizes in hardware multipliers or in microcodeMicrocodeMicrocode is a layer of hardware-level instructions and/or data structures involved in the implementation of higher level machine code instructions in many computers and other processors; it resides in special high-speed memory and translates machine instructions into sequences of detailed...
.
On currently available processors, a bit-wise shift instruction is faster than a multiply instruction and can be used to multiply (shift left) and divide (shift right) by powers of two. Multiplication by a constant and division by a constant can be implemented using a sequence of shifts and adds or subtracts. For example, there are several ways to multiply by 10 using only bit-shift and addition.
((x << 2) + x) << 1 # Here x*10 => x*[(2^2+1)*2]
(x << 3) + (x << 1) # Here x*10 => x*[(2^3+2)]
In some cases such sequences of shifts and adds or subtracts will outperform hardware multipliers and especially dividers. A division by a number of the form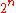 or
or  often can be converted to such a short sequence.
often can be converted to such a short sequence.
These types of sequences have to always be used for computers that do not have a "multiply" instruction, and can also be used by extension to floating point numbers if one replaces the shifts with computation of 2*x as x+x, as these are logically equivalent.
Quarter square multiplication
Two quantities can be multiplied using quarter squares by employing the following identity attributed to Babylonian mathematicsBabylonian mathematicsBabylonian mathematics refers to any mathematics of the people of Mesopotamia, from the days of the early Sumerians to the fall of Babylon in 539 BC. Babylonian mathematical texts are plentiful and well edited...
(2000–1600 BC)
-

If is odd then will also be odd, this means any fraction will cancel out so no accuracy is lost by discarding the remainders. Below is a lookup table of quarter squares with the remainder discarded for the digits 0 through 18,, this allows for the multiplication of numbers up to .
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 0 1 2 4 6 9 12 16 20 25 30 36 42 49 56 64 72 81
If, for example, you wanted to multiply 9 by 3, you observe that the sum and difference are 12 and 6 respectively. Looking both those values up on the table yields 36 and 9, the difference of which is 27, which is the product of 9 and 3.
Antoine Voisin published a table of quarter squares from 1 to 1000 in 1817 as an aid in multiplication. A larger table of quarter squares from 1 to 100000 was published by Samuel Laundy in 1856, and a table from 1 to 200000 by Joseph Blater in 1888.
Quarter square multipliers were used in analog computerAnalog computerAn analog computer is a form of computer that uses the continuously-changeable aspects of physical phenomena such as electrical, mechanical, or hydraulic quantities to model the problem being solved...
s to form an analog signalAnalog signalAn analog or analogue signal is any continuous signal for which the time varying feature of the signal is a representation of some other time varying quantity, i.e., analogous to another time varying signal. It differs from a digital signal in terms of small fluctuations in the signal which are...
that was the product of two analog input signals. In this application, the sum and difference of two input voltageVoltageVoltage, otherwise known as electrical potential difference or electric tension is the difference in electric potential between two points — or the difference in electric potential energy per unit charge between two points...
s are formed using operational amplifierOperational amplifierAn operational amplifier is a DC-coupled high-gain electronic voltage amplifier with a differential input and, usually, a single-ended output...
s. The square of each of these is approximated using piecewise linear circuits. Finally the difference of the two squares is formed and scaled by a factor of one fourth using yet another operational amplifier.
In 1980, Everett L. Johnson proposed using the quarter square method in a digitalDigitalA digital system is a data technology that uses discrete values. By contrast, non-digital systems use a continuous range of values to represent information...
multiplier. To form the product of two 8-bit integers, for example, the digital device forms the sum and difference, looks both quantities up in a table of squares, takes the difference of the results, and divides by four by shifting two bits to the right. For 8-bit integers the table of quarter squares will have 29 entries of 16 bits each.
The Quarter square multiplier technique has also benefitted 8 bit systems that do not have any support for a hardware multiplier. Steven Judd implemented this for the 6502.
Fast multiplication algorithms for large inputs
Gauss's complex multiplication algorithm
Complex multiplication normally involves four multiplications. By 1805 GaussGaussGauss may refer to:*Carl Friedrich Gauss, German mathematician and physicist*Gauss , a unit of magnetic flux density or magnetic induction*GAUSS , a software package*Gauss , a crater on the moon...
had discovered a way of reducing the number of multiplications to three.
The product (a + bi) · (c + di) can be calculated in the following way.
- k1 = c · (a + b)
- k2 = a · (d − c)
- k3 = b · (c + d)
- Real part = k1 − k3
- Imaginary part = k1 + k2.
This algorithm uses only three multiplications, rather than four, and five additions or subtractions rather than two. If a multiply is more expensive than three adds or subtracts, as when calculating by hand, then there is a gain in speed. On modern computers a multiply and an add can take about the same time so there may be no speed gain. There is a trade-off in that there may be some loss of precision when using floating point.
For fast Fourier transformFast Fourier transformA fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
s the complex multiplies involve constant 'twiddle' factors and two of the adds can be precomputed. Only three multiplies and three adds are required, and modern hardware can often overlap multiplies and adds.
Karatsuba multiplication
For systems that need to multiply numbers in the range of several thousand digits, such as computer algebra systemComputer algebra systemA computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
s and bignum libraries, long multiplication is too slow. These systems may employ Karatsuba multiplication, which was discovered in 1960 (published in 1962). The heart of Karatsuba's method lies in the observation that two-digit multiplication can be done with only three rather than the four multiplications classically required. Suppose we want to multiply two 2-digit numbers: x1x2· y1y2:
- compute x1 · y1, call the result A
- compute x2 · y2, call the result B
- compute (x1 + x2) · (y1 + y2), call the result C
- compute C − A − B, call the result K; this number is equal to x1 · y2 + x2 · y1
- compute A · 100 + K · 10 + B.
Bigger numbers x1x2 can be split into two parts x1 and x2. Then the method works analogously. To compute these three products of m-digit numbers, we can employ the same trick again, effectively using recursionRecursionRecursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
. Once the numbers are computed, we need to add them together (step 5.), which takes about n operations.
Karatsuba multiplication has a time complexity of OBig O notationIn mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(nlog23). The number log23 is approximately 1.585, so this method is significantly faster than long multiplication. Because of the overhead of recursion, Karatsuba's multiplication is slower than long multiplication for small values of n; typical implementations therefore switch to long multiplication if n is below some threshold.
Later the Karatsuba method was called ‘divide and conquerDivide and conquer algorithmIn computer science, divide and conquer is an important algorithm design paradigm based on multi-branched recursion. A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same type, until these become simple enough to be solved directly...
’, the other names of this method, used at the present, are ‘binary splittingBinary splittingIn mathematics, binary splitting is a technique for speeding up numerical evaluation of many types of series with rational terms. In particular, it can be used to evaluate hypergeometric series at rational points...
’ and ‘dichotomy principle’.
The appearance of the method ‘divide and conquer’ was the starting point of the theory of fast multiplications. A number of authors (among them Toom, Cook and Schönhage) continued to look for an algorithm of multiplication with the complexity close to the optimal one, and 1971 saw the construction of the Schönhage–Strassen algorithm, which maintained the best known (until 2007) upper bound for M(n).
The Karatsuba ‘divide and conquer’ is the most fundamental and general fast method. Hundreds of different algorithms are constructed on its basis. Among these algorithms the most well known are the algorithms based on Fast Fourier TransformFast Fourier transformA fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT) and Fast Matrix Multiplication.
Toom–Cook
Another method of multiplication is called Toom–Cook or Toom-3. The Toom–Cook method splits each number to be multiplied into multiple parts. The Toom–Cook method is one of the generalizations of the Karatsuba method. A three-way Toom–Cook can do a size-N3 multiplication for the cost of five size-N multiplications, improvement by a factor of 9/5 compared to the Karatsuba method's improvement by a factor of 4/3.
Although using more and more parts can reduce the time spent on recursive multiplications further, the overhead from additions and digit management also grows. For this reason, the method of Fourier transforms is typically faster for numbers with several thousand digits, and asymptotically faster for even larger numbers.
Fourier transform methods
The idea, due to StrassenVolker StrassenVolker Strassen is a German mathematician, a professor emeritus in the department of mathematics and statistics at the University of Konstanz.-Biography:Strassen was born on April 29, 1936, in Düsseldorf-Gerresheim....
(1968), is the following: We choose the largest integer w that will not cause overflowInteger overflowIn computer programming, an integer overflow occurs when an arithmetic operation attempts to create a numeric value that is too large to be represented within the available storage space. For instance, adding 1 to the largest value that can be represented constitutes an integer overflow...
during the process outlined below. Then we split the two numbers into m groups of w bits
We can then say that
by setting bj = 0 and ai = 0 for j, i > m, k = i + j and {ck} as the convolutionConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of {ai} and {bj}. Using the convolution theoremConvolution theoremIn mathematics, the convolution theorem states that under suitableconditions the Fourier transform of a convolution is the pointwise product of Fourier transforms. In other words, convolution in one domain equals point-wise multiplication in the other domain...
ab can be computed by- Computing the fast Fourier transformFast Fourier transformA fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
s of {ai} and {bj}, - Multiplying the two results entry by entry,
- Computing the inverse Fourier transform and
- Adding the part of ck that is greater than 2w to ck+1.
The Schönhage–Strassen algorithm, described in 1971 by SchönhageArnold SchönhageArnold Schönhage is a mathematician and computer scientist and Professor Emeritus at Rheinische Friedrich-Wilhelms-Universität, Bonn. He was also professor in Tübingen and Konstanz...
and Strassen, has a time complexity of Θ(n log(n) log(log(n))) and is used in practice for numbers with more than 10,000 to 40,000 decimal digits. In 2007 this was improved by Martin Fürer (Fürer's algorithmFürer's algorithmFürer's algorithm is an integer multiplication algorithm for very large numbers possessing a very low asymptotic complexity. It was created in 2007 by Swiss mathematician Martin Fürer of Pennsylvania State University as an asymptotically faster algorithm than its predecessor, the...
) to give a time complexity of n log(n) 2Θ(log*(n)) using Fourier transforms over complex numbers. Anindya De, Chandan Saha, Piyush Kurur and Ramprasad Saptharishi gave a similar algorithm using modular arithmeticModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
in 2008 achieving the same running time. However, these latter algorithms are only faster than Schönhage–Strassen for impractically large inputs.
Using number-theoretic transforms instead of discrete Fourier transformDiscrete Fourier transformIn mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
s avoids rounding error problems by using modular arithmetic instead of floating-pointFloating pointIn computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
arithmetic.
FFT-based algorithms multiply polynomialsPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
, not numbers. But it is trivial to convert a number to the corresponding polynomial and then restore resulting number from the polynomial.
Linear time multiplication
Knuth describes computational models in which two n-bit numbers can be multiplied in linear time. The most realistic of these requires that any memory location can be accessed in constant time (the so-called RAM model). The approach is to use the FFT based method described above, packing log n bits into each coefficient of the polynomials and doing all computations with 6 log n bits of accuracy. The time complexity is now O( nM ) where M is the time needed to multiply two log n - bit numbers. By precomputing a linear size multiplication lookup table of all pairs of numbers of (log n)/2 bits, M is simply the time needed to perform a constant number of table lookups. If one assumes this takes constant time per table lookup as is true in the unit-cost word RAM model, then the overall algorithm is linear time.
Lower bounds
There is a trivial lower bound of Ω(n) for multiplying two n-bit numbers on a single processor; no matching algorithm (on conventional Turing machines) nor any better lower bound is known. Multiplication lies outside of AC0[p] for any prime p, meaning there is no family of constant-depth, polynomial (or even subexponential) size circuits using AND, OR, NOT, and MODp gates that can compute a product. This follows from a constant-depth reduction of MODq to multiplication. Lower bounds for multiplication are also known for some classes of branching programs.
Polynomial multiplication
All the above multiplication algorithms can also be expanded to multiply polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s. For instance the Strassen algorithm may be used for polynomial multiplication
See also
- Binary multiplierBinary multiplierA binary multiplier is an electronic circuit used in digital electronics, such as a computer, to multiply two binary numbers. It is built using binary adders....
- Division (digital)Division (digital)Several algorithms exist to perform division in digital designs. These algorithms fall into two main categories: slow division and fast division. Slow division algorithms produce one digit of the final quotient per iteration. Examples of slow division include restoring, non-performing restoring,...
- LogarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
- Mental calculationMental calculationMental calculation comprises arithmetical calculations using only the human brain, with no help from calculators, computers, or pen and paper. People use mental calculation when computing tools are not available, when it is faster than other means of calculation , or in a competition context...
- ProsthaphaeresisProsthaphaeresisProsthaphaeresis was an algorithm used in the late 16th century and early 17th century for approximate multiplication and division using formulas from trigonometry. For the 25 years preceding the invention of the logarithm in 1614, it was the only known generally-applicable way of approximating...
- Slide ruleSlide ruleThe slide rule, also known colloquially as a slipstick, is a mechanical analog computer. The slide rule is used primarily for multiplication and division, and also for functions such as roots, logarithms and trigonometry, but is not normally used for addition or subtraction.Slide rules come in a...
- Trachtenberg systemTrachtenberg systemThe Trachtenberg System is a system of rapid mental calculation. The system consists of a number of readily memorized operations that allow one to perform arithmetic computations very quickly. It was developed by the Jewish engineer Jakow Trachtenberg in order to keep his mind occupied while being...
- Horner schemeHorner schemeIn numerical analysis, the Horner scheme , named after William George Horner, is an algorithm for the efficient evaluation of polynomials in monomial form. Horner's method describes a manual process by which one may approximate the roots of a polynomial equation...
for evaluation of a polynomial
Basic arithmetic
- The Many Ways of Arithmetic in UCSMP Everyday Mathematics
- A Powerpoint presentation about ancient mathematics
- Lattice Multiplication Flash Video
Advanced algorithms
-