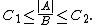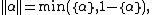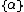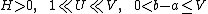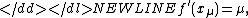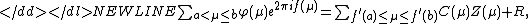ATS theorem
Encyclopedia
In mathematics, the ATS theorem is the theorem on the approximation of a
trigonometric sum by a shorter one. The application of the ATS theorem in certain problems of mathematical and theoretical physics can be very helpful.
and mathematical physics
, sums of the form
trigonometric sum by a shorter one. The application of the ATS theorem in certain problems of mathematical and theoretical physics can be very helpful.
History of the problem
In some fields of mathematicsMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, sums of the form
-
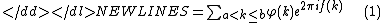
are under study.
Here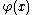 and
and 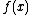 are real valued functions of a real
are real valued functions of a real
argument, and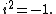
Such sums appear, for example, in number theoryNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
in the analysis of the
Riemann zeta function, in the solution of problems connected with
integer points in the domains on plane and in space, in the study of the
Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, and in the solution of such differential equations as the wave equationWave equationThe wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
, the potential equation, the heat conductivityHeat equationThe heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
equation.
The problem of approximation of the series (1) by a suitable function was studied already by EulerLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
and
PoissonSiméon Denis PoissonSiméon Denis Poisson , was a French mathematician, geometer, and physicist. He however, was the final leading opponent of the wave theory of light as a member of the elite l'Académie française, but was proven wrong by Augustin-Jean Fresnel.-Biography:...
.
We shall define
the length of the sum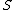
to be the number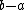
(for the integers and
and 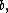 this is the number of the summands in
this is the number of the summands in 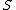 ).
).
Under certain conditions on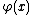 and
and 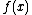
the sum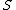 can be
can be
substituted with good accuracy by another sum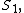
-

where the length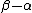 is far less than
is far less than 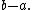
First relations of the form
-
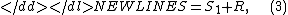
where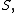
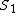 are the sums (1) and (2) respectively,
are the sums (1) and (2) respectively, 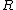 is
is
a remainder term, with concrete functions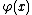 and
and 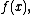
were obtained by G. H. HardyG. H. HardyGodfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
and J. E. Littlewood ,,
when they
deduced approximate functional equation for the Riemann zeta function
$\zeta(s)$ and by I. M. Vinogradov , in the study of
the amounts of integer points in the domains on plane.
In general form the theorem
was proved by J. Van der CorputJohannes van der CorputJohannes Gualtherus van der Corput was a Dutch mathematician, working in the field of analytic number theory....
, (on the recent
results connected with the Van der Corput theorem one can read at
).
In every one of the above-mentioned works,
some restrictions on the functions
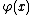 and
and 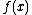 were imposed. With
were imposed. With
convenient (for applications) restrictions on
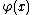 and
and 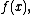 the theorem was proved by A. A. KaratsubaAnatolii Alexeevitch KaratsubaAnatolii Alexeevitch Karatsuba was a Russian mathematician, who authored the first fast multiplication method: the Karatsuba algorithm, a fast procedure for multiplying large numbers.- Studies and work :...
the theorem was proved by A. A. KaratsubaAnatolii Alexeevitch KaratsubaAnatolii Alexeevitch Karatsuba was a Russian mathematician, who authored the first fast multiplication method: the Karatsuba algorithm, a fast procedure for multiplying large numbers.- Studies and work :...
in (see also ,).
Certain notations
[1]. For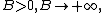
or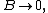 the record
the record
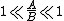
means that there are the constants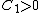
and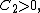
such that
[2]. For a real number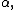 the record
the record
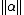 means that
means that
where
is the fractional part of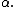
ATS theorem
Let the real functions ƒ(x) and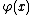 satisfy on the segment [a, b] the following conditions:
satisfy on the segment [a, b] the following conditions:
1)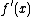 and
and 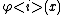 are continuous;
are continuous;
2) there exist numbers
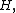
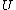 and
and 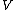 such that
such that
-
-
-
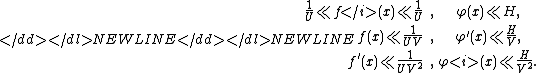
Then, if we define the numbers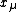 from the equation
from the equation
-
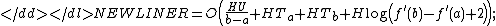
-
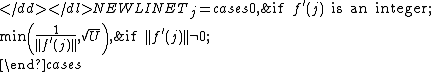
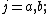
-
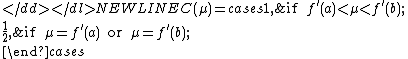
-
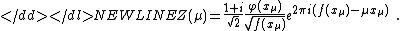
The most simple variant of the formulated theorem is the statement, which is called in the literature the Van der Corput lemma.
Van der Corput lemma
Let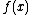 be a real differentiable function in the interval
be a real differentiable function in the interval
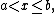 moreover, inside of this interval, its derivative
moreover, inside of this interval, its derivative
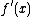 is a monotonic and a sign-preserving function, and for the constant
is a monotonic and a sign-preserving function, and for the constant 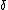 such that
such that 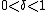 satisfies the inequality
satisfies the inequality
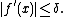 Then
Then
-
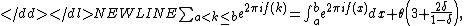
where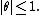
Remark
If the parameters and
and 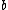 are integers, then it is possible to substitute the last relation by the following ones:
are integers, then it is possible to substitute the last relation by the following ones:
-
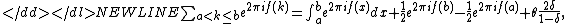
where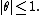
On the applications of ATS to the problems of physics see ,; see also ,.
-
-
-
-
-
-
-
-
-