
Selberg integral
Encyclopedia
In mathematics the Selberg integral is a generalization of Euler beta function to n dimensions introduced and proven by .
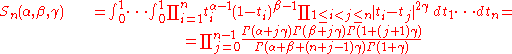
Selberg's formula implies Dixon's identity
for well poised hypergeometric series, and some special cases of Dyson's conjecture.
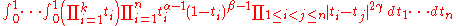
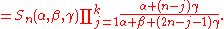
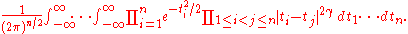
It is the partition function for a gas of point charges moving on a line that are attracted to the origin .
Its value can be deduced from that of the Selberg integral, and is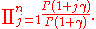
This was conjectured by , who were unaware of Selberg's earlier work.
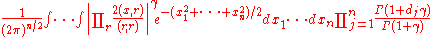
The product is over the roots r of the roots system and the numbers dj are the degrees of the generators of the ring of invariants of the reflection group.
gave a uniform proof for all crystallographic reflection groups. Several years later he proved it in full generality , making use of computer-aided calculations by Garvan.
Selberg's integral formula
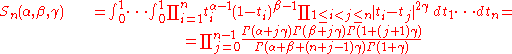
Selberg's formula implies Dixon's identity
Dixon's identity
In mathematics, Dixon's identity is any of several different but closely related identities proved by A. C. Dixon, some involving finite sums of products of three binomial coefficients, and some evaluating a hypergeometric sum...
for well poised hypergeometric series, and some special cases of Dyson's conjecture.
Aomoto's integral formula
proved a slightly more general integral formula: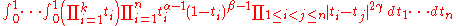
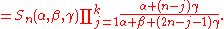
Mehta's integral
Mehta's integral is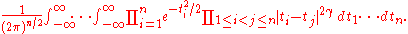
It is the partition function for a gas of point charges moving on a line that are attracted to the origin .
Its value can be deduced from that of the Selberg integral, and is
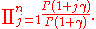
This was conjectured by , who were unaware of Selberg's earlier work.
Macdonald's integral
conjectured the following extension of Mehta's integral to all finite root systems, Mehta's original case corresponding to the An−1 root system.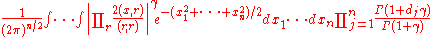
The product is over the roots r of the roots system and the numbers dj are the degrees of the generators of the ring of invariants of the reflection group.
gave a uniform proof for all crystallographic reflection groups. Several years later he proved it in full generality , making use of computer-aided calculations by Garvan.

