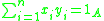Separable algebra
Encyclopedia
A separable algebra is a kind of semisimple algebra
. It is a generalization to associative algebra
s of the notion of a separable field extension
.
. An associative K-algebra A is said to be separable if for every field extension
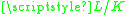the algebra 
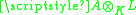is semisimple.
There is a classification theorem for separable algebras: separable algebras are the same as finite products of matrix algebras over division algebras whose centers are finite dimensional separable field extensions
of the field K. If K is a perfect field
--- for example a field of characteristic zero, or a finite field, or an algebraically closed field --- then every extension of K is separable. As a result, if K is a perfect field, separable algebras are the same as finite products of matrix algebras over division algebras whose centers are finite-dimensional field extensions of the field K. In other words, if K is a perfect field, there is no difference between a separable algebra over K and a finite-dimensional semisimple algebra
over K.
There are a several equivalent characterizations of separable algebras. First, an algebra A is separable if and only if there exists an element
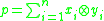
in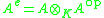
such that
and ap = pa for all a in A. Such an element p is called a separability idempotent, since it satisfies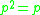
. A generalized theorem of Maschke shows these this characterization of separable algebras is equivalent to the definition given above.
Second, an algebra A is separable if and only if it is projective
when considered as a left module of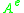
in the usual way.
Third, an algebra A is separable if and only if it is flat
when considered as a right module of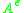
in the usual (but perhaps not quite standard) way. See Aguiar's note below for more details.
Furthermore, a result of Eilenberg and Nakayama that any separable algebra can be given the structure of a symmetric Frobenius algebra
. Since the underlying vector space of a Frobenius algebra is isomorphic to its dual, any Frobenius algebra is necessarily finite dimensional, and so the same is true for separable algebras.
A separable algebra is said to be strongly separable if there exists a separability idempotent that is symmetric, meaning
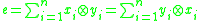
An algebra is strongly separable if and only if its trace form is nondegenerate, thus making the algebra into a special Frobenius algebra.
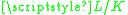is a field extension, then L is separable as an associative K-algebra if and only if the extension of field is separable
.
If L/K has primitive element a with irreducible polynomial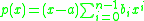
, then a separability idempotent is given by 
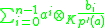. The tensorands are dual bases for the trace map: if 
are the distinct K-monomorphisms of L into an algebraic closure of K, the trace mapping Tr of L into K is defined by Tr(x) = 
. The trace map and its dual bases make explicit L as a Frobenius algebra
over K.
K[G] is a separable K-algebra.
A separability idempotent is given by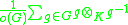
.
) restricts to an S-S-bimodule.
The ring extension R over S is said to be a separable extension if all short exact sequences of R-R-bimodules that are split as R-S-bimodules also split as R-R-bimodules. For example, the multiplication mapping m :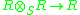
given by 
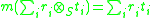is an R-R-bimodule epimorphism, which is split as an R-S-bimodule epi by the right inverse mapping 
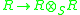given by
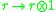. If R is a separable extension over S, then the multiplication mapping is split as an R-R-bimodule epi, so there is a right inverse s of m satisfying for s(1) := e, re = er for all r in R, and m(e) = 1. Conversely, if such an element (called a separability element in the tensor-square) exists, one shows by a judicious use of this element (like Maschke, applying its components within and without the splitting maps) that R is a separable extension of S.
Equivalently, the relative Hochschild cohomology groups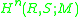
of (R,S) in any coefficient bimodule M is zero for n > 0. Examples of separable extensions are many including first separable algebras where R = separable algebra and S = 1 times the ground field. More interestingly, any ring R with elements a and b satisfying ab = 1, but ba different from 1, is a separable extension over the subring S generated by 1 and bRa.
An interesting theorem in the area is that of J. Cuadra that a separable Hopf-Galois extension R | S has finitely generated natural S-module R. A fundamental fact about a separable extension R | S is that it is left or right semisimple extension: a short exact sequence of left or right R-modules that is split as S-modules, is split as R-modules. In terms of G. Hochschild's relative homological algebra, one says that all R-modules are relative (R,S)-projective. Usually relative properties of subrings or ring extensions, such as the notion of separable extension, serve to promote theorems that say that the over-ring shares a property of the subring. For example, a separable extension R of a semisimple algebra S has R semisimple, which follows from the preceding discussion.
There is the celebrated Jans theorem that a finite group algebra A over a field of
characteristic p is of finite representation type if and only if its Sylow p-subgroup is cyclic: the clearest proof is to note this fact for p-groups, then note that the group algebra is a separable extension of its Sylow p-subgroup algebra B as the index is coprime to the characteristic. The separability condition above will imply every finitely generated A-module M is isomorphic to a direct summand
in its restricted, induced module. But if B has finite representation type, the restricted module
is uniquely a direct sum of multiples of finitely many indecomposables, which induce to a finite number of constituent indecomposable modules of which M is a direct sum. Hence A is of finite representation type if B is. The converse if proven by a similar argument noting that every subgroup algebra B is a B-bimodule direct summand of a group algebra A.
Semisimple algebra
In ring theory, a semisimple algebra is an associative algebra which has trivial Jacobson radical...
. It is a generalization to associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
s of the notion of a separable field extension
Separable extension
In modern algebra, an algebraic field extension E\supseteq F is a separable extension if and only if for every \alpha\in E, the minimal polynomial of \alpha over F is a separable polynomial . Otherwise, the extension is called inseparable...
.
Definition and First Properties
Let K be a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. An associative K-algebra A is said to be separable if for every field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
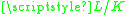the algebra 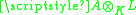is semisimple.There is a classification theorem for separable algebras: separable algebras are the same as finite products of matrix algebras over division algebras whose centers are finite dimensional separable field extensions
Separable extension
In modern algebra, an algebraic field extension E\supseteq F is a separable extension if and only if for every \alpha\in E, the minimal polynomial of \alpha over F is a separable polynomial . Otherwise, the extension is called inseparable...
of the field K. If K is a perfect field
Perfect field
In algebra, a field k is said to be perfect if any one of the following equivalent conditions holds:* Every irreducible polynomial over k has distinct roots.* Every polynomial over k is separable.* Every finite extension of k is separable...
--- for example a field of characteristic zero, or a finite field, or an algebraically closed field --- then every extension of K is separable. As a result, if K is a perfect field, separable algebras are the same as finite products of matrix algebras over division algebras whose centers are finite-dimensional field extensions of the field K. In other words, if K is a perfect field, there is no difference between a separable algebra over K and a finite-dimensional semisimple algebra
Semisimple algebra
In ring theory, a semisimple algebra is an associative algebra which has trivial Jacobson radical...
over K.
There are a several equivalent characterizations of separable algebras. First, an algebra A is separable if and only if there exists an element
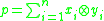
in
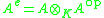such that
and ap = pa for all a in A. Such an element p is called a separability idempotent, since it satisfies
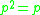. A generalized theorem of Maschke shows these this characterization of separable algebras is equivalent to the definition given above.Second, an algebra A is separable if and only if it is projective
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
when considered as a left module of
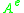in the usual way.Third, an algebra A is separable if and only if it is flat
Flat module
In Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
when considered as a right module of
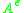in the usual (but perhaps not quite standard) way. See Aguiar's note below for more details.Furthermore, a result of Eilenberg and Nakayama that any separable algebra can be given the structure of a symmetric Frobenius algebra
Frobenius algebra
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in...
. Since the underlying vector space of a Frobenius algebra is isomorphic to its dual, any Frobenius algebra is necessarily finite dimensional, and so the same is true for separable algebras.
A separable algebra is said to be strongly separable if there exists a separability idempotent that is symmetric, meaning
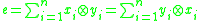
An algebra is strongly separable if and only if its trace form is nondegenerate, thus making the algebra into a special Frobenius algebra.
Commutative separable algebras
If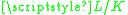 is a field extension, then L is separable as an associative K-algebra if and only if the extension of field is separableSeparable extension
In modern algebra, an algebraic field extension E\supseteq F is a separable extension if and only if for every \alpha\in E, the minimal polynomial of \alpha over F is a separable polynomial . Otherwise, the extension is called inseparable...
.
If L/K has primitive element a with irreducible polynomial
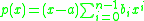, then a separability idempotent is given by 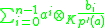. The tensorands are dual bases for the trace map: if are the distinct K-monomorphisms of L into an algebraic closure of K, the trace mapping Tr of L into K is defined by Tr(x) = . The trace map and its dual bases make explicit L as a Frobenius algebraFrobenius algebra
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in...
over K.
Examples
If K is a field and G is a finite group such that the order of G is invertible in K, then the group ringGroup ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
K[G] is a separable K-algebra.
A separability idempotent is given by
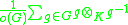.Separable Extensions for Noncommutative Rings
Let R be an associative ring with unit 1, and S a subring of R containing 1. Notice that an R-R-bimodule (see module theory and homological algebraHomological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
) restricts to an S-S-bimodule.
The ring extension R over S is said to be a separable extension if all short exact sequences of R-R-bimodules that are split as R-S-bimodules also split as R-R-bimodules. For example, the multiplication mapping m :
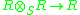given by 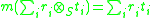is an R-R-bimodule epimorphism, which is split as an R-S-bimodule epi by the right inverse mapping 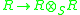given by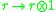. If R is a separable extension over S, then the multiplication mapping is split as an R-R-bimodule epi, so there is a right inverse s of m satisfying for s(1) := e, re = er for all r in R, and m(e) = 1. Conversely, if such an element (called a separability element in the tensor-square) exists, one shows by a judicious use of this element (like Maschke, applying its components within and without the splitting maps) that R is a separable extension of S.Equivalently, the relative Hochschild cohomology groups
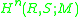of (R,S) in any coefficient bimodule M is zero for n > 0. Examples of separable extensions are many including first separable algebras where R = separable algebra and S = 1 times the ground field. More interestingly, any ring R with elements a and b satisfying ab = 1, but ba different from 1, is a separable extension over the subring S generated by 1 and bRa.An interesting theorem in the area is that of J. Cuadra that a separable Hopf-Galois extension R | S has finitely generated natural S-module R. A fundamental fact about a separable extension R | S is that it is left or right semisimple extension: a short exact sequence of left or right R-modules that is split as S-modules, is split as R-modules. In terms of G. Hochschild's relative homological algebra, one says that all R-modules are relative (R,S)-projective. Usually relative properties of subrings or ring extensions, such as the notion of separable extension, serve to promote theorems that say that the over-ring shares a property of the subring. For example, a separable extension R of a semisimple algebra S has R semisimple, which follows from the preceding discussion.
There is the celebrated Jans theorem that a finite group algebra A over a field of
characteristic p is of finite representation type if and only if its Sylow p-subgroup is cyclic: the clearest proof is to note this fact for p-groups, then note that the group algebra is a separable extension of its Sylow p-subgroup algebra B as the index is coprime to the characteristic. The separability condition above will imply every finitely generated A-module M is isomorphic to a direct summand
in its restricted, induced module. But if B has finite representation type, the restricted module
is uniquely a direct sum of multiples of finitely many indecomposables, which induce to a finite number of constituent indecomposable modules of which M is a direct sum. Hence A is of finite representation type if B is. The converse if proven by a similar argument noting that every subgroup algebra B is a B-bimodule direct summand of a group algebra A.