Sequential quadratic programming
Encyclopedia
Sequential quadratic programming (SQP) is an iterative method for nonlinear optimization
. SQP methods are used on problems for which the objective function and the constraints are twice continuously differentiable.
SQP methods solve a sequence of optimization subproblems, each which optimizes a quadratic model of the objective subject to a linearization of the constraints. If the problem is unconstrained, then the method reduces to Newton's method
for finding a point where the gradient of the objective vanishes. If the problem has only equality constraints, then the method is equivalent to applying Newton's method
to the first-order optimality conditions, or Karush–Kuhn–Tucker conditions, of the problem. SQP methods have been implemented in a many packages, including NPSOL
, NLPQL, OPSYC, OPTIMA
, MATLAB
, and SQP
.
problem of the form:
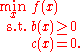
The Lagrangian for this problem is
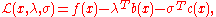
where
and 
are Lagrange multipliers
. At an iterate
, a basic sequential quadratic programming algorithm defines an appropriate search direction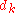 
as a solution to the quadratic programming
subproblem
Nonlinear programming
In mathematics, nonlinear programming is the process of solving a system of equalities and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function to be maximized or minimized, where some of the constraints or the objective function are...
. SQP methods are used on problems for which the objective function and the constraints are twice continuously differentiable.
SQP methods solve a sequence of optimization subproblems, each which optimizes a quadratic model of the objective subject to a linearization of the constraints. If the problem is unconstrained, then the method reduces to Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
for finding a point where the gradient of the objective vanishes. If the problem has only equality constraints, then the method is equivalent to applying Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
to the first-order optimality conditions, or Karush–Kuhn–Tucker conditions, of the problem. SQP methods have been implemented in a many packages, including NPSOL
NPSOL
NPSOL is a software package that performs numerical optimization. It solves nonlinear constrained problems using the sequential quadratic programming algorithm. It was written in Fortran by Philip Gill of UCSD and Walter Murray, Michael Saunders and Margaret Wright of Stanford University...
, NLPQL, OPSYC, OPTIMA
Optima
Optima is a humanist sans-serif typeface designed by Hermann Zapf between 1952 and 1955 for the D. Stempel AG foundry, Frankfurt, Germany.-Characteristics:...
, MATLAB
MATLAB
MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
, and SQP
SQP
SQP is a three-letter abbreviation with multiple meanings, as described below:* Sequential quadratic programming* the peer-reviewed journal Software Quality Professional...
.
Algorithm basics
Consider a nonlinear programmingNonlinear programming
In mathematics, nonlinear programming is the process of solving a system of equalities and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function to be maximized or minimized, where some of the constraints or the objective function are...
problem of the form:
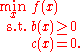
The Lagrangian for this problem is
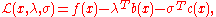
where
and are Lagrange multipliersLagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
. At an iterate
, a basic sequential quadratic programming algorithm defines an appropriate search direction 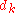as a solution to the quadratic programmingQuadratic programming
Quadratic programming is a special type of mathematical optimization problem. It is the problem of optimizing a quadratic function of several variables subject to linear constraints on these variables....
subproblem