Shelah cardinal
Encyclopedia
In axiomatic set theory, Shelah cardinals are a kind of large cardinals. A cardinal
is called Shelah iff
for every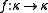
, there exists a transitive class 
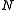and an elementary embedding 
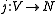with critical point
; and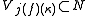 
.
A Shelah cardinal has a normal ultrafilter
containing the set of weakly hyper-Woodin cardinals below it.
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
is called Shelah iffIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
for every
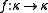, there exists a transitive class 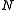and an elementary embedding 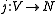with critical pointCritical point (set theory)
In set theory, the critical point of an elementary embedding of a transitive class into another transitive class is the smallest ordinal which is not mapped to itself....
; and 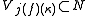.A Shelah cardinal has a normal ultrafilter
Ultrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
containing the set of weakly hyper-Woodin cardinals below it.