Short supermultiplet
Encyclopedia
In theoretical physics
, a short supermultiplet is a supermultiplet
i.e. a representation of the supersymmetry
algebra whose dimension is smaller than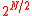
where 
is the number of real supercharges. The representations that saturate the bound are known as the long supermultiplets.
The states in a long supermultiplets may be produced from a representative by the action of the lowering and raising operators, assuming that for any basis vector, either the lowering operator or its conjugate raising operator produce a new nonzero state. This is the reason for the dimension indicated above. On the other hand, the short supermultiplets admit a subset of supercharges that annihilate the whole representation. That is why the short supermultiplets contain the BPS state
s, another description of the same concept.
The BPS states are only possible for objects that are either massless or massive extremal, i.e. carrying a maximum allowed value of some central charge
s.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, a short supermultiplet is a supermultiplet
Supermultiplet
In theoretical physics, a supermultiplet is formally a group representation of a supersymmetry algebra. It consists of a collection of particles, called superpartners, corresponding to operators in a quantum field theory which in superspace are represented by superfields.Superfields were...
i.e. a representation of the supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
algebra whose dimension is smaller than
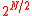where is the number of real supercharges. The representations that saturate the bound are known as the long supermultiplets.The states in a long supermultiplets may be produced from a representative by the action of the lowering and raising operators, assuming that for any basis vector, either the lowering operator or its conjugate raising operator produce a new nonzero state. This is the reason for the dimension indicated above. On the other hand, the short supermultiplets admit a subset of supercharges that annihilate the whole representation. That is why the short supermultiplets contain the BPS state
BPS state
In theoretical physics, BPS states are massive representations of an extended supersymmetry algebra with mass equal to the supersymmetry central charge Z. Quantum mechanically, if the supersymmetry does not get broken, the mass is exactly equal to the modulus of Z...
s, another description of the same concept.
The BPS states are only possible for objects that are either massless or massive extremal, i.e. carrying a maximum allowed value of some central charge
Central charge
In theoretical physics, a central charge is an operator Z that commutes with all the other symmetry operators. The adjective "central" refers to the center of the symmetry group -- the subgroup of elements that commute with all other elements of the original group—or to the center of a Lie algebra...
s.