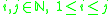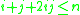Sieve of Sundaram
Encyclopedia
In mathematics
, the sieve of Sundaram is a simple deterministic algorithm
for finding all prime number
s up to a specified integer. It was discovered in 1934 by S. P. Sundaram, an Indian student from Sathyamangalam
.
The remaining numbers are doubled and incremented by one, giving a list of the odd prime numbers (i.e., all primes except 2) below 2n + 2.
The sieve of Sundaram sieves out the composite numbers just as sieve of Eratosthenes
does, but even numbers are not considered; the work of "crossing out" the multiples of 2 is done by the final double-and-increment step. Whenever Eratosthenes' method would cross out k different multiples of a prime 2i+1, Sundaram's method crosses out i + j(2i+1) for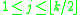 .
.
An odd integer is excluded from the final list if and only if
it is of the form 2(i + j + 2ij) + 1, and we have
So, an odd integer is excluded from the final list if and only if it has a factorization of the form (2i + 1)(2j + 1) — which is to say, if it has a non-trivial odd factor. Since every odd composite number has a non-trivial odd factor, we may safely say that an odd integer is excluded from the final list if and only if it is composite. Therefore the list must be composed of exactly the set of odd prime numbers less than or equal to n.
(n log n) operations using Θ(n) bits of memory.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the sieve of Sundaram is a simple deterministic algorithm
Deterministic algorithm
In computer science, a deterministic algorithm is an algorithm which, in informal terms, behaves predictably. Given a particular input, it will always produce the same output, and the underlying machine will always pass through the same sequence of states...
for finding all prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s up to a specified integer. It was discovered in 1934 by S. P. Sundaram, an Indian student from Sathyamangalam
Sathyamangalam
Sathyamangalam or Sathy is a small city and taluk in Erode district in the Indian state of Tamil Nadu. It lies on both banks of the Bhavani River, a tributary of the Kaveri in the foothills of the Western Ghats...
.
Algorithm
Start with a list of the integers from 1 to n. From this list, remove all numbers of the form i + j + 2ij where:The remaining numbers are doubled and incremented by one, giving a list of the odd prime numbers (i.e., all primes except 2) below 2n + 2.
The sieve of Sundaram sieves out the composite numbers just as sieve of Eratosthenes
Sieve of Eratosthenes
In mathematics, the sieve of Eratosthenes , one of a number of prime number sieves, is a simple, ancient algorithm for finding all prime numbers up to a specified integer....
does, but even numbers are not considered; the work of "crossing out" the multiples of 2 is done by the final double-and-increment step. Whenever Eratosthenes' method would cross out k different multiples of a prime 2i+1, Sundaram's method crosses out i + j(2i+1) for
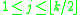 .
.Correctness
The final list of doubled-and-incremented integers contains only odd integers; we must show that the set of odd integers excluded from the list is exactly the set of composite odd integers.An odd integer is excluded from the final list if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is of the form 2(i + j + 2ij) + 1, and we have
- 2(i + j + 2ij) + 1
- = 2i + 2j + 4ij + 1
- = (2i + 1)(2j + 1).
So, an odd integer is excluded from the final list if and only if it has a factorization of the form (2i + 1)(2j + 1) — which is to say, if it has a non-trivial odd factor. Since every odd composite number has a non-trivial odd factor, we may safely say that an odd integer is excluded from the final list if and only if it is composite. Therefore the list must be composed of exactly the set of odd prime numbers less than or equal to n.
Computational complexity
The sieve of Sundaram finds the primes less than n in ΘBig O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n log n) operations using Θ(n) bits of memory.