
Sigma-ideal
Encyclopedia
In mathematics
, particularly measure theory, a σ-ideal of a sigma-algebra
(σ, read "sigma," means countable in this context) is a subset
with certain desirable closure
properties. It is a special type of ideal
. Its most frequent application is perhaps in probability theory
.
Let (X,Σ) be a measurable space (meaning Σ is a σ-algebra of subsets of X). A subset N of Σ is a σ-ideal if the following properties are satisfied:
(i) Ø ∈ N;
(ii) When A ∈ N and B ∈ Σ , B ⊆ A ⇒ B ∈ N;
(iii)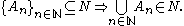
Briefly, a sigma-ideal must contain the empty set and contain subsets and countable unions of its elements. The concept of σ-ideal is dual
to that of a countably complete
(σ-) filter
.
If a measure
μ is given on (X,Σ), the set of μ-negligible set
s (S ∈ Σ such that μ(S) = 0) is a σ-ideal.
The notion can be generalized to preorder
s (P,≤,0) with a bottom element 0 as follows: I is a σ-ideal of P just when
(i') 0 ∈ I,
(ii') x ≤ y & y ∈ I ⇒ x ∈ I, and
(iii') given a family xn ∈ I (n ∈ N), there is y ∈ I such that xn ≤ y for each n
Thus I contains the bottom element, is downward closed, and is closed under countable suprema (which must exist). It is natural in this context to ask that P itself have countable suprema.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly measure theory, a σ-ideal of a sigma-algebra
Sigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
(σ, read "sigma," means countable in this context) is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
with certain desirable closure
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
properties. It is a special type of ideal
Ideal (set theory)
In the mathematical field of set theory, an ideal is a collection of sets that are considered to be "small" or "negligible". Every subset of an element of the ideal must also be in the ideal , and the union of any two elements of the ideal must also be in the ideal.More formally, given a set X, an...
. Its most frequent application is perhaps in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
.
Let (X,Σ) be a measurable space (meaning Σ is a σ-algebra of subsets of X). A subset N of Σ is a σ-ideal if the following properties are satisfied:
(i) Ø ∈ N;
(ii) When A ∈ N and B ∈ Σ , B ⊆ A ⇒ B ∈ N;
(iii)
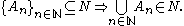
Briefly, a sigma-ideal must contain the empty set and contain subsets and countable unions of its elements. The concept of σ-ideal is dual
Duality (order theory)
In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...
to that of a countably complete
Completeness (order theory)
In the mathematical area of order theory, completeness properties assert the existence of certain infima or suprema of a given partially ordered set . A special use of the term refers to complete partial orders or complete lattices...
(σ-) filter
Filter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
.
If a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
μ is given on (X,Σ), the set of μ-negligible set
Negligible set
In mathematics, a negligible set is a set that is small enough that it can be ignored for some purpose.As common examples, finite sets can be ignored when studying the limit of a sequence, and null sets can be ignored when studying the integral of a measurable function.Negligible sets define...
s (S ∈ Σ such that μ(S) = 0) is a σ-ideal.
The notion can be generalized to preorder
Preorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
s (P,≤,0) with a bottom element 0 as follows: I is a σ-ideal of P just when
(i') 0 ∈ I,
(ii') x ≤ y & y ∈ I ⇒ x ∈ I, and
(iii') given a family xn ∈ I (n ∈ N), there is y ∈ I such that xn ≤ y for each n
Thus I contains the bottom element, is downward closed, and is closed under countable suprema (which must exist). It is natural in this context to ask that P itself have countable suprema.

