
Sigma approximation
Encyclopedia
In mathematics
, σ-approximation adjusts a Fourier summation
to eliminate the Gibbs phenomenon
which would otherwise occur at discontinuities.
A σ-approximated summation for a series of period T can be written as follows:
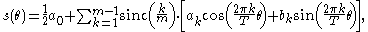
in terms of the normalized sinc function
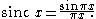
Here, the term
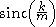
is the Lanczos σ factor, which is responsible for eliminating most of the Gibbs phenomenon. It does not do so entirely, however, but one can square or even cube the expression to serially attenuate Gibbs Phenomenon in the most extreme cases.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, σ-approximation adjusts a Fourier summation
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
to eliminate the Gibbs phenomenon
Gibbs phenomenon
In mathematics, the Gibbs phenomenon, named after the American physicist J. Willard Gibbs, is the peculiar manner in which the Fourier series of a piecewise continuously differentiable periodic function behaves at a jump discontinuity: the nth partial sum of the Fourier series has large...
which would otherwise occur at discontinuities.
A σ-approximated summation for a series of period T can be written as follows:
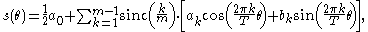
in terms of the normalized sinc function
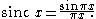
Here, the term
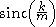
is the Lanczos σ factor, which is responsible for eliminating most of the Gibbs phenomenon. It does not do so entirely, however, but one can square or even cube the expression to serially attenuate Gibbs Phenomenon in the most extreme cases.

