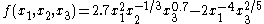Signomial
Encyclopedia
A "signomial" is an algebraic function
of one or more independent variables. It is perhaps most easily thought of as an algebraic extension of multi-dimensional polynomial
s -- an extension that permits exponents to be arbitrary real numbers (rather than just non-negative integers) while requiring the independent variables to be strictly positive (so that division by zero and other inappropriate algebraic operations are not encountered).
Formally, let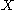
be a vector of real, positive numbers.
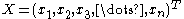
Then a signomial function has the form
where the coefficients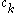
and the exponents 
are real numbers. Signomials are closed
under addition, subtraction, multiplication, and scaling.
If we restrict all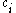
to be positive, then the function f is a posynomial. Consequently, each signomial is either a posynomial, the negative of a posynomial, or the difference of two posynomials. If, in addition, all exponents 
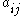are non-negative integers, then the signomial becomes a polynomial
whose domain is the positive orthant
.
For example,
is a signomial.
The term "signomial" was introduced by Richard J. Duffin and Elmor L. Peterson in their seminal joint work on general algebraic optimization -- published in the late 1960's and early 1970's. A recent introductory exposition is optimization problem
s. Although nonlinear optimization problems with constraints and/or objectives defined by signomials are normally harder to solve than those defined by only posynomials (because, unlike posynomials, signomials are not guaranteed to be globally convex), signomial optimization problems often provide a much more accurate mathematical representation of real-world nonlinear optimization problems.
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of one or more independent variables. It is perhaps most easily thought of as an algebraic extension of multi-dimensional polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s -- an extension that permits exponents to be arbitrary real numbers (rather than just non-negative integers) while requiring the independent variables to be strictly positive (so that division by zero and other inappropriate algebraic operations are not encountered).
Formally, let
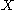be a vector of real, positive numbers.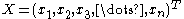Then a signomial function has the form
where the coefficients
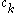and the exponents are real numbers. Signomials are closedClosure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under addition, subtraction, multiplication, and scaling.
If we restrict all
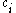to be positive, then the function f is a posynomial. Consequently, each signomial is either a posynomial, the negative of a posynomial, or the difference of two posynomials. If, in addition, all exponents 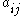are non-negative integers, then the signomial becomes a polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
whose domain is the positive orthant
Orthant
In geometry, an orthant or hyperoctant is the analogue in n-dimensional Euclidean space of a quadrant in the plane or an octant in three dimensions....
.
For example,
is a signomial.
The term "signomial" was introduced by Richard J. Duffin and Elmor L. Peterson in their seminal joint work on general algebraic optimization -- published in the late 1960's and early 1970's. A recent introductory exposition is optimization problem
Optimization problem
In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
s. Although nonlinear optimization problems with constraints and/or objectives defined by signomials are normally harder to solve than those defined by only posynomials (because, unlike posynomials, signomials are not guaranteed to be globally convex), signomial optimization problems often provide a much more accurate mathematical representation of real-world nonlinear optimization problems.
External links
- S. Boyd, S. J. Kim, L. Vandenberghe, and A. Hassibi, A Tutorial on Geometric Programming