Simon's algorithm
Encyclopedia
Simon's algorithm, conceived by Daniel Simon in 1994, is a quantum algorithm
which solves a black-box problem exponentially faster than any classical algorithm, including probabilistic algorithms. The algorithm uses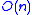
queries to the black box, whereas the best classical randomized algorithm necessarily needs at least 
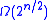queries.
It is also known that Simon's algorithm is optimal in the sense that any quantum algorithm to solve this problem requires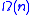
queries.
We have a random oracle
relative to which BPP and BQP
are separated. This is an improvement over the Deutsch-Jozsa algorithm
separating P
from EQP. The oracle needs to be quantum and nondecohering.
The input to the problem is a function (implemented by a black box)
, promised to satisfy the property that for some 
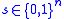we have for all 
, 
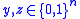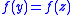if and only if 
or 
. Note that the case of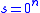 
is allowed, and corresponds to 
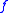being a permutation. The problem then is to find s.
The set of n-bit strings is a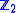
vector space under bitwise XOR. Given the promise, the preimage of f is either empty, or forms coset
s with n-1 dimensions. Using quantum algorithms, we can, with arbitrarily high probability determine the basis vectors spanning this n-1 subspace since s is a vector orthogonal to all of the basis vectors.
Consider the Hilbert space
consisting of the tensor product of the Hilbert space of input strings, and output strings. Using Hadamard operations, we can prepare the initial state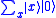
and then call the oracle to transform this state to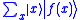
Hadamard transforms convert this state to
We perform a simultaneous measurement of both registers. If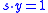
, we have destructive interference. So, only the subspace 
is picked out. Given enough samples of y, we can figure out the n-1 basis vectors, and compute s.
Although the problem itself is of little practical value it is interesting because it provides an exponential speedup over any classical algorithm. Moreover, it was also the inspiration for Shor's algorithm
. Both problems are special cases of the abelian hidden subgroup problem
, which is now known to have efficient quantum algorithms.
Quantum algorithm
In quantum computing, a quantum algorithm is an algorithm which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a...
which solves a black-box problem exponentially faster than any classical algorithm, including probabilistic algorithms. The algorithm uses
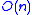queries to the black box, whereas the best classical randomized algorithm necessarily needs at least 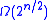queries.It is also known that Simon's algorithm is optimal in the sense that any quantum algorithm to solve this problem requires
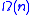queries.We have a random oracle
Random oracle
In cryptography, a random oracle is an oracle that responds to every query with a random response chosen uniformly from its output domain, except that for any specific query, it responds the same way every time it receives that query...
relative to which BPP and BQP
BQP
In computational complexity theory BQP is the class of decision problems solvable by a quantum computer in polynomial time, with an error probability of at most 1/3 for all instances...
are separated. This is an improvement over the Deutsch-Jozsa algorithm
Deutsch-Jozsa algorithm
The Deutsch–Jozsa algorithm is a quantum algorithm, proposed by David Deutsch and Richard Jozsa in 1992 with improvements by Richard Cleve, Artur Ekert, Chiara Macchiavello, and Michele Mosca in 1998...
separating P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
from EQP. The oracle needs to be quantum and nondecohering.
The input to the problem is a function (implemented by a black box)
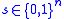, promised to satisfy the property that for some we have for all 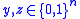, 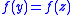if and only if or . Note that the case of 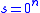is allowed, and corresponds to 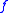being a permutation. The problem then is to find s.The set of n-bit strings is a
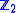vector space under bitwise XOR. Given the promise, the preimage of f is either empty, or forms cosetCoset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s with n-1 dimensions. Using quantum algorithms, we can, with arbitrarily high probability determine the basis vectors spanning this n-1 subspace since s is a vector orthogonal to all of the basis vectors.
Consider the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
consisting of the tensor product of the Hilbert space of input strings, and output strings. Using Hadamard operations, we can prepare the initial state
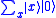
and then call the oracle to transform this state to
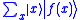
Hadamard transforms convert this state to
We perform a simultaneous measurement of both registers. If
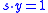, we have destructive interference. So, only the subspace is picked out. Given enough samples of y, we can figure out the n-1 basis vectors, and compute s.Although the problem itself is of little practical value it is interesting because it provides an exponential speedup over any classical algorithm. Moreover, it was also the inspiration for Shor's algorithm
Shor's algorithm
Shor's algorithm, named after mathematician Peter Shor, is a quantum algorithm for integer factorization formulated in 1994...
. Both problems are special cases of the abelian hidden subgroup problem
Hidden subgroup problem
The hidden subgroup problem is a topic of research in mathematics and theoretical computer science.-Problem statement:Given a group G, a subgroup H ≤ G, and a set X, we say a function f : G → X hides the subgroup H if for all g1, g2 ∈ G,f = f if and only if g1H = g2H for the cosets of...
, which is now known to have efficient quantum algorithms.