
Simson line
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
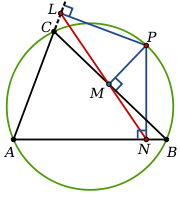
, given a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
ABC and a point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
P on its circumcircle, the three closest points to P on lines AB, AC, and BC are collinear. The line through these points is the Simson line of P, named for Robert Simson
Robert Simson
Robert Simson was a Scottish mathematician and professor of mathematics at the University of Glasgow. The pedal line of a triangle is sometimes called the "Simson line" after him.-Life:...
. The concept was first published, however, by William Wallace
William Wallace (mathematician)
William Wallace was a Scottish mathematician and astronomer who invented the eidograph.-Biography:Wallace was born at Dysart in Fife, where he received his school education...
.
The converse is also true; if the three closest points to P on three lines are collinear, and no two of the lines are parallel, then P lies on the circumcircle of the triangle formed by the three lines. The Simson line of a triangle ABC and a point P is just the pedal triangle
Pedal triangle
In geometry, a pedal triangle is obtained by projecting a point onto the sides of a triangle.More specifically, consider a triangle ABC, and a point P that is not one of the vertices A, B, C. Drop perpendiculars from P to the three sides of the triangle...
of ABC and P, in the case when that pedal triangle degenerates to a line.
Properties
- The Simson line of a vertex of the triangle is the altitude of the triangle dropped from that vertex, and the Simson line of the point diametrically opposite to the vertex is the side of the triangle opposite to that vertex.
- If
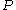 and
and  ' are points on the circumcircle, then the angle between the Simson lines of
' are points on the circumcircle, then the angle between the Simson lines of 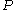 and
and 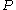 ' is half the angle of the arc
' is half the angle of the arc 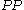 '. In particular, if the points are diametrically opposite, their Simson lines are perpendicular and in this case the intersection of the lines is on the nine-point circleNine-point circleIn geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant points defined from the triangle...
'. In particular, if the points are diametrically opposite, their Simson lines are perpendicular and in this case the intersection of the lines is on the nine-point circleNine-point circleIn geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant points defined from the triangle...
.
- Let
 denote the orthocenter of the triangle
denote the orthocenter of the triangle 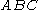 , then the Simson line of
, then the Simson line of 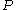 bisects the segment
bisects the segment  in a point that lies on the nine-point circle.
in a point that lies on the nine-point circle.
- Given two triangles with the same circumcircle, the angle between the Simson lines of a point
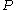 on the circumcircle for both triangles doesn't depend of
on the circumcircle for both triangles doesn't depend of  .
.
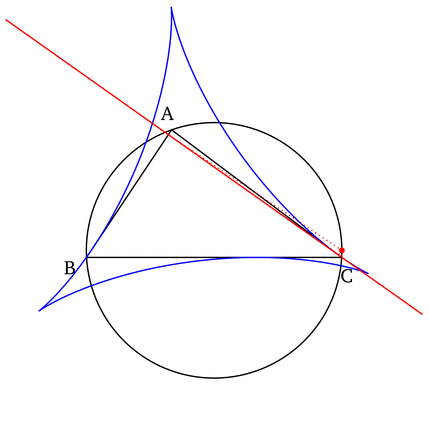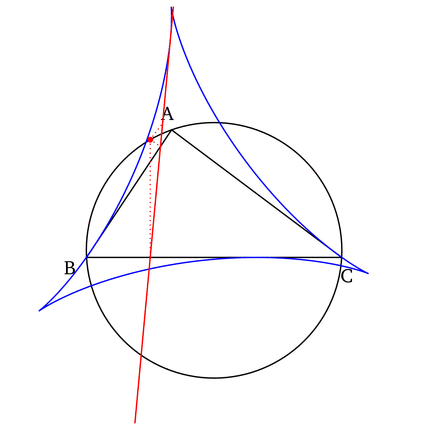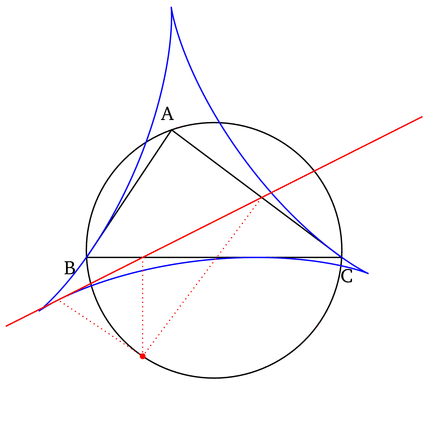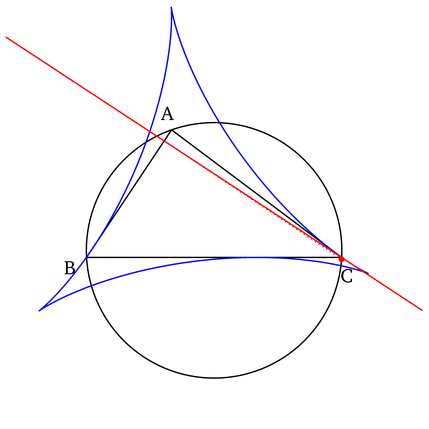
- The set of all Simson lines, when drawn, form an envelopeEnvelope (mathematics)In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...
in the shape of a deltoid known as the Steiner deltoid of the reference triangle.
- The construction of the Simson line that coincides with a side of the reference triangle (see first property above) yields a non trivial point on this side line. This point is the reflection of the foot of the altitude (dropped onto the side line) about the midpoint of the side line being constructed. Furthermore this point is a tangent point between the side of the reference triangle and its Steiner deltoid.
Proof of existence
The method of proof is to show that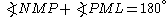 .
.  is a cyclic quadrilateral, so
is a cyclic quadrilateral, so 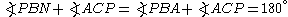 .
. 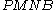 is a cyclic quadrilateral (Thales' theorem
is a cyclic quadrilateral (Thales' theoremThales' theorem
In geometry, Thales' theorem states that if A, B and C are points on a circle where the line AC is a diameter of the circle, then the angle ABC is a right angle. Thales' theorem is a special case of the inscribed angle theorem...
), so
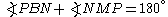 . Hence
. Hence 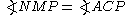 . Now
. Now 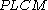 is cyclic, so
is cyclic, so  . Therefore
. Therefore  .
.
