
Pedal triangle
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a pedal triangle is obtained by projecting a point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
onto the sides of a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
.
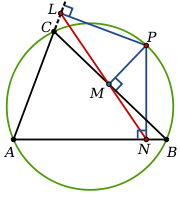
More specifically, consider a triangle ABC, and a point P that is not one of the vertices A, B, C. Drop perpendiculars from P to the three sides of the triangle (these may need to be produced, i.e., extended). Label L, M, N the intersections of the lines from P with the sides BC, AC, AB. The pedal triangle is then LMN.
The location of the chosen point P relative to the chosen triangle ABC gives rise to some special cases:
- If P = orthocenter, then LMN = orthic triangle.
- If P = incenter, then LMN = intouch triangle.
Simson line
In geometry, given a triangle ABC and a point P on its circumcircle, the three closest points to P on lines AB, AC, and BC are collinear. The line through these points is the Simson line of P, named for Robert Simson...
after Robert Simson
Robert Simson
Robert Simson was a Scottish mathematician and professor of mathematics at the University of Glasgow. The pedal line of a triangle is sometimes called the "Simson line" after him.-Life:...
.
If P has trilinear coordinates
Trilinear coordinates
In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
p : q : r, then the vertices L,M,N of the pedal triangle of P are given by
- L = 0 : q + p cos C : r + p cos B
- M = p + q cos C : 0 : r + q cos A
- N = p + r cos B : q + r cos A : 0
The A-vertex, L, of the antipedal triangle of P is the point of intersection of the perpendicular to BP through B and the perpendicular to CP through C. The B-vertex, M ', and the C-vertex, N ', are constructed analogously. Trilinear coordinates
Trilinear coordinates
In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
are given by
For example, the excentral triangle is the antipedal triangle of the incenter.
Suppose that P does not lie on a sideline, BC, CA, AB, and let P - 1 denote the isogonal conjugate
Isogonal conjugate
In geometry, the isogonal conjugate of a point P with respect to a triangle ABC is constructed by reflecting the lines PA, PB, and PC about the angle bisectors of A, B, and C. These three reflected lines concur at the isogonal conjugate of P...
of P. The pedal triangle of P is homothetic to the antipedal triangle of P - 1. The homothetic center (which is a triangle center if and only if P is a triangle center) is the point given in trilinear coordinates
Trilinear coordinates
In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
by
- ap(p + q cos C)(p + r cos B) : bq(q + r cos A)(q + p cos C) : cr(r + p cos B)(r + q cos A).
Another theorem about the pedal triangle of P and the antipedal triangle of P - 1 is that the product of their areas equals the square of the area of triangle ABC.
The point from which perpendiculars are drawn should be orthocentre then and only then it will be called as pedal triangle.

