
Skew-Hermitian
Encyclopedia
An anti-Hermitian, skew-Hermitian, or skew-adjoint operator or matrix
is one whose adjoint is the negative of itself:
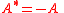
Imaginary number
s can be thought of as skew-adjoint (since they are like 1-by-1 matrices), whereas real number
s correspond to self-adjoint
operators.
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
is one whose adjoint is the negative of itself:
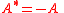
Imaginary number
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
s can be thought of as skew-adjoint (since they are like 1-by-1 matrices), whereas real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s correspond to self-adjoint
Self-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
operators.

