
Skinny triangle
Encyclopedia
A skinny triangle in trigonometry
is a triangle whose height is much greater than its base. The solution
of such triangles can be greatly simplified by using the approximation that the sine
of a small angle is equal to the angle in radian
s. The solution is particularly simple for skinny triangles that are also isosceles or right triangle
s: in these cases the need for trigonometric functions or tables can be entirely dispensed with.
The skinny triangle finds uses in surveying, astronomy and shooting.
The approximated solution to the skinny isosceles triangle, referring to figure 1, is;
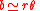
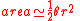
This is based on the small-angle approximations;

and,
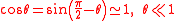
when is in radian
is in radian
s.
The proof of the skinny triangle solution follows from the small-angle approximation by applying the law of sines
. Again referring to figure 1;

The term represents the base angle of the triangle and is this value because the sum of the internal angles of any triangle (in this case the two base angles plus θ) are equal to π. Applying the small angle approximations to the law of sines above results in;
represents the base angle of the triangle and is this value because the sum of the internal angles of any triangle (in this case the two base angles plus θ) are equal to π. Applying the small angle approximations to the law of sines above results in;
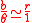
the desired result.
This result is equivalent to assuming that the length of the base of the triangle is equal to the length of the arc of circle of radius r subtended by angle θ. This approximation becomes ever more accurate for smaller and smaller θ. The error is 10% or less for angles less than about 43°.
The side-angle-side formula for the area of the triangle is;

Applying the small angle approximations results in;
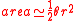
The approximated solution to the right skinny triangle, referring to figure 3, is;
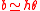
This is based on the small-angle approximation;
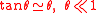
which when substituted into the exact solution;

yields the desired result.
The error of this approximation is less than 10% for angles 31° or less.
objects. The base of the triangle is formed by the distance between two measuring stations and the angle θ is the parallax
angle formed by the object as seen by the two stations. The baseline
is usually very long for best accuracy; in principle the stations could be on opposite sides of the Earth
. However, this distance is still short compared to the distance to the object being measured (the height of the triangle) and the skinny triangle solution can be applied and still achieve great accuracy. The alternative method of measuring the base angles is theoretically possible but not so accurate. The base angles are very nearly right angles and would need to be measured with much greater precision than the parallax angle in order to get the same accuracy.
The same method of measuring parallax angles and applying the skinny triangle can be used to measure the distances to stars; at least the nearer ones. In the case of stars however, a longer baseline than the diameter of the Earth is usually required. This can be achieved by instead of using two stations on the baseline, two measurements are made from the same station at different times of year. In the intervening period the orbit of the Earth around the Sun
moves the measuring station a great distance, so providing a very long baseline. This baseline can be as long as the major axis of the Earth's orbit or, equivalently, two Astronomical unit
s (AU). The distance to a star with a parallax angle of only one arcsecond measured on a baseline of one AU is a unit known as the parsec
(pc) in astronomy and is equal to about 3.26 light years. There is an inverse relationship between the distance in parsecs and the angle in arcseconds. For instance, two arcseconds corresponds to a distance of and 0.5 arcseconds corresponds to a distance of two parsecs.
s or mil-dots. A target in height and measuring in the sight corresponds to a range of 1000 metres. There is an inverse relationship between the angle measured in a sniper's sight and the distance to target. For instance, if this same target measures in the sight then the range is 500 metres.
Another unit which is sometimes used on gunsights is the minute of arc
(MOA). The distances corresponding to minutes of arc are not exact numbers in the metric system
as they are with milliradians, however, there is a convenient approximate whole number correspondence in imperial units. A target in height and measuring in the sight corresponds to a range of 100 yard
s.
, relies on making estimates of wind speeds aloft over long distances to calculate a desired heading. Since predicted or reported wind speeds are rarely accurate, corrections to the aircraft's heading need to be made at regular intervals. Skinny triangles form the basis of the 1 in 60 rule
, which is "After travelling 60 miles, your heading is one degree off for every mile you're off course". "60" is very close to 180 / π = 57.30.
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
is a triangle whose height is much greater than its base. The solution
Solution of triangles
In trigonometry, to solve a triangle is to find the three angles and the lengths of the three sides of the triangle when given some, but not all of that information...
of such triangles can be greatly simplified by using the approximation that the sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
of a small angle is equal to the angle in radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s. The solution is particularly simple for skinny triangles that are also isosceles or right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
s: in these cases the need for trigonometric functions or tables can be entirely dispensed with.
The skinny triangle finds uses in surveying, astronomy and shooting.
Isosceles triangle
| Large angles | Small angles | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
EWLINE
|
EWLINE
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The approximated solution to the skinny isosceles triangle, referring to figure 1, is;
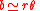
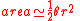
This is based on the small-angle approximations;

and,
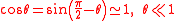
when
 is in radian
is in radianRadian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s.
The proof of the skinny triangle solution follows from the small-angle approximation by applying the law of sines
Law of sines
In trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...
. Again referring to figure 1;

The term
 represents the base angle of the triangle and is this value because the sum of the internal angles of any triangle (in this case the two base angles plus θ) are equal to π. Applying the small angle approximations to the law of sines above results in;
represents the base angle of the triangle and is this value because the sum of the internal angles of any triangle (in this case the two base angles plus θ) are equal to π. Applying the small angle approximations to the law of sines above results in;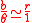
the desired result.
This result is equivalent to assuming that the length of the base of the triangle is equal to the length of the arc of circle of radius r subtended by angle θ. This approximation becomes ever more accurate for smaller and smaller θ. The error is 10% or less for angles less than about 43°.
The side-angle-side formula for the area of the triangle is;

Applying the small angle approximations results in;
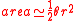
Right triangle
| Large angles | Small angles | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
EWLINE
|
EWLINE
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The approximated solution to the right skinny triangle, referring to figure 3, is;
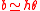
This is based on the small-angle approximation;
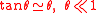
which when substituted into the exact solution;

yields the desired result.
The error of this approximation is less than 10% for angles 31° or less.
Applications
Applications of the skinny triangle occur in any situation where the distance to a far object is to be determined. This can occur in surveying, astronomy, and also has military applications.Astronomy
The skinny triangle is frequently used in astronomy to measure the distance to solar systemSolar System
The Solar System consists of the Sun and the astronomical objects gravitationally bound in orbit around it, all of which formed from the collapse of a giant molecular cloud approximately 4.6 billion years ago. The vast majority of the system's mass is in the Sun...
objects. The base of the triangle is formed by the distance between two measuring stations and the angle θ is the parallax
Parallax
Parallax is a displacement or difference in the apparent position of an object viewed along two different lines of sight, and is measured by the angle or semi-angle of inclination between those two lines. The term is derived from the Greek παράλλαξις , meaning "alteration"...
angle formed by the object as seen by the two stations. The baseline
Baseline
A baseline is a line that is a base for measurement or for construction; see datum or point of reference .The word baseline may refer to:...
is usually very long for best accuracy; in principle the stations could be on opposite sides of the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
. However, this distance is still short compared to the distance to the object being measured (the height of the triangle) and the skinny triangle solution can be applied and still achieve great accuracy. The alternative method of measuring the base angles is theoretically possible but not so accurate. The base angles are very nearly right angles and would need to be measured with much greater precision than the parallax angle in order to get the same accuracy.
The same method of measuring parallax angles and applying the skinny triangle can be used to measure the distances to stars; at least the nearer ones. In the case of stars however, a longer baseline than the diameter of the Earth is usually required. This can be achieved by instead of using two stations on the baseline, two measurements are made from the same station at different times of year. In the intervening period the orbit of the Earth around the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
moves the measuring station a great distance, so providing a very long baseline. This baseline can be as long as the major axis of the Earth's orbit or, equivalently, two Astronomical unit
Astronomical unit
An astronomical unit is a unit of length equal to about or approximately the mean Earth–Sun distance....
s (AU). The distance to a star with a parallax angle of only one arcsecond measured on a baseline of one AU is a unit known as the parsec
Parsec
The parsec is a unit of length used in astronomy. It is about 3.26 light-years, or just under 31 trillion kilometres ....
(pc) in astronomy and is equal to about 3.26 light years. There is an inverse relationship between the distance in parsecs and the angle in arcseconds. For instance, two arcseconds corresponds to a distance of and 0.5 arcseconds corresponds to a distance of two parsecs.
Gunnery
The skinny triangle is useful in gunnery in that it allows a relationship to be calculated between the range and size of the target without the shooter needing to compute or look up any trigonometric functions. Military and hunting telescopic sights often have a reticle calibrated in milliradians, in this context usually called just milAngular mil
An angular mil, also mil, is a unit of angle. All versions of the angular mil are approximately the same size as a trigonometric milliradian.-History:The milliradian was first identified in the mid nineteenth Century...
s or mil-dots. A target in height and measuring in the sight corresponds to a range of 1000 metres. There is an inverse relationship between the angle measured in a sniper's sight and the distance to target. For instance, if this same target measures in the sight then the range is 500 metres.
Another unit which is sometimes used on gunsights is the minute of arc
Minute of arc
A minute of arc, arcminute, or minute of angle , is a unit of angular measurement equal to one sixtieth of one degree. In turn, a second of arc or arcsecond is one sixtieth of one minute of arc....
(MOA). The distances corresponding to minutes of arc are not exact numbers in the metric system
Metric system
The metric system is an international decimalised system of measurement. France was first to adopt a metric system, in 1799, and a metric system is now the official system of measurement, used in almost every country in the world...
as they are with milliradians, however, there is a convenient approximate whole number correspondence in imperial units. A target in height and measuring in the sight corresponds to a range of 100 yard
Yard
A yard is a unit of length in several different systems including English units, Imperial units and United States customary units. It is equal to 3 feet or 36 inches...
s.
Aviation
A simple form of aviation navigation, dead reckoningDead reckoning
In navigation, dead reckoning is the process of calculating one's current position by using a previously determined position, or fix, and advancing that position based upon known or estimated speeds over elapsed time, and course...
, relies on making estimates of wind speeds aloft over long distances to calculate a desired heading. Since predicted or reported wind speeds are rarely accurate, corrections to the aircraft's heading need to be made at regular intervals. Skinny triangles form the basis of the 1 in 60 rule
1 in 60 rule
The 1 in 60 rule is used in air navigation, and states that if a pilot has travelled sixty miles then an error in track of one mile is approximately a 1° error. It is based on the small-angle approximation. In reality the error is 0.96° but this difference is trivial in air navigation. It is hard...
, which is "After travelling 60 miles, your heading is one degree off for every mile you're off course". "60" is very close to 180 / π = 57.30.
See also
- Infinitesimal oscillations of a pendulum

