Slope One
Encyclopedia
Slope One is a family of algorithms used for collaborative filtering
, introduced in a 2005 paper by Daniel Lemire and Anna Maclachlan. Arguably, it is the simplest form of non-trivial item-based collaborative filtering based on ratings. Their simplicity makes it especially easy to implement them efficiently while their accuracy is often on par with more complicated and computationally expensive algorithms. They have also been used as building blocks to improve other algorithms.
Example: Can we predict the rating an individual would give to the new Celine Dion album given that he gave the Beatles 5 out of 5?
In this context, item-based collaborative filtering predicts the ratings on one item based on the ratings on another item, typically using linear regression
(
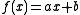). Hence, if there are 1,000 items, there could be up to 1,000,000 linear regressions to be learned, and so, up to 2,000,000 regressors. This approach may suffer from severe overfitting
unless we select only the pairs of items for which several users have rated both items.
A better alternative may be to learn a simpler predictor such as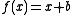
: experiments show that this simpler predictor (called Slope One) sometimes outperforms linear regression while having half the number of regressors. This simplified approach also reduces storage requirements and latency.
Item-based collaborative is just one form of collaborative filtering
. Other alternatives include user-based collaborative filtering where relationships between users are of interest, instead. However, item-based collaborative filtering is especially scalable with respect to the number of users.
rating-based algorithm do not apply.
Examples of binary item-based collaborative filtering include Amazon's item-to-item patented algorithm which computes the cosine between binary vectors representing the purchases in a user-item matrix.
Being arguably simpler than even Slope One, the Item-to-Item algorithm offers an interesting point of reference. Let us consider an example.
In this case, the cosine between items 1 and 2 is:
,
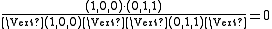The cosine between items 1 and 3 is:
,
Whereas the cosine between items 2 and 3 is:
.
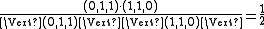Hence, a user visiting item 1 would receive item 3 as a recommendation, a user visiting item 2 would receive item 3 as a recommendation, and finally, a user visiting item 3 would receive item 1 (and then item 2) as a recommendation. The model uses a single parameter per pair of item (the cosine) to make the recommendation. Hence, if there are n items, up to n(n-1)/2 cosines need to be computed and stored.
, improve performance and ease implementation, the Slope One family of easily implemented Item-based Rating-Based collaborative filtering
algorithms was proposed. Essentially, instead of using linear regression from one item's ratings to another item's ratings (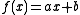
), it uses a simpler form of regression with a single free parameter (
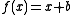). The free parameter is then simply the average difference between the two items' ratings. It was shown to be much more accurate than linear regression in some instances, and it takes half the storage or less.
Example:
For a more realistic example, consider the following table.
In this case, the average difference in ratings between item 2 and 1 is (2+(-1))/2=0.5. Hence, on average, item 1 is rated above item 2 by 0.5. Similarly, the average difference between item 3 and 1 is 3. Hence, if we attempt to predict the rating of Lucy for item 1 using her rating for item 2, we get 2+0.5 = 2.5. Similarly, if we try to predict her rating for item 1 using her rating of item 3, we get 5+3=8.
If a user rated several items, the predictions are simply combined using a weighted average where a good choice for the weight is the number of users having rated both items. In the above example, we would predict the following rating for Lucy on item 1:
Hence, given n items, to implement Slope One, all that is needed is to compute and store the average differences and the number of common ratings for each of the n2 pairs of items.
It is possible to reduce storage requirements by partitioning the data (see Partition (database)
) or by using sparse storage: pairs of items having no (or few) corating users can be omitted.
:
Ruby (programming language)
:
Java (programming language)
:
PHP
:
Erlang (programming language):
Haskell (programming language)
:
Visual Basic for Applications
:
C Sharp (programming language):
T-SQL:
R (programming language)
:
Clojure
:
Collaborative filtering
Collaborative filtering is the process of filtering for information or patterns using techniques involving collaboration among multiple agents, viewpoints, data sources, etc. Applications of collaborative filtering typically involve very large data sets...
, introduced in a 2005 paper by Daniel Lemire and Anna Maclachlan. Arguably, it is the simplest form of non-trivial item-based collaborative filtering based on ratings. Their simplicity makes it especially easy to implement them efficiently while their accuracy is often on par with more complicated and computationally expensive algorithms. They have also been used as building blocks to improve other algorithms.
Item-based collaborative filtering of rated resources and overfitting
When ratings of items are available, such as is the case when people are given the option of ratings resources (between 1 and 5, for example), collaborative filtering aims to predict the ratings of one individual based on his past ratings and on a (large) database of ratings contributed by other users.Example: Can we predict the rating an individual would give to the new Celine Dion album given that he gave the Beatles 5 out of 5?
In this context, item-based collaborative filtering predicts the ratings on one item based on the ratings on another item, typically using linear regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
(
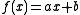). Hence, if there are 1,000 items, there could be up to 1,000,000 linear regressions to be learned, and so, up to 2,000,000 regressors. This approach may suffer from severe overfittingOverfitting
In statistics, overfitting occurs when a statistical model describes random error or noise instead of the underlying relationship. Overfitting generally occurs when a model is excessively complex, such as having too many parameters relative to the number of observations...
unless we select only the pairs of items for which several users have rated both items.
A better alternative may be to learn a simpler predictor such as
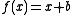: experiments show that this simpler predictor (called Slope One) sometimes outperforms linear regression while having half the number of regressors. This simplified approach also reduces storage requirements and latency.Item-based collaborative is just one form of collaborative filtering
Collaborative filtering
Collaborative filtering is the process of filtering for information or patterns using techniques involving collaboration among multiple agents, viewpoints, data sources, etc. Applications of collaborative filtering typically involve very large data sets...
. Other alternatives include user-based collaborative filtering where relationships between users are of interest, instead. However, item-based collaborative filtering is especially scalable with respect to the number of users.
Item-based collaborative filtering of purchase statistics
We are not always given ratings: when the users provide only binary data (the item was purchased or not), then Slope One and otherrating-based algorithm do not apply.
Examples of binary item-based collaborative filtering include Amazon's item-to-item patented algorithm which computes the cosine between binary vectors representing the purchases in a user-item matrix.
Being arguably simpler than even Slope One, the Item-to-Item algorithm offers an interesting point of reference. Let us consider an example.
| Customer | Item 1 | Item 2 | Item 3 |
|---|---|---|---|
| John | Bought it | Didn't buy it | Bought it |
| Mark | Didn't buy it | Bought it | Bought it |
| Lucy | Didn't buy it | Bought it | Didn't buy it |
In this case, the cosine between items 1 and 2 is:
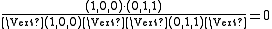,The cosine between items 1 and 3 is:
,Whereas the cosine between items 2 and 3 is:
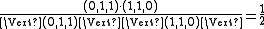.Hence, a user visiting item 1 would receive item 3 as a recommendation, a user visiting item 2 would receive item 3 as a recommendation, and finally, a user visiting item 3 would receive item 1 (and then item 2) as a recommendation. The model uses a single parameter per pair of item (the cosine) to make the recommendation. Hence, if there are n items, up to n(n-1)/2 cosines need to be computed and stored.
Slope one collaborative filtering for rated resources
To drastically reduce overfittingOverfitting
In statistics, overfitting occurs when a statistical model describes random error or noise instead of the underlying relationship. Overfitting generally occurs when a model is excessively complex, such as having too many parameters relative to the number of observations...
, improve performance and ease implementation, the Slope One family of easily implemented Item-based Rating-Based collaborative filtering
Collaborative filtering
Collaborative filtering is the process of filtering for information or patterns using techniques involving collaboration among multiple agents, viewpoints, data sources, etc. Applications of collaborative filtering typically involve very large data sets...
algorithms was proposed. Essentially, instead of using linear regression from one item's ratings to another item's ratings (
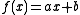), it uses a simpler form of regression with a single free parameter (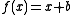). The free parameter is then simply the average difference between the two items' ratings. It was shown to be much more accurate than linear regression in some instances, and it takes half the storage or less.Example:
- User A gave a 1 to Item I and an 1.5 to Item J.
- User B gave a 2 to Item I.
- How do you think User B rated Item J?
- The Slope One answer is to say 2.5 (1.5-1+2=2.5).
For a more realistic example, consider the following table.
| Customer | Item 1 | Item 2 | Item 3 |
|---|---|---|---|
| John | 5 | 3 | 2 |
| Mark | 3 | 4 | Didn't rate it |
| Lucy | Didn't rate it | 2 | 5 |
In this case, the average difference in ratings between item 2 and 1 is (2+(-1))/2=0.5. Hence, on average, item 1 is rated above item 2 by 0.5. Similarly, the average difference between item 3 and 1 is 3. Hence, if we attempt to predict the rating of Lucy for item 1 using her rating for item 2, we get 2+0.5 = 2.5. Similarly, if we try to predict her rating for item 1 using her rating of item 3, we get 5+3=8.
If a user rated several items, the predictions are simply combined using a weighted average where a good choice for the weight is the number of users having rated both items. In the above example, we would predict the following rating for Lucy on item 1:
Hence, given n items, to implement Slope One, all that is needed is to compute and store the average differences and the number of common ratings for each of the n2 pairs of items.
Algorithmic complexity of Slope One
Suppose there are n items, m users, and N ratings. Computing the average rating differences for each pair of items requires up to n(n-1)/2 units of storage, and up to m n2 time steps. This computational bound may be pessimistic: if we assume that users have rated up to y items, then it is possible to compute the differences in no more than n2+my2. If a user has entered x ratings, predicting a single rating requires x time steps, and predicting all of his missing ratings requires up to (n-x)x time steps. Updating the database when a user has already entered x ratings, and enters a new one, requires x time steps.It is possible to reduce storage requirements by partitioning the data (see Partition (database)
Partition (database)
A partition is a division of a logical database or its constituting elements into distinct independent parts. Database partitioning is normally done for manageability, performance or availability reasons....
) or by using sparse storage: pairs of items having no (or few) corating users can be omitted.
Recommender systems using Slope One
- hitflip a DVD recommender system
- inDiscover an MP3 recommender system
- Value Investing News a stock market news site
- AllTheBests A shopping recommendation engine
- AllFamo eCommerce / Social media recommendation engine
- Qué libro me recomiendas a book recommender system (in Spanish)
Open source software implementing Slope One
Python (programming language)Python (programming language)
Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
:
- A well documented Python implementation together with a tutorial
Ruby (programming language)
Ruby (programming language)
Ruby is a dynamic, reflective, general-purpose object-oriented programming language that combines syntax inspired by Perl with Smalltalk-like features. Ruby originated in Japan during the mid-1990s and was first developed and designed by Yukihiro "Matz" Matsumoto...
:
- Ashley Williams implemented Slope One in Ruby.
Java (programming language)
Java (programming language)
Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
:
- Apache MahoutApache MahoutApache Mahout is an Apache project to produce free implementations of distributed or otherwise scalable machine learning algorithms on the Hadoop platform...
- LensKit
- A standalone Java class implementing Slope One.
- EasyrecEasyreceasyrec is an open source Web application that provides personalized recommendations using RESTful Web services to be integrated into Web enabled applications...
General purpose Open-Source SaaS recommender system / API
PHP
PHP
PHP is a general-purpose server-side scripting language originally designed for web development to produce dynamic web pages. For this purpose, PHP code is embedded into the HTML source document and interpreted by a web server with a PHP processor module, which generates the web page document...
:
- The Vogoo library supports Slope One algorithms (PHP)
- There is PHP source code accompanying a technical report on Slope One algorithms
- The OpenSlopeOne supports Slope One algorithms (PHP)
Erlang (programming language):
- Philip Robinson implemented Slope One in Erlang.
Haskell (programming language)
Haskell (programming language)
Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
:
- Bryan O'Sullivan implemented Slope One in Haskell.
Visual Basic for Applications
Visual Basic for Applications
Visual Basic for Applications is an implementation of Microsoft's event-driven programming language Visual Basic 6 and its associated integrated development environment , which are built into most Microsoft Office applications...
:
- A Microsoft ExcelMicrosoft ExcelMicrosoft Excel is a proprietary commercial spreadsheet application written and distributed by Microsoft for Microsoft Windows and Mac OS X. It features calculation, graphing tools, pivot tables, and a macro programming language called Visual Basic for Applications...
spreadsheet Slope One implementation using VBAVisual Basic for ApplicationsVisual Basic for Applications is an implementation of Microsoft's event-driven programming language Visual Basic 6 and its associated integrated development environment , which are built into most Microsoft Office applications...
(requires enabled macros).
C Sharp (programming language):
- The C# MyMediaLite Recommender System Library contains an implementation of Slope One.
- Kuber implemented Weighted Slope One in C#.
T-SQL:
- Charlie Zhu implemented Weighted Slope One in T-SQL.
R (programming language)
R (programming language)
R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
:
- Weighted Slope One in R
Clojure
Clojure
Clojure |closure]]") is a recent dialect of the Lisp programming language created by Rich Hickey. It is a general-purpose language supporting interactive development that encourages a functional programming style, and simplifies multithreaded programming....
:
- Weighted Slope One in Clojure