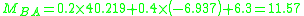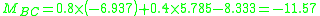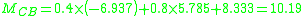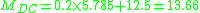
Slope deflection method
Encyclopedia
The slope deflection method is a structural analysis
method for beams
and frames introduced in 1915 by George A. Maney. The slope deflection method was widely used for more than a decade until the moment distribution method
was developed.
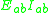and length 
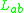are:
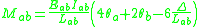
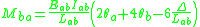
where
, 
are the slope angles of ends a and b respectively, 
is the relative lateral displacement of ends a and b. The absence of cross-sectional area of the member in these equations implies that the slope deflection method neglects the effect of shear and axial deformations.
The slope deflection equations can also be written using the stiffness factor
and the chord rotation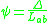 
:
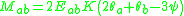
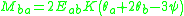
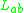and flexural rigidity 
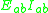is loaded at each end with counterclockwise moments 
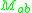and 
, member end rotations occur in the same direction. These rotation angles can be calculated using the unit dummy force method
or Darcy's Law
.
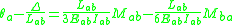
Rearranging these equations, the slope deflection equations are derived.
Here,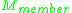
are the member end moments, 
are the fixed end moments, and 
are the external moments directly applied at the joint.
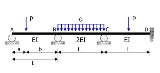
The statically indeterminate beam shown in the figure is to be analysed.
In the following calcuations, clockwise moments and rotations are positive.
, 
, 
, 
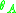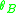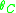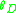of joints A, B, C, D respectively are taken as the unknowns. There are no chord rotations due to other causes including support settlement.
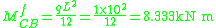
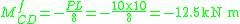
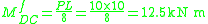
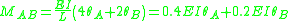
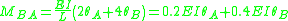
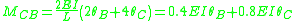
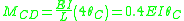
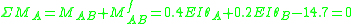
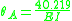
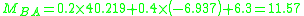
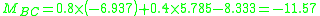
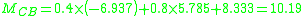
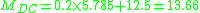
Structural analysis
Structural analysis is the determination of the effects of loads on physical structures and their components. Structures subject to this type of analysis include all that must withstand loads, such as buildings, bridges, vehicles, machinery, furniture, attire, soil strata, prostheses and...
method for beams
Beam (structure)
A beam is a horizontal structural element that is capable of withstanding load primarily by resisting bending. The bending force induced into the material of the beam as a result of the external loads, own weight, span and external reactions to these loads is called a bending moment.- Overview...
and frames introduced in 1915 by George A. Maney. The slope deflection method was widely used for more than a decade until the moment distribution method
Moment distribution method
The moment distribution method is a structural analysis method for statically indeterminate beams and frames developed by Hardy Cross. It was published in 1930 in an ASCE journal. The method only accounts for flexural effects and ignores axial and shear effects...
was developed.
Introduction
By forming slope deflection equations and applying joint and shear equilibrium conditions, the rotation angles (or the slope angles) are calculated. Substutituting them back into the slope deflection equations, member end moments are readily determined.Slope deflection equations
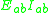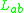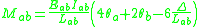
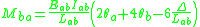
The slope deflection equations express the member end moments in terms of rotation angles. The slope deflection equations of member ab of flexural rigidity and length are:where
, are the slope angles of ends a and b respectively, is the relative lateral displacement of ends a and b. The absence of cross-sectional area of the member in these equations implies that the slope deflection method neglects the effect of shear and axial deformations.The slope deflection equations can also be written using the stiffness factor
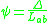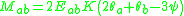
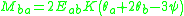
and the chord rotation :Derivation of slope deflection equations
When a simple beam of length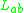 and flexural rigidity 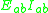is loaded at each end with counterclockwise moments 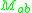and , member end rotations occur in the same direction. These rotation angles can be calculated using the unit dummy force methodUnit dummy force method
The Unit dummy force method provides a convenient means for computing displacements in structural systems. It is applicable for both linear and non-linear material behaviours as well as for systems subject to environmental effects, and hence more general than Castigliano's second theorem.-Discrete...
or Darcy's Law
Darcy's law
Darcy's law is a phenomenologically derived constitutive equation that describes the flow of a fluid through a porous medium. The law was formulated by Henry Darcy based on the results of experiments on the flow of water through beds of sand...
.
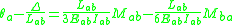
Rearranging these equations, the slope deflection equations are derived.
Joint equilibrium
Joint equilibrium conditions imply that each joint with a degree of freedom should have no unbalanced moments i.e. be in equilibrium. Therefore,Here,
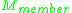are the member end moments, are the fixed end moments, and are the external moments directly applied at the joint.Shear equilibrium
When there are chord rotations in a frame, additional equilibrium conditions, namely the shear equilibrium conditions need to be taken into account.Example
- Members AB, BC, CD have the same length
. - Flexural rigidities are EI, 2EI, EI respectively.
- Concentrated load of magnitude
acts at a distance 
from the support A. - Uniform load of intensity
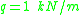acts on BC. - Member CD is loaded at its midspan with a concentrated load of magnitude
.
In the following calcuations, clockwise moments and rotations are positive.
Degrees of freedom
Rotation angles, , 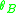, 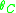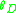of joints A, B, C, D respectively are taken as the unknowns. There are no chord rotations due to other causes including support settlement.Fixed end moments
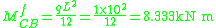
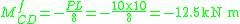
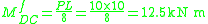
Fixed end moments are:Slope deflection equations
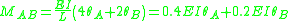
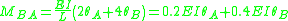
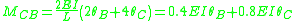
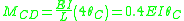
The slope deflection equations are constructed as follows:Joint equilibrium equations
Joints A, B, C should suffice the equilibrium condition. Therefore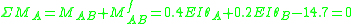Rotation angles
The rotation angles are calculated from simultaneous equations above.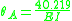Member end moments
Substitution of these values back into the slope deflection equations yields the member end moments (in kNm):