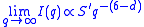Small-angle X-ray scattering
Encyclopedia
Small-angle X-ray scattering (SAXS) is a small-angle scattering
(SAS) technique where the elastic
scattering of X-ray
s (wavelength 0.1 ... 0.2 nm
) by a sample which has inhomogeneities in the nm-range, is recorded at very low angles (typically 0.1 - 10°). This angular range contains information about the shape and size of macromolecule
s, characteristic distances of partially ordered materials, pore sizes, and other data. SAXS is capable of delivering structural information of macromolecules between 5 and 25 nm, of repeat distances in partially ordered systems of up to 150 nm. USAXS (ultra-small angle X-ray scattering) can resolve even larger dimensions.
SAXS and USAXS belong to a family of X-ray scattering techniques
that are used in the characterization of materials. In the case of biologic macromolecule
s such as protein
s, the advantage of SAXS over crystallography
is that a crystalline sample is not needed. NMR
methods encounter problems with macromolecules of higher molecular mass (> 30000-40000). However, owing to the random orientation of dissolved or partially ordered molecules, the spatial averaging leads to a loss of information in SAXS compared to crystallography.
-like materials can be studied. The method is accurate, non-destructive and usually requires only a minimum of sample preparation. Applications are very broad and include colloid
s of all types, metals, cement, oil, polymer
s, plastics, proteins, foods and pharmaceuticals can be found in research as well as in quality control. The X-ray
source can be a laboratory source or synchrotron light
which provides a higher X-ray flux
.
of X-rays is brought to a sample from which some of the X-rays scatter, while most simply go through the sample without interacting with it. The scattered X-rays form a scattering pattern which is then detected at a detector which is typically a 2-dimensional flat X-ray detector situated behind the sample perpendicular to the direction of the primary beam that initially hit the sample. The scattering pattern contains the information on the structure of the sample.
The major problem that must be overcome in SAXS instrumentation is the separation of the weak scattered intensity from the strong main beam. The smaller the desired angle, the more difficult this becomes. The problem is comparable to one encountered when trying to observe a weakly radiant object close to the sun, like the sun's corona. Only if the moon blocks out the main light source does the corona become visible. Likewise, in SAXS the non-scattered beam that merely travels through the sample must be blocked, without blocking the closely adjacent scattered radiation. Most available X-ray sources produce divergent
beams and this compounds the problem. In principle the problem could be overcome by focusing
the beam, but this is not easy when dealing with X-rays and was previously not done except on synchrotron
s where large bent mirrors can be used. This is why most laboratory small angle devices rely on collimation
instead.
Laboratory SAXS instruments can be divided into two main groups: point-collimation and line-collimation instruments:
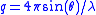. Here 
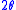is the angle between the incident X-ray beam and the detector measuring the scattered intensity, and 
is the wavelength of the X-rays. One interpretation of the scattering vector is that it is the resolution or yardstick with which the sample is observed. In the case of a two-phase sample, e.g. small particles in liquid suspension, the only contrast leading to scattering in the typical range of resolution of the SAXS is simply Δρ, the difference in average electron density between the particle and the surrounding liquid, because variations in ρ due to the atomic structure only become visible at higher angles in the WAXS regime. This means that the total integrated intensity of the SAXS pattern (in 3D) is an invariant quantity proportional to the square Δρ2. In 1-dimensional projection, as usually recorded for an isotropic pattern this invariant quantity becomes 
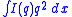, where the integral runs from q=0 to wherever the SAXS pattern is assumed to end and the WAXS pattern starts. It is also assumed that the density does not vary in the liquid or inside the particles, i.e. there is binary contrast.
In the transitional range at the high resolution end of the SAXS pattern the only contribution to the scattering come from the interface between the two phases and the intensity should drop with the fourth power of q if the interface is sharp. This is a consequence of the fact that in this regime any other structural features, e.g. interference between one surface of a particle and the one on the opposite side, are so random that they do not contribute. This is known as Porod's law (Günther Porod
, 1919-1984):
This allows the surface area S of the particles to be determined with SAXS. However, since the advent of fractal
mathematics it has become clear that this law requires adaptation because the value of the surface S may itself be a function of the yardstick by which it is measured. In the case of a fractally rough surface area with a dimensionality d between 2-3 Porod's law becomes:
Thus if plotted logarithmically the slope of ln(I) versus ln(q) would vary between -4 and -3 for such a surface fractal. Slopes less negative than -3 are also possible in fractal theory and they are described using a volume fractal model in which the whole system can be described to be self similar mathematically although not usually in reality in the nature.
in the latter case.
If the particles are dispersed in a solution and they are known to be monodisperse, all of the same size, then a typical strategy is to measure different concentration
s of particles in the solution. From the obtained SAXS patterns one can extrapolate to the intensity pattern one would get for a single particle. This is a necessary procedure that eliminates the concentration effect, which is a small shoulder that appears in the intensity patterns due to the proximity of neighbouring particles. The average distance between particles is then roughly the distance 2π/q*, where q* is the position of the shoulder on the scattering vector range q. The shoulder thus comes from the structure of the solution and this contribution is called the structure factor. One can write for the small-angle X-ray scattering intensity:
where
When the intensities from low concentrations of particles are extrapolated to infinite dilution, the structure factor is equal to 1 and no longer disturbs the determination of the particle shape from the form factor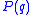
. One can then easily apply the Guinier approximation (also called Guinier law, André Guinier
1911-2000), which applies only at the very beginning of the scattering curve, at small q-values. According to the Guinier approximation the intensity at small q depends on the radius of gyration
of the particle.
An important part of the particle shape determination is usually the distance distribution function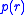
, which may be calculated from the intensity using a Fourier transform
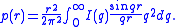
The distance distribution function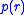
is related to the frequency of certain distances 
within the particle. Therefore it goes to zero at the largest diameter of the particle. It starts from zero at 
due to the multiplication by 
. The shape of the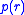 
-function already tells something about the shape of the particle. If the function is very symmetric, the particle is also highly symmetric, like a sphere. The distance distribution function should not be confused with the size distribution.
The particle shape analysis is especially popular in biological small-angle X-ray scattering, where one determines the shapes of protein
s and other natural colloidal polymers.
Small-angle scattering
Small-angle scattering is a scattering technique based on the deflection of a beam of particles, or an electromagnetic or acoustic wave, away from the straight trajectory after it interacts with structures that are much larger than the wavelength of the radiation. The deflection is small hence...
(SAS) technique where the elastic
Elastic collision
An elastic collision is an encounter between two bodies in which the total kinetic energy of the two bodies after the encounter is equal to their total kinetic energy before the encounter...
scattering of X-ray
X-ray
X-radiation is a form of electromagnetic radiation. X-rays have a wavelength in the range of 0.01 to 10 nanometers, corresponding to frequencies in the range 30 petahertz to 30 exahertz and energies in the range 120 eV to 120 keV. They are shorter in wavelength than UV rays and longer than gamma...
s (wavelength 0.1 ... 0.2 nm
Nanometre
A nanometre is a unit of length in the metric system, equal to one billionth of a metre. The name combines the SI prefix nano- with the parent unit name metre .The nanometre is often used to express dimensions on the atomic scale: the diameter...
) by a sample which has inhomogeneities in the nm-range, is recorded at very low angles (typically 0.1 - 10°). This angular range contains information about the shape and size of macromolecule
Macromolecule
A macromolecule is a very large molecule commonly created by some form of polymerization. In biochemistry, the term is applied to the four conventional biopolymers , as well as non-polymeric molecules with large molecular mass such as macrocycles...
s, characteristic distances of partially ordered materials, pore sizes, and other data. SAXS is capable of delivering structural information of macromolecules between 5 and 25 nm, of repeat distances in partially ordered systems of up to 150 nm. USAXS (ultra-small angle X-ray scattering) can resolve even larger dimensions.
SAXS and USAXS belong to a family of X-ray scattering techniques
X-ray scattering techniques
X-ray scattering techniques are a family of non-destructive analytical techniques which reveal information about the crystallographic structure, chemical composition, and physical properties of materials and thin films...
that are used in the characterization of materials. In the case of biologic macromolecule
Macromolecule
A macromolecule is a very large molecule commonly created by some form of polymerization. In biochemistry, the term is applied to the four conventional biopolymers , as well as non-polymeric molecules with large molecular mass such as macrocycles...
s such as protein
Protein
Proteins are biochemical compounds consisting of one or more polypeptides typically folded into a globular or fibrous form, facilitating a biological function. A polypeptide is a single linear polymer chain of amino acids bonded together by peptide bonds between the carboxyl and amino groups of...
s, the advantage of SAXS over crystallography
Crystallography
Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...
is that a crystalline sample is not needed. NMR
NMR spectroscopy
Nuclear magnetic resonance spectroscopy, most commonly known as NMR spectroscopy, is a research technique that exploits the magnetic properties of certain atomic nuclei to determine physical and chemical properties of atoms or the molecules in which they are contained...
methods encounter problems with macromolecules of higher molecular mass (> 30000-40000). However, owing to the random orientation of dissolved or partially ordered molecules, the spatial averaging leads to a loss of information in SAXS compared to crystallography.
Applications
SAXS is used for the determination of the microscale or nanoscale structure of particle systems in terms of such parameters as averaged particle sizes, shapes, distribution, and surface-to-volume ratio. The materials can be solid or liquid and they can contain solid, liquid or gaseous domains (so-called particles) of the same or another material in any combination. Not only particles, but also the structure of ordered systems like lamellae, and fractalFractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
-like materials can be studied. The method is accurate, non-destructive and usually requires only a minimum of sample preparation. Applications are very broad and include colloid
Colloid
A colloid is a substance microscopically dispersed evenly throughout another substance.A colloidal system consists of two separate phases: a dispersed phase and a continuous phase . A colloidal system may be solid, liquid, or gaseous.Many familiar substances are colloids, as shown in the chart below...
s of all types, metals, cement, oil, polymer
Polymer
A polymer is a large molecule composed of repeating structural units. These subunits are typically connected by covalent chemical bonds...
s, plastics, proteins, foods and pharmaceuticals can be found in research as well as in quality control. The X-ray
X-ray
X-radiation is a form of electromagnetic radiation. X-rays have a wavelength in the range of 0.01 to 10 nanometers, corresponding to frequencies in the range 30 petahertz to 30 exahertz and energies in the range 120 eV to 120 keV. They are shorter in wavelength than UV rays and longer than gamma...
source can be a laboratory source or synchrotron light
Synchrotron light
A synchrotron light source is a source of electromagnetic radiation produced by a synchrotron, which is artificially produced for scientific and technical purposes by specialized particle accelerators, typically accelerating electrons...
which provides a higher X-ray flux
Flux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
.
SAXS instruments
In a SAXS instrument a monochromatic beamLight beam
A light beam or beam of light is a narrow projection of light energy radiating from a source into a beam. Sunlight is a natural example of a light beam when filtered through various mediums...
of X-rays is brought to a sample from which some of the X-rays scatter, while most simply go through the sample without interacting with it. The scattered X-rays form a scattering pattern which is then detected at a detector which is typically a 2-dimensional flat X-ray detector situated behind the sample perpendicular to the direction of the primary beam that initially hit the sample. The scattering pattern contains the information on the structure of the sample.
The major problem that must be overcome in SAXS instrumentation is the separation of the weak scattered intensity from the strong main beam. The smaller the desired angle, the more difficult this becomes. The problem is comparable to one encountered when trying to observe a weakly radiant object close to the sun, like the sun's corona. Only if the moon blocks out the main light source does the corona become visible. Likewise, in SAXS the non-scattered beam that merely travels through the sample must be blocked, without blocking the closely adjacent scattered radiation. Most available X-ray sources produce divergent
Beam divergence
The beam divergence of an electromagnetic beam is an angular measure of the increase in beam diameter or radius with distance from the optical aperture or antenna aperture from which the electromagnetic beam emerges. The term is relevant only in the "far field", away from any focus of the beam...
beams and this compounds the problem. In principle the problem could be overcome by focusing
Focus (optics)
In geometrical optics, a focus, also called an image point, is the point where light rays originating from a point on the object converge. Although the focus is conceptually a point, physically the focus has a spatial extent, called the blur circle. This non-ideal focusing may be caused by...
the beam, but this is not easy when dealing with X-rays and was previously not done except on synchrotron
Synchrotron
A synchrotron is a particular type of cyclic particle accelerator in which the magnetic field and the electric field are carefully synchronised with the travelling particle beam. The proton synchrotron was originally conceived by Sir Marcus Oliphant...
s where large bent mirrors can be used. This is why most laboratory small angle devices rely on collimation
Collimated light
Collimated light is light whose rays are parallel, and therefore will spread slowly as it propagates. The word is related to "collinear" and implies light that does not disperse with distance , or that will disperse minimally...
instead.
Laboratory SAXS instruments can be divided into two main groups: point-collimation and line-collimation instruments:
- Point-collimation instruments have pinholePinholePinhole may refer to:* Pinhole , a rock band from Liverpool, England, later to become The Dead 60s* Pinhole , a song by Japanese rock band Ogre You Asshole* Pinhole camera, a camera that uses a pinhole to form an image instead of a lens...
s that shape the X-rayX-rayX-radiation is a form of electromagnetic radiation. X-rays have a wavelength in the range of 0.01 to 10 nanometers, corresponding to frequencies in the range 30 petahertz to 30 exahertz and energies in the range 120 eV to 120 keV. They are shorter in wavelength than UV rays and longer than gamma...
beam to a small circular or elliptical spot that illuminates the sample. Thus the scattering is centro-symmetrically distributed around the primary X-rayX-rayX-radiation is a form of electromagnetic radiation. X-rays have a wavelength in the range of 0.01 to 10 nanometers, corresponding to frequencies in the range 30 petahertz to 30 exahertz and energies in the range 120 eV to 120 keV. They are shorter in wavelength than UV rays and longer than gamma...
beam and the scattering pattern in the detection plane consists of circles around the primary beam. Owing to the small illuminated sample volume and the wastefulness of the collimation process — only those photons are allowed to pass that happen to fly in the right direction — the scattered intensity is small and therefore the measurement time is in the order of hours or days in case of very weak scatterers. If focusing optics like bent mirrors or bent monochromatorMonochromatorA monochromator is an optical device that transmits a mechanically selectable narrow band of wavelengths of light or other radiation chosen from a wider range of wavelengths available at the input...
crystals or collimating and monochromating optics like multilayers are used, measurement time can be greatly reduced. Point-collimation allows the orientation of non-isotropic systems (fibres, shearedShearing (physics)Shearing in continuum mechanics refers to the occurrence of a shear strain, which is a deformation of a material substance in which parallel internal surfaces slide past one another. It is induced by a shear stress in the material...
liquids) to be determined. - Line-collimation instruments confine the beam only in one dimension so that the beam profile is a long but narrow line. The illuminated sample volume is much larger compared to point-collimation and the scattered intensity at the same flux density is proportionally larger. Thus measuring times with line-collimation SAXS instruments are much shorter compared to point-collimation and are in the range of minutes. A disadvantage is that the recorded pattern is essentially an integrated superposition (a self-convolutionConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
) of many pinhole adjacent pinhole patterns. The resulting smearing can be easily removed using model-free algorithms or deconvolution methods based on Fourier transformation, but only if the system is isotropic. Line collimation is of great benefit for any isotropic nanostructured materials, e.g. proteins, surfactants, particle dispersion and emulsions.
Porod's law
SAXS patterns are typically represented as scattered intensity as a function of the magnitude of the scattering vector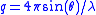. Here 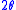is the angle between the incident X-ray beam and the detector measuring the scattered intensity, and is the wavelength of the X-rays. One interpretation of the scattering vector is that it is the resolution or yardstick with which the sample is observed. In the case of a two-phase sample, e.g. small particles in liquid suspension, the only contrast leading to scattering in the typical range of resolution of the SAXS is simply Δρ, the difference in average electron density between the particle and the surrounding liquid, because variations in ρ due to the atomic structure only become visible at higher angles in the WAXS regime. This means that the total integrated intensity of the SAXS pattern (in 3D) is an invariant quantity proportional to the square Δρ2. In 1-dimensional projection, as usually recorded for an isotropic pattern this invariant quantity becomes 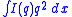, where the integral runs from q=0 to wherever the SAXS pattern is assumed to end and the WAXS pattern starts. It is also assumed that the density does not vary in the liquid or inside the particles, i.e. there is binary contrast.In the transitional range at the high resolution end of the SAXS pattern the only contribution to the scattering come from the interface between the two phases and the intensity should drop with the fourth power of q if the interface is sharp. This is a consequence of the fact that in this regime any other structural features, e.g. interference between one surface of a particle and the one on the opposite side, are so random that they do not contribute. This is known as Porod's law (Günther Porod
Günther Porod
Günther Porod was an Austrian physicist. He is best known for his work on the small-angle X-ray scattering method, done in collaboration with his teacher Otto Kratky...
, 1919-1984):
This allows the surface area S of the particles to be determined with SAXS. However, since the advent of fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
mathematics it has become clear that this law requires adaptation because the value of the surface S may itself be a function of the yardstick by which it is measured. In the case of a fractally rough surface area with a dimensionality d between 2-3 Porod's law becomes:
Thus if plotted logarithmically the slope of ln(I) versus ln(q) would vary between -4 and -3 for such a surface fractal. Slopes less negative than -3 are also possible in fractal theory and they are described using a volume fractal model in which the whole system can be described to be self similar mathematically although not usually in reality in the nature.
Scattering from particles
Small-angle scattering from particles can be used to determine the particle shape or their size distribution. A small-angle scattering pattern can be fitted with intensities calculated from different model shapes when the size distribution is known. If the shape is known, a size distribution may be fitted to the intensity. Typically one assumes the particles to be sphericalSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
in the latter case.
If the particles are dispersed in a solution and they are known to be monodisperse, all of the same size, then a typical strategy is to measure different concentration
Concentration
In chemistry, concentration is defined as the abundance of a constituent divided by the total volume of a mixture. Four types can be distinguished: mass concentration, molar concentration, number concentration, and volume concentration...
s of particles in the solution. From the obtained SAXS patterns one can extrapolate to the intensity pattern one would get for a single particle. This is a necessary procedure that eliminates the concentration effect, which is a small shoulder that appears in the intensity patterns due to the proximity of neighbouring particles. The average distance between particles is then roughly the distance 2π/q*, where q* is the position of the shoulder on the scattering vector range q. The shoulder thus comes from the structure of the solution and this contribution is called the structure factor. One can write for the small-angle X-ray scattering intensity:
where
is the intensity as a function of the magnitude 
of the scattering vector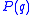
is the form factorAtomic form factorIn physics, the atomic form factor, or atomic scattering factor, is a measure of the scattering amplitude of a wave by an isolated atom. The atomic form factor depends on the type of scattering, which in turn depends on the nature of the incident radiation, typically X-ray, electron or neutron...- and
is the structure factorStructure factorIn condensed matter physics and crystallography, the static structure factor is a mathematical description of how a material scatters incident radiation...
.
When the intensities from low concentrations of particles are extrapolated to infinite dilution, the structure factor is equal to 1 and no longer disturbs the determination of the particle shape from the form factor
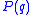. One can then easily apply the Guinier approximation (also called Guinier law, André GuinierAndré Guinier
André Guinier was a French physicist who did important work in the field of X-ray diffraction and solid-state physics. He worked at the Conservatoire National des Arts et Métiers, then taught at the University of Paris and later at the University of Paris-Sud in Orsay...
1911-2000), which applies only at the very beginning of the scattering curve, at small q-values. According to the Guinier approximation the intensity at small q depends on the radius of gyration
Radius of gyration
Radius of gyration or gyradius is the name of several related measures of the size of an object, a surface, or an ensemble of points. It is calculated as the root mean square distance of the objects' parts from either its center of gravity or an axis....
of the particle.
An important part of the particle shape determination is usually the distance distribution function
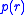, which may be calculated from the intensity using a Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
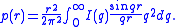
The distance distribution function
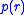is related to the frequency of certain distances within the particle. Therefore it goes to zero at the largest diameter of the particle. It starts from zero at due to the multiplication by . The shape of the 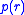-function already tells something about the shape of the particle. If the function is very symmetric, the particle is also highly symmetric, like a sphere. The distance distribution function should not be confused with the size distribution.The particle shape analysis is especially popular in biological small-angle X-ray scattering, where one determines the shapes of protein
Protein
Proteins are biochemical compounds consisting of one or more polypeptides typically folded into a globular or fibrous form, facilitating a biological function. A polypeptide is a single linear polymer chain of amino acids bonded together by peptide bonds between the carboxyl and amino groups of...
s and other natural colloidal polymers.
See also
- Biological Small angle X-ray scattering (SAXS)
- X-ray scattering techniquesX-ray scattering techniquesX-ray scattering techniques are a family of non-destructive analytical techniques which reveal information about the crystallographic structure, chemical composition, and physical properties of materials and thin films...
(SAXS instrumentation manufacturers) - GISAXS (Grazing-Incidence Small-Angle X-ray Scattering)
External links
- SAXS at a Synchrotron
- A movie explaining the workings of a pinhole collimated SAXS apparatus
- A movie explaining the workings of a slit collimated SAXS apparatus
- A movie demonstrating small-angle scattering using laserlight on a hair
- Small-angle scattering special interest group at the Advanced Photon Source, Argonne National Laboratory, USA
List of SAXS beamlines
- SAXS/D, SSRL Beamline 4-2, SLAC
USA - SAXS/WAXS/GISAXS Beamline, Advanced Light Source 7.3.3, LBNL USA
- SAXS endstation at the SIBYLS Beamline, Advanced Light Source 12.3.1 USA
- D11A beamline at Brazilian Synchrotron Light Laboratory
Brazil - ID02 SAXS/WAXS/USAXS beamline
Grenoble, France - SWING Beamline at Synchrotron SOLEIL Saint-Aubin, France
- Anomalous small-angle x-ray scattering (ASAXS)
Hamburg, Germany - BW4 Beamline at Desy Hamburg, Germany
- BL9 beamline of DELTA, Technical University of Dortmund Germany
- SAXS Beamline at Elettra
Trieste, Italy - cSAXS beamline, Swiss Light Source
Villigen, Switzerland - I22 beamline at Diamond Light Source, Harwell Science & Innovation Campus England, UK
- APS USAXS instrument, Advanced Photon Source, Argonne National Laboratory USA
- BNL SAXS X9 beamline, National Synchrotron Light Source, Brookhaven National Laboratory USA
SAXS Instrument Manufacturers
- Hecus X-Ray Systems Graz, Austria
- PANalyticalPANalyticalPANalytical is an international scientific instrumentation supplier which develops and manufactures X-ray diffraction and X-ray fluorescence equipment for use in research and industry. PANalytical was formerly Philips Analytical, a division of Philips, prior to its sale in 2002...
. The Netherlands - Anton Paar GmbH, Austria
- Bruker AXS, Germany
- RigakuRigakuRigaku Corporation is an international manufacturer and distributor of scientific, analytical and industrial instrumentation specializing in X-ray related technologies, including X-ray crystallography, X-ray diffraction , X-ray reflectivity, X-ray fluorescence , automation, cryogenics and X-ray...
Corporation, Japan - Xenocs, France