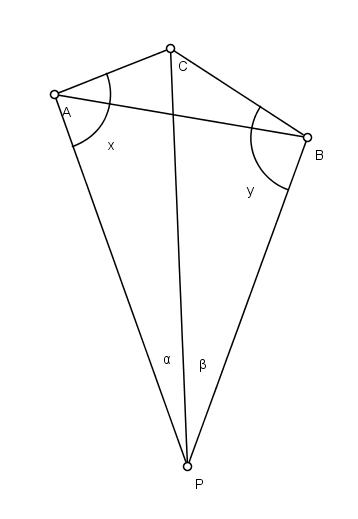
The Snellius–Pothenot problem is a problem in planar surveying

Surveying

See Also: Public Land Survey SystemSurveying or land surveying is the technique, profession, and science of accurately determining the terrestrial or three-dimensional position of points and the distances and angles between them...

. Given three known points A, B and C an observer at an unknown point P observes that the segment AC subtends an angle and the segment CB subtends an angle 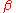; the problem is to determine the position of the point P. (See figure; the point denoted C is between A and B as seen from P).

Since it involves the observation of known points from an unknown point, the problem is an example of resection

Resection (orientation)

Resection is a method for determining a position using a compass and topographic map .-Resection versus intersection:...

. Historically it was first studied by Snellius

Willebrord Snellius

Willebrord Snellius was a Dutch astronomer and mathematician. In the west, especially the English speaking countries, his name has been attached to the law of refraction of light for several centuries, but it is now known that this law was first discovered by Ibn Sahl in 984...

, who found a solution around 1615.

Formulating the equations

First equation

Denoting the (unknown) angles CAP as x and CBP as y we get:


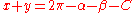
by using the sum of the angles formula for the quadrilateral

Quadrilateral

In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...

 PACB. The variable C represents the (known) internal angle in this quadrilateral at point C. (Note that in the case where the points C and P are on the same side of the line AB, the angle C will be greater than ).

Second equation

Applying the law of sines

Law of sines

In trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...

 in triangles PAC and PBC we can express PC in two different ways:


A useful trick at this point is to define an auxiliary angle such that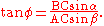


(A minor note: we should be concerned about division by zero, but consider that the problem is symmetric, so if one of the two given angles is zero we can, if needed, rename that angle alpha and call the other (non-zero) angle beta, reversing the roles of A and B as well. This will suffice to guarantee that the ratio above is well defined. An alternative approach to the zero angle problem is given in the algorithm below.)

With this substitution the equation becomes


We can use two known trigonometric identities, namely
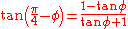and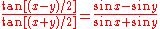


to put this in the form of the second equation we need:


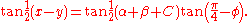
We now need to solve these two equations in two unknowns. Once x and y are known the various triangles can be solved straightforwardly to determine the position of P. The detailed procedure is shown below.

Solution algorithm

We are given two lengths AC and BC, and three angles , 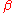and C. The solution proceeds as follows:

• calculate 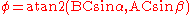. Where atan2
  Atan2
  In trigonometry, the two-argument function atan2 is a variation of the arctangent function. For any real arguments and not both equal to zero, is the angle in radians between the positive -axis of a plane and the point given by the coordinates on it...
  
   is a computer function, also called the arctangent of two arguments, that returns the arctangent of the ratio of the two values given. Note that in Microsoft Excel
  Microsoft Excel
  Microsoft Excel is a proprietary commercial spreadsheet application written and distributed by Microsoft for Microsoft Windows and Mac OS X. It features calculation, graphing tools, pivot tables, and a macro programming language called Visual Basic for Applications...
  
   the two arguments are reversed, so the proper syntax in Excel would be '=atan2(AC*sin(beta), BC*sin(alpha))'. The atan2 function correctly handles the case where one of the two arguments is zero.

• calculate

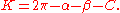
• calculate

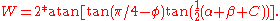
• find and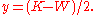

• if calculate 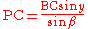else use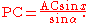

• find 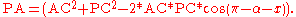(This comes from the law of cosines
  Law of cosines
  In trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...
  
  .)

• find

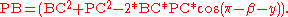
If we know the coordinates of A: x_A,y_A and C: x_C,y_C in some appropriate coordinate system then we can find the coordinates of P as well.

Geometric (graphical) solution

By the inscribed angle theorem the locus of points from which AC subtends an angle is a circle having its center on the midline of AC; from the center O of this circle AC subtends an angle . Similarly the locus of points from which CB subtends an angle 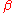is another circle. The desired point P is at the intersection of these two loci.

Therefore on a map or nautical chart showing the points A, B, C, the following graphical construction can be used:

• Draw the segment AC, the mid-point M and the midline, which crosses AC perpendicularly at M. On this line find the point O such that 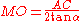. Draw the circle with center at O passing through A and C.

• Repeat the same construction with points B, C and the angle .

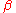• Mark P at the intersection of the two circles (the two circles intersect at two points; one intersection point is C and the other is the desired point P.)

This method of solution is sometimes called Cassini's method.

The indeterminate case

When the point P happens to be located on the same circle as A, B and C, the problem has an infinite number of solutions; the reason is that from any other point P' located on the arc APB of this circle the observer sees the same angles alpha and beta as from P (inscribed angle theorem). Thus the solution in this case is not uniquely determined.

The circle through ABC is known as the "danger circle", and observations made on (or very close to) this circle should be avoided. It is helpful to plot this circle on a map before making the observations.

A theorem on cyclic quadrilateral

Cyclic quadrilateral

In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...

s is helpful in detecting the indeterminate situation. The quadrilateral APBC is cyclic iff a pair of opposite angles (such as the angle at P and the angle at C) are supplementary i.e. iff 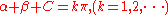. If this condition is observed the calculations should be stopped and an error message ("indeterminate case") returned.

Solved examples

(Adapted form Bowser, exercise 140, page 203). A, B and C are three objects such that AC = 435 (yard

Yard

A yard is a unit of length in several different systems including English units, Imperial units and United States customary units. It is equal to 3 feet or 36 inches...

s), CB = 320, and C = 255.8 degrees. From a station P it is observed that APC = 30 degrees and CPB = 15 degrees. Find the distances of P from A, B and C. (Note that in this case the points C and P are on the same side of the line AB, a different configuration from the one shown in the figure).

Answer: PA = 790, PB = 777, PC = 502.

A slightly more challenging test case for a computer program uses the same data but this time with CPB = 0. The program should, without blowing up, return the answers 843, 1157 and 837.

Naming controversy

The British authority on geodesy, George Tyrrell McCaw (1870-1942) wrote that the proper term in English was Snellius problem, while Snellius-Pothenot was the continental European usage.

McCaw thought the name of Laurent Pothenot (1650-1732) did not deserve to be included as he had made no original contribution, but merely restated Snellius 75 years later.