Spectral clustering
Encyclopedia
Given a set of data points A, the similarity matrix
may be defined as a matrix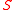
where 
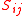represents a measure of the similarity between points 
. Spectral clustering techniques make use of the spectrum
of the similarity matrix of the data to perform dimensionality reduction
for clustering in fewer dimensions.
One such technique is the Normalized Cuts algorithm or Shi–Malik algorithm introduced by Jianbo Shi and Jitendra Malik, commonly used for image segmentation
. It partitions points into two sets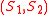
based on the eigenvector 
corresponding to the second-smallest eigenvalue of the Laplacian matrix
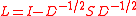
of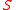
, where 
is the diagonal matrix
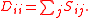
This partitioning may be done in various ways, such as by taking the median
of the components in 
, and placing all points whose component in 
is greater than 
in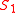 
, and the rest in 
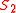. The algorithm can be used for hierarchical clustering by repeatedly partitioning the subsets in this fashion.
A related algorithm is the Meila–Shi algorithm, which takes the eigenvectors corresponding to the k largest eigenvalues of the matrix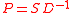
for some k, and then invokes another algorithm (e.g. k-means) to cluster points by their respective k components in these eigenvectors.
Similarity matrix
A similarity matrix is a matrix of scores which express the similarity between two data points. Similarity matrices are strongly related to their counterparts, distance matrices and substitution matrices.-Use in sequence alignment:...
may be defined as a matrix
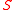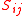where represents a measure of the similarity between points . Spectral clustering techniques make use of the spectrumSpectrum of a matrix
In mathematics, the spectrum of a matrix is the set of its eigenvalues. This notion can be extended to the spectrum of an operator in the infinite-dimensional case.The determinant equals the product of the eigenvalues...
of the similarity matrix of the data to perform dimensionality reduction
Dimensionality reduction
In machine learning, dimension reduction is the process of reducing the number of random variables under consideration, and can be divided into feature selection and feature extraction.-Feature selection:...
for clustering in fewer dimensions.
One such technique is the Normalized Cuts algorithm or Shi–Malik algorithm introduced by Jianbo Shi and Jitendra Malik, commonly used for image segmentation
Segmentation (image processing)
In computer vision, segmentation refers to the process of partitioning a digital image into multiple segments . The goal of segmentation is to simplify and/or change the representation of an image into something that is more meaningful and easier to analyze...
. It partitions points into two sets
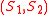based on the eigenvector corresponding to the second-smallest eigenvalue of the Laplacian matrixLaplacian matrix
In the mathematical field of graph theory the Laplacian matrix, sometimes called admittance matrix or Kirchhoff matrix, is a matrix representation of a graph. Together with Kirchhoff's theorem it can be used to calculate the number of spanning trees for a given graph. The Laplacian matrix can be...
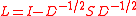
of
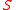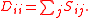
, where is the diagonal matrixThis partitioning may be done in various ways, such as by taking the median
of the components in , and placing all points whose component in is greater than in 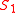, and the rest in 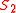. The algorithm can be used for hierarchical clustering by repeatedly partitioning the subsets in this fashion.A related algorithm is the Meila–Shi algorithm, which takes the eigenvectors corresponding to the k largest eigenvalues of the matrix
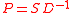for some k, and then invokes another algorithm (e.g. k-means) to cluster points by their respective k components in these eigenvectors.