Spectral risk measure
Encyclopedia
A Spectral risk measure is a risk measure
given as a weighted average of outcomes where bad outcomes are, typically, included with larger weights. A spectral risk measure is a function of portfolio
returns and outputs the amount of the numeraire
(typically a currency
) to be kept in reserve. A spectral risk measure is always a coherent risk measure
, but the converse does not always hold. An advantage of spectral measures is the way in which they can be related to risk aversion
, and particularly to a utility function, through the weights given to the possible portfolio returns.
Then a spectral risk measure 
where 
is non-negative, non-increasing, right-continuous, integrable function defined on 
such that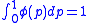 
is defined by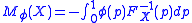
where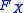
is the cumulative distribution function
for X.
If there are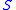
equiprobable outcomes with the corresponding payoffs given by the order statistics 
. Let 
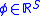. The measure
defined by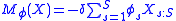 
is a spectral measure of risk if 
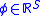satisfies the conditions
. Every spectral risk measure
satisfies:
Risk measure
A Risk measure is used to determine the amount of an asset or set of assets to be kept in reserve. The purpose of this reserve is to make the risks taken by financial institutions, such as banks and insurance companies, acceptable to the regulator...
given as a weighted average of outcomes where bad outcomes are, typically, included with larger weights. A spectral risk measure is a function of portfolio
Portfolio (finance)
Portfolio is a financial term denoting a collection of investments held by an investment company, hedge fund, financial institution or individual.-Definition:The term portfolio refers to any collection of financial assets such as stocks, bonds and cash...
returns and outputs the amount of the numeraire
Numéraire
Numéraire is a basic standard by which values are measured. Acting as the numéraire is one of the functions of money, to serve as a unit of account: to measure the worth of different goods and services relative to one another, i.e. in same units...
(typically a currency
Currency
In economics, currency refers to a generally accepted medium of exchange. These are usually the coins and banknotes of a particular government, which comprise the physical aspects of a nation's money supply...
) to be kept in reserve. A spectral risk measure is always a coherent risk measure
Coherent risk measure
In the field of financial economics there are a number of ways that risk can be defined; to clarify the concept theoreticians have described a number of properties that a risk measure might or might not have...
, but the converse does not always hold. An advantage of spectral measures is the way in which they can be related to risk aversion
Risk aversion
Risk aversion is a concept in psychology, economics, and finance, based on the behavior of humans while exposed to uncertainty....
, and particularly to a utility function, through the weights given to the possible portfolio returns.
Definition
Consider a portfolioPortfolio (finance)
Portfolio is a financial term denoting a collection of investments held by an investment company, hedge fund, financial institution or individual.-Definition:The term portfolio refers to any collection of financial assets such as stocks, bonds and cash...
Then a spectral risk measure where is non-negative, non-increasing, right-continuous, integrable function defined on such that 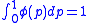is defined by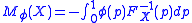where
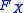is the cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
for X.
If there are
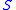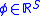equiprobable outcomes with the corresponding payoffs given by the order statistics . Let . The measure defined by 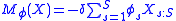is a spectral measure of risk if 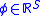satisfies the conditions- Nonnegativity:
for all 
, - Normalization:
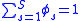, - Monotonicity :
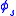is non-increasing, that is 
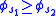if 
and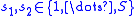 
.
Properties
Spectral risk measures are also coherentCoherent risk measure
In the field of financial economics there are a number of ways that risk can be defined; to clarify the concept theoreticians have described a number of properties that a risk measure might or might not have...
. Every spectral risk measure
satisfies:
- Positive Homogeneity: for every portfolio X and positive value
, 
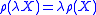; - Translation-Invariance: for every portfolio X and
, 
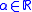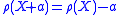; - Monotonicity: for all portfolios X and Y such that
, 
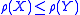; - Sub-additivity: for all portfolios X and Y,
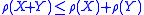; - Law-Invariance: for all portfolios X and Y with cumulative distribution functionCumulative distribution functionIn probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
s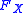
and 
respectively, if 
then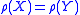 
; - Comonotonic Additivity: for every comonotonicComonotonicityIn probability theory, comonotonicity mainly refers to the perfect positive dependence between the components of a random vector, essentially saying that they can be represented as increasing functions of a single random variable...
random variables X and Y,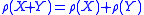
. Note that X and Y are comonotonic if for every 
.
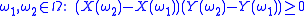Examples
- The expected shortfallExpected shortfallExpected shortfall is a risk measure, a concept used in finance to evaluate the market risk or credit risk of a portfolio. It is an alternative to value at risk that is more sensitive to the shape of the loss distribution in the tail of the distribution...
is a spectral measure of risk. - The expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
is trivially a spectral measure of risk.