
Comonotonicity
Encyclopedia
In probability theory
, comonotonicity mainly refers to the perfect positive dependence between the components of a random vector
, essentially saying that they can be represented as increasing functions of a single random variable. Perfect negative dependence is called countermonotonicity.
Comonotonicity is also related to the comonotonic additivity of the Choquet integral
.
The concept of comonotonicity has applications in financial risk management
and actuarial science
. In particular, the sum of the components X1 + X2 + ... + Xd is the riskiest if the joint probability distribution of the random vector (X1,X2,...,Xd) is comonotonic. Furthermore, the α-quantile
of the sum equals of the sum of the α-quantiles of its components, hence comonotonic random variables are quantile-additive.
For extensions of comonotonicity, see and .
This means that S is a totally ordered set.
on the d-dimensional Euclidean space
Rd and let F denote its multivariate cumulative distribution function
, that is
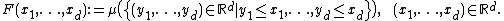
Furthermore, let F1,...,Fd denote the cumulative distribution functions of the d one-dimensional marginal distribution
s of μ, that means
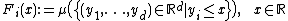
for every i ∈ {1,2,...,d}. Then μ is called comonotonic, if
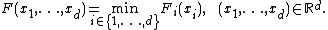
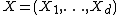 is called comonotonic, if its multivariate distribution
is called comonotonic, if its multivariate distribution
(the pushforward measure
) is comonotonic, this means
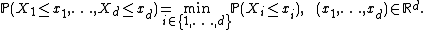
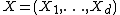 can be represented as
can be represented as
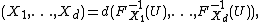
where =d stands for equality in distribution and U is a uniformly distributed random variable
on the unit interval
. It can be proved that a random vector is comonotonic if and only if all marginals are non-decreasing functions
(or all are non-increasing functions) of the same random variable.
 be an Rd-valued random vector. Then, for every i ∈ {1,2,...,d} and xi ∈ R,
be an Rd-valued random vector. Then, for every i ∈ {1,2,...,d} and xi ∈ R,

hence
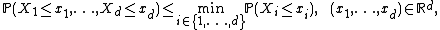
with equality everywhere if and only if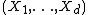 is comonotonic.
is comonotonic.
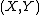 be a bivariate random vector such that the expected value
be a bivariate random vector such that the expected value
s of ,
,  and the product
and the product 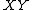 exist. Let
exist. Let 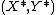 be a comonotonic bivariate random vector with the same one-dimensional marginal distributions as
be a comonotonic bivariate random vector with the same one-dimensional marginal distributions as  . Then it follows from Höffding's formula for the covariance and the Fréchet upper bound that
. Then it follows from Höffding's formula for the covariance and the Fréchet upper bound that
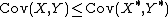
and, correspondingly,
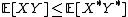
with equality if and only if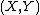 is comonotonic.
is comonotonic.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, comonotonicity mainly refers to the perfect positive dependence between the components of a random vector
Multivariate random variable
In mathematics, probability, and statistics, a multivariate random variable or random vector is a list of mathematical variables each of whose values is unknown, either because the value has not yet occurred or because there is imperfect knowledge of its value.More formally, a multivariate random...
, essentially saying that they can be represented as increasing functions of a single random variable. Perfect negative dependence is called countermonotonicity.
Comonotonicity is also related to the comonotonic additivity of the Choquet integral
Choquet integral
In decision theory, a Choquet integral is a way of measuring the expected utility of an uncertain event. It is applied specifically to membership functions and capacities. In imprecise probability theory, the Choquet integral is also used to calculate the lower expectation induced by a 2-monotone...
.
The concept of comonotonicity has applications in financial risk management
Financial risk management
Financial risk management is the practice of creating economic value in a firm by using financial instruments to manage exposure to risk, particularly credit risk and market risk. Other types include Foreign exchange, Shape, Volatility, Sector, Liquidity, Inflation risks, etc...
and actuarial science
Actuarial science
Actuarial science is the discipline that applies mathematical and statistical methods to assess risk in the insurance and finance industries. Actuaries are professionals who are qualified in this field through education and experience...
. In particular, the sum of the components X1 + X2 + ... + Xd is the riskiest if the joint probability distribution of the random vector (X1,X2,...,Xd) is comonotonic. Furthermore, the α-quantile
Quantile
Quantiles are points taken at regular intervals from the cumulative distribution function of a random variable. Dividing ordered data into q essentially equal-sized data subsets is the motivation for q-quantiles; the quantiles are the data values marking the boundaries between consecutive subsets...
of the sum equals of the sum of the α-quantiles of its components, hence comonotonic random variables are quantile-additive.
For extensions of comonotonicity, see and .
Comonotonicity of subsets of Rd
A subset S of Rd is called comonotonic if, for all (x1,x2,...,xd) and (y1,y2,...,yd) in S with xi < yi for some i ∈ {1,2,...,d}, it follows that xj ≤ yj for all j ∈ {1,2,...,d}.This means that S is a totally ordered set.
Comonotonicity of probability measures on Rd
Let μ be a probability measureProbability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
on the d-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rd and let F denote its multivariate cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
, that is
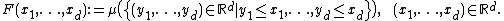
Furthermore, let F1,...,Fd denote the cumulative distribution functions of the d one-dimensional marginal distribution
Marginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained...
s of μ, that means
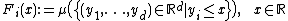
for every i ∈ {1,2,...,d}. Then μ is called comonotonic, if
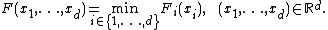
Comonotonicity of Rd-valued random vectors
An Rd-valued random vector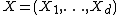 is called comonotonic, if its multivariate distribution
is called comonotonic, if its multivariate distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
(the pushforward measure
Pushforward measure
In measure theory, a pushforward measure is obtained by transferring a measure from one measurable space to another using a measurable function.-Definition:...
) is comonotonic, this means
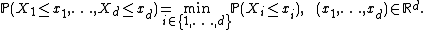
Properties
A comonotonic Rd-valued random vector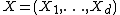 can be represented as
can be represented as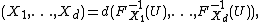
where =d stands for equality in distribution and U is a uniformly distributed random variable
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
on the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
. It can be proved that a random vector is comonotonic if and only if all marginals are non-decreasing functions
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
(or all are non-increasing functions) of the same random variable.
Fréchet upper bound for cumulative distribution functions
Let be an Rd-valued random vector. Then, for every i ∈ {1,2,...,d} and xi ∈ R,
be an Rd-valued random vector. Then, for every i ∈ {1,2,...,d} and xi ∈ R,
hence
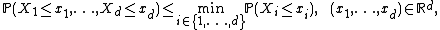
with equality everywhere if and only if
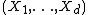 is comonotonic.
is comonotonic.Upper bound for the covariance
Let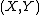 be a bivariate random vector such that the expected value
be a bivariate random vector such that the expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
s of
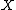 ,
, 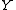 and the product
and the product 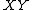 exist. Let
exist. Let 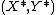 be a comonotonic bivariate random vector with the same one-dimensional marginal distributions as
be a comonotonic bivariate random vector with the same one-dimensional marginal distributions as  . Then it follows from Höffding's formula for the covariance and the Fréchet upper bound that
. Then it follows from Höffding's formula for the covariance and the Fréchet upper bound that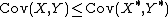
and, correspondingly,
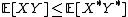
with equality if and only if
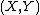 is comonotonic.
is comonotonic.

