
Choquet integral
Encyclopedia
In decision theory
, a Choquet integral is a way of measuring the expected utility of an uncertain event. It is applied specifically to membership functions
and capacities
. In imprecise probability theory
, the Choquet integral is also used to calculate the lower expectation induced by a 2-monotone lower probability
, or the upper expectation induced by a 2-alternating upper probability
. This integral was created by the French mathematician Gustave Choquet
.
Using the Choquet integral to denote the expected utility of belief functions measured with capacities is a way to reconcile the Ellsberg paradox
and the Allais paradox
.
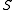 be a set, and let
be a set, and let 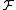 be any collection of subsets of
be any collection of subsets of 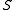 . Consider a function
. Consider a function 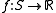 and a monotone set function
and a monotone set function
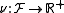 .
.
Assume that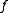 is measurable with respect to
is measurable with respect to  , that is
, that is
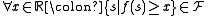
Then the Choquet integral of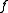 with respect to
with respect to  is defined by:
is defined by:

where the integrals on the right-hand side are the usual Riemann integral
(the integrands are integrable because they are monotone in ).
).
 is not a probability measure, it may hold that
is not a probability measure, it may hold that
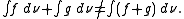
for some functions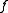 and
and 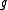 .
.
The Choquet integral does satisfy the following properties.
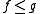 then
then
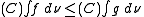
Positive homogeneity
For all 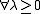 it holds that
it holds that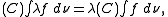
Comonotone additivity
If 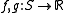 are comonotone functions, that is, if for all
are comonotone functions, that is, if for all 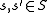 it holds that
it holds that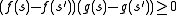 .
.
then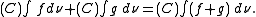
 is 2-alternating, then
is 2-alternating, then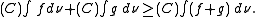
 is 2-monotone, then
is 2-monotone, then
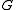 denote a cumulative distribution function
denote a cumulative distribution function
such that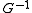 is
is  integrable. Then this following formula is often referred to as Choquet Integral:
integrable. Then this following formula is often referred to as Choquet Integral: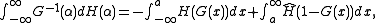
where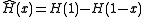 .
.
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
, a Choquet integral is a way of measuring the expected utility of an uncertain event. It is applied specifically to membership functions
Membership function (mathematics)
The membership function of a fuzzy set is a generalization of the indicator function in classical sets. In fuzzy logic, it represents the degree of truth as an extension of valuation. Degrees of truth are often confused with probabilities, although they are conceptually distinct, because fuzzy...
and capacities
Capacity of a set
In mathematics, the capacity of a set in Euclidean space is a measure of that set's "size". Unlike, say, Lebesgue measure, which measures a set's volume or physical extent, capacity is a mathematical analogue of a set's ability to hold electrical charge. More precisely, it is the capacitance of...
. In imprecise probability theory
Imprecise probability
Imprecise probability generalizes probability theory to allow for partial probability specifications, and is applicable when information is scarce, vague, or conflicting, in which case a unique probability distribution may be hard to identify...
, the Choquet integral is also used to calculate the lower expectation induced by a 2-monotone lower probability
Upper and lower probabilities
Upper and lower probabilities are representations of imprecise probability. Whereas probability theory uses a single number, the probability, to describe how likely an event is to occur, this method uses two numbers: the upper probability of the event and the lower probability of the event.Because...
, or the upper expectation induced by a 2-alternating upper probability
Upper and lower probabilities
Upper and lower probabilities are representations of imprecise probability. Whereas probability theory uses a single number, the probability, to describe how likely an event is to occur, this method uses two numbers: the upper probability of the event and the lower probability of the event.Because...
. This integral was created by the French mathematician Gustave Choquet
Gustave Choquet
Gustave Choquet was a French mathematician.Choquet was born in Solesmes, Nord. His contributions include work in functional analysis, potential theory, topology and measure theory...
.
Using the Choquet integral to denote the expected utility of belief functions measured with capacities is a way to reconcile the Ellsberg paradox
Ellsberg paradox
The Ellsberg paradox is a paradox in decision theory and experimental economics in which people's choices violate the expected utility hypothesis.An alternate viewpoint is that expected utility theory does not properly describe actual human choices...
and the Allais paradox
Allais paradox
The Allais paradox is a choice problem designed by Maurice Allais to show an inconsistency of actual observed choices with the predictions of expected utility theory.-Statement of the Problem:...
.
Definition
More specifically, let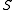 be a set, and let
be a set, and let 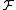 be any collection of subsets of
be any collection of subsets of 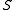 . Consider a function
. Consider a function 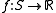 and a monotone set function
and a monotone set functionSet function
In mathematics, a set function is a function whose input is a set. The output is usually a number. Often the input is a set of real numbers, a set of points in Euclidean space, or a set of points in some measure space.- Examples :...
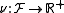 .
.Assume that
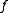 is measurable with respect to
is measurable with respect to  , that is
, that is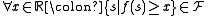
Then the Choquet integral of
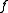 with respect to
with respect to  is defined by:
is defined by:
where the integrals on the right-hand side are the usual Riemann integral
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
(the integrands are integrable because they are monotone in
 ).
).Properties
In general the Choquet integral does not satisfy additivity. More specifically, if is not a probability measure, it may hold that
is not a probability measure, it may hold that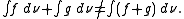
for some functions
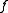 and
and 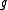 .
.The Choquet integral does satisfy the following properties.
Monotonicity
If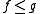 then
then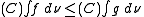
Positive homogeneityHomogeneous functionIn mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
For all 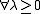 it holds that
it holds that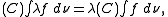
Comonotone additivityAdditive functionIn mathematics the term additive function has two different definitions, depending on the specific field of application.In algebra an additive function is a function that preserves the addition operation:for any two elements x and y in the domain. For example, any linear map is additive...
If 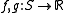 are comonotone functions, that is, if for all
are comonotone functions, that is, if for all 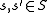 it holds that
it holds that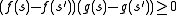 .
.then
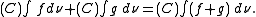
Subadditivity
If is 2-alternating, then
is 2-alternating, then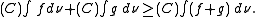
Superadditivity
If is 2-monotone, then
is 2-monotone, then
Alternative Representation
Let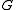 denote a cumulative distribution function
denote a cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
such that
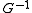 is
is  integrable. Then this following formula is often referred to as Choquet Integral:
integrable. Then this following formula is often referred to as Choquet Integral: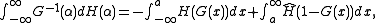
where
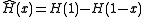 .
.
- choose
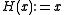 to get
to get 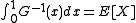 ,
, - choose
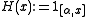 to get
to get 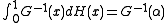
External links
- Gilboa I., Schmeidler D.David SchmeidlerDavid Schmeidler is an Israeli mathematician and economic theorist with important contributions in the theory of individual decision making under uncertainty . He currently holds professorships at Ohio State University and Tel Aviv University. He received his PhD in Mathematics from the Hebrew...
(1992), Additive Representations of Non-Additive Measures and the Choquet Integral, Discussion Paper n° 985...

