Imprecise probability
Encyclopedia
Imprecise probability generalizes probability theory
to allow for partial probability specifications, and is applicable when information is scarce, vague, or conflicting, in which case a unique probability distribution may be hard to identify. Thereby, the theory aims to represent the available knowledge more accurately.
distribution, usually satisfying Kolmogorov
's axioms (or a variation thereof), as argued by Laplace
, de Finetti
, Ramsey
, Cox
, Lindley
, and many others. However, this has not been unanimously accepted by scientists, statisticians, and probabilists: it has been argued that some modification or broadening of probability theory is required, because one may not always be able to provide a probability for every event, particularly when only little information or data is available—an early example of such criticism is Boole
's critique of Laplace
's work—, or when we wish to model probabilities that a group agrees with, rather than those of a single individual.
Perhaps the most straightforward generalization is to replace a single probability specification with an interval specification. Lower and upper probabilities
, denoted by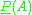
and 
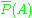, or more generally, lower and upper expectations (previsions), aim to fill this gap:
with a flexible continuum in between.
Some approaches, summarized under the name nonadditive probabilities, directly use one of these set function
s, assuming the other one to be naturally defined such that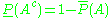
, with 
the complement of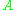 
. Other related concepts understand the corresponding intervals 
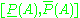for all events as the basic entity.
, who aimed to reconcile the theories of logic (which can express complete ignorance) and probability. In the 1920s, in A Treatise on Probability
, Keynes
formulated and applied an explicit interval estimate approach to probability.
Since the 1990s, the theory has gathered strong momentum, initiated by comprehensive foundations put forward by Walley, who coined the term imprecise probability, by Kuznetsov, and by Weichselberger, who uses the term interval probability. Walley's theory extends the traditional subjective probability theory via buying and selling prices for gambles, whereas Weichselberger's approach generalizes Kolmogorov
's axioms without imposing an interpretation.
Usually assumed consistency conditions relate imprecise probability assignments to non-empty closed convex sets of probability distributions. Therefore, as a welcome by-product, the theory also provides a formal framework for models used in robust statistics
and non-parametric statistics
. Included are also concepts based on Choquet integration
, and so-called two-monotone and totally monotone capacities, which have become very popular in artificial intelligence
under the name (Dempster-Shafer) belief functions. Moreover, there is a strong connection to Shafer and Vovk's notion of game-theoretic probability.
, including:
, Walley’s formulation of imprecise probabilities is based on the subjective variant of the Bayesian interpretation
of probability. Walley defines upper and lower probabilities as special cases of upper and lower previsions and the gambling framework advanced by Bruno de Finetti
. In simple terms, a decision maker’s lower prevision is the highest price at which the decision maker is sure he or she would buy a gamble, and the upper prevision is the lowest price at which the decision maker is sure he or she would buy the opposite of the gamble (which is equivalent to selling the original gamble). If the upper and lower previsions are equal, then they jointly represent the decision maker’s fair price for the gamble, the price at which the decision maker is willing to take either side of the gamble. The existence of a fair price leads to precise probabilities.
The allowance for imprecision, or a gap between a decision maker's upper and lower previsions, is the primary difference between precise and imprecise probability theories. Interestingly, such gaps arise naturally in betting markets
which happen to be financially illiquid due to asymmetric information. Also, imprecision is useful for dealing with expert elicitation
, because:
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
to allow for partial probability specifications, and is applicable when information is scarce, vague, or conflicting, in which case a unique probability distribution may be hard to identify. Thereby, the theory aims to represent the available knowledge more accurately.
Introduction
Quantification of uncertainty is often done using a probabilityProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
distribution, usually satisfying Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
's axioms (or a variation thereof), as argued by Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
, de Finetti
Bruno de Finetti
Bruno de Finetti was an Italian probabilist, statistician and actuary, noted for the "operational subjective" conception of probability...
, Ramsey
Frank P. Ramsey
Frank Plumpton Ramsey was a British mathematician who, in addition to mathematics, made significant and precocious contributions in philosophy and economics before his death at the age of 26...
, Cox
Cox's theorem
Cox's theorem, named after the physicist Richard Threlkeld Cox, is a derivation of the laws of probability theory from a certain set of postulates. This derivation justifies the so-called "logical" interpretation of probability. As the laws of probability derived by Cox's theorem are applicable to...
, Lindley
Dennis Lindley
Dennis Victor Lindley is a British statistician, decision theorist and leading advocate of Bayesian statistics.Dennis Lindley grew up in the south-west London suburb of Surbiton. He was an only child and his father was a local building contractor...
, and many others. However, this has not been unanimously accepted by scientists, statisticians, and probabilists: it has been argued that some modification or broadening of probability theory is required, because one may not always be able to provide a probability for every event, particularly when only little information or data is available—an early example of such criticism is Boole
George Boole
George Boole was an English mathematician and philosopher.As the inventor of Boolean logic—the basis of modern digital computer logic—Boole is regarded in hindsight as a founder of the field of computer science. Boole said,...
's critique of Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
's work—, or when we wish to model probabilities that a group agrees with, rather than those of a single individual.
Perhaps the most straightforward generalization is to replace a single probability specification with an interval specification. Lower and upper probabilities
Upper and lower probabilities
Upper and lower probabilities are representations of imprecise probability. Whereas probability theory uses a single number, the probability, to describe how likely an event is to occur, this method uses two numbers: the upper probability of the event and the lower probability of the event.Because...
, denoted by
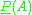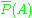and , or more generally, lower and upper expectations (previsions), aim to fill this gap:
- the special case with
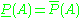for all events 
provides precise probability, whilst 
and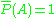 
represents no constraint at all on the specification of 
,
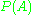with a flexible continuum in between.
Some approaches, summarized under the name nonadditive probabilities, directly use one of these set function
Set function
In mathematics, a set function is a function whose input is a set. The output is usually a number. Often the input is a set of real numbers, a set of points in Euclidean space, or a set of points in some measure space.- Examples :...
s, assuming the other one to be naturally defined such that
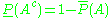, with the complement of 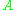. Other related concepts understand the corresponding intervals 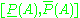for all events as the basic entity.History
The idea to use imprecise probability has a long history. The first formal treatment dates back at least to the middle of the nineteenth century, by George BooleGeorge Boole
George Boole was an English mathematician and philosopher.As the inventor of Boolean logic—the basis of modern digital computer logic—Boole is regarded in hindsight as a founder of the field of computer science. Boole said,...
, who aimed to reconcile the theories of logic (which can express complete ignorance) and probability. In the 1920s, in A Treatise on Probability
A Treatise on Probability
A Treatise on Probability was published by John Maynard Keynes while at Cambridge University in 1921. The Treatise attacked the classical theory of probability and proposed a "logical-relationist" theory instead...
, Keynes
John Maynard Keynes
John Maynard Keynes, Baron Keynes of Tilton, CB FBA , was a British economist whose ideas have profoundly affected the theory and practice of modern macroeconomics, as well as the economic policies of governments...
formulated and applied an explicit interval estimate approach to probability.
Since the 1990s, the theory has gathered strong momentum, initiated by comprehensive foundations put forward by Walley, who coined the term imprecise probability, by Kuznetsov, and by Weichselberger, who uses the term interval probability. Walley's theory extends the traditional subjective probability theory via buying and selling prices for gambles, whereas Weichselberger's approach generalizes Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
's axioms without imposing an interpretation.
Usually assumed consistency conditions relate imprecise probability assignments to non-empty closed convex sets of probability distributions. Therefore, as a welcome by-product, the theory also provides a formal framework for models used in robust statistics
Robust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
and non-parametric statistics
Non-parametric statistics
In statistics, the term non-parametric statistics has at least two different meanings:The first meaning of non-parametric covers techniques that do not rely on data belonging to any particular distribution. These include, among others:...
. Included are also concepts based on Choquet integration
Choquet integral
In decision theory, a Choquet integral is a way of measuring the expected utility of an uncertain event. It is applied specifically to membership functions and capacities. In imprecise probability theory, the Choquet integral is also used to calculate the lower expectation induced by a 2-monotone...
, and so-called two-monotone and totally monotone capacities, which have become very popular in artificial intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
under the name (Dempster-Shafer) belief functions. Moreover, there is a strong connection to Shafer and Vovk's notion of game-theoretic probability.
Mathematical models
So, the term imprecise probability—although an unfortunate misnomer as it enables more accurate quantification of uncertainty than precise probability—appears to have been established in the 1990s, and covers a wide range of extensions of the theory of probabilityProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, including:
- previsions
- lower and upper probabilities, or interval probabilitiesUpper and lower probabilitiesUpper and lower probabilities are representations of imprecise probability. Whereas probability theory uses a single number, the probability, to describe how likely an event is to occur, this method uses two numbers: the upper probability of the event and the lower probability of the event.Because...
- belief functions
- possibility and necessity measuresPossibility theoryPossibility theory is a mathematical theory for dealing with certain types of uncertainty and is an alternative to probability theory. Professor Lotfi Zadeh first introduced possibility theory in 1978 as an extension of his theory of fuzzy sets and fuzzy logic. D. Dubois and H. Prade further...
- lower and upper previsions
- comparative probability orderings
- partial preference orderings
- sets of desirable gambles
- p-boxesProbability boxA probability box is a characterization of an uncertain number consisting of both aleatoric and epistemic uncertainties that is often used in risk analysis or quantitative uncertainty modeling where numerical calculations must be performed...
- robust Bayes methodsRobust Bayes analysisRobust Bayes analysis, also called Bayesian sensitivity analysis, investigates the robustness of answers from a Bayesian analysis to uncertainty about the precise details of the analysis. An answer is robust if it does not depend sensitively on the assumptions and calculation inputs on which it is...
Interpretation of imprecise probabilities according to Walley
A unification of many of the above mentioned imprecise probability theories was proposed by Walley, although this is in no way the first attempt to formalize imprecise probabilities. In terms of probability interpretationsProbability interpretations
The word probability has been used in a variety of ways since it was first coined in relation to games of chance. Does probability measure the real, physical tendency of something to occur, or is it just a measure of how strongly one believes it will occur? In answering such questions, we...
, Walley’s formulation of imprecise probabilities is based on the subjective variant of the Bayesian interpretation
Bayesian probability
Bayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
of probability. Walley defines upper and lower probabilities as special cases of upper and lower previsions and the gambling framework advanced by Bruno de Finetti
Bruno de Finetti
Bruno de Finetti was an Italian probabilist, statistician and actuary, noted for the "operational subjective" conception of probability...
. In simple terms, a decision maker’s lower prevision is the highest price at which the decision maker is sure he or she would buy a gamble, and the upper prevision is the lowest price at which the decision maker is sure he or she would buy the opposite of the gamble (which is equivalent to selling the original gamble). If the upper and lower previsions are equal, then they jointly represent the decision maker’s fair price for the gamble, the price at which the decision maker is willing to take either side of the gamble. The existence of a fair price leads to precise probabilities.
The allowance for imprecision, or a gap between a decision maker's upper and lower previsions, is the primary difference between precise and imprecise probability theories. Interestingly, such gaps arise naturally in betting markets
Prediction market
Prediction markets are speculative markets created for the purpose of making predictions...
which happen to be financially illiquid due to asymmetric information. Also, imprecision is useful for dealing with expert elicitation
Expert elicitation
In science, engineering, and research, expert elicitation is the synthesis of opinions of experts of a subject where there is uncertainty due to insufficient data or when such data is unattainable because of physical constraints or lack of resources. Expert elicitation is essentially a scientific...
, because:
- People have a limited ability to determine their own subjective probabilities and might find that they can only provide an interval.
- As an interval is compatible with a range of opinions, the analysis ought to be more convincing to a range of different people.