Probability interpretations
Encyclopedia
The word probability
has been used in a variety of ways since it was first coined in relation to games of chance. Does probability measure the real, physical tendency of something to occur, or is it just a measure of how strongly one believes it will occur? In answering such questions, we interpret the probability values of probability theory
.
There are two broad categories of probability interpretations which can be called 'physical' and 'evidential' probabilities. Physical probabilities, which are also called objective or frequency probabilities
, are associated with random physical systems such as roulette wheels, rolling dice and radioactive atoms. In such systems, a given type of event (such as the dice yielding a six) tends to occur at a persistent rate, or 'relative frequency', in a long run of trials. Physical probabilities either explain, or are invoked to explain, these stable frequencies. Thus talk about physical probability makes sense only when dealing with well defined random
experiments. The two main kinds of theory of physical probability are frequentist
accounts (such as those of Venn, Reichenbach and von Mises) and propensity
accounts (such as those of Popper, Miller, Giere and Fetzer).
Evidential probability, also called Bayesian probability
(or subjectivist probability), can be assigned to any statement whatsoever, even when no random process is involved, as a way to represent its subjective plausibility, or the degree to which the statement is supported by the available evidence. On most accounts, evidential probabilities are considered to be degrees of belief, defined in terms of dispositions to gamble at certain odds. The four main evidential interpretations are the classical (e.g. Laplace's) interpretation, the subjective interpretation (de Finetti and Savage), the epistemic or inductive interpretation (Ramsey
, Cox) and the logical interpretation (Keynes and Carnap
).
Some interpretations of probability are associated with approaches to statistical inference
, including theories of estimation
and hypothesis testing
. The physical interpretation, for example, is taken by followers of "frequentist" statistical methods, such as R. A. Fisher
, Jerzy Neyman
and Egon Pearson
. Statisticians of the opposing Bayesian
school typically accept the existence and importance of physical probabilities, but also consider the calculation of evidential probabilities to be both valid and necessary in statistics. This article, however, focuses on the interpretations of probability rather than theories of statistical inference.
The terminology of this topic is rather confusing, in part because probabilities are studied within so many different academic fields. The word "frequentist" is especially tricky. To philosophers it refers to a particular theory of physical probability, one that has more or less been abandoned. To scientists, on the other hand, "frequentist probability
" is just what philosophers call physical (or objective) probability. Those who promote Bayesian inference view "frequentist statistics" as an approach to statistical inference that recognises only physical probabilities. Also the word "objective", as applied to probability, sometimes means exactly what "physical" means here, but is also used of evidential probabilities that are fixed by rational constraints, such as logical and epistemic probabilities.
concepts and ordinary language as it is used by non-mathematicians.
Probability theory
is an established field of study in mathematics. It has its origins in correspondence discussing the mathematics of games of chance between Blaise Pascal
and Pierre de Fermat
in the seventeenth century, and was formalized and rendered axiom
atic as a distinct branch of mathematics by Andrey Kolmogorov
in the twentieth century. In its axiomatic form, mathematical statements about probability theory carry the same sort of epistemological confidence shared by other mathematical statements in the philosophy of mathematics
.
The mathematical analysis originated in observations of the behaviour of game equipment such as playing card
s and dice
, which are designed specifically to introduce random and equalized elements; in mathematical terms, they are subjects of indifference
. This is not the only way probabilistic statements are used in ordinary human language: when people say that "it will probably rain", they typically do not mean that the outcome of rain versus not-rain is a random factor that the odds currently favor; instead, such statements are perhaps better understood as qualifying their expectation of rain with a degree of confidence. Likewise, when it is written that "the most probable explanation" of the name of Ludlow, Massachusetts
"is that it was named after Roger Ludlow
", what is meant here is not that Roger Ludlow is favored by a random factor, but rather that this is the most plausible explanation of the evidence, which admits other, less likely explanations.
Thomas Bayes
attempted to provide a logic
that could handle varying degrees of confidence; as such, Bayesian probability
is an attempt to recast the representation of probabilistic statements as an expression of the degree of confidence by which the beliefs they express are held.
Though probability initially may have had lowly motivations, its modern influence and use is widespread ranging from medicine, through practical pursuits
, all the way to the higher-order and the sublime
.
, is now known as the classical definition. Developed from studies of games of chance (such as rolling dice
) it states that probability is shared equally between all the possible outcomes, provided these outcomes can be deemed equally likely.
This can be represented mathematically as follows:
If a random experiment can result in N mutually exclusive and equally likely outcomes and if NA of these outcomes result in the occurrence of the event A, the probability of A is defined by
.
There are two clear limitations to the classical definition. Firstly, it is applicable only to situations in which there is only a 'finite' number of possible outcomes. But some important random experiments, such as tossing a coin
until it rises heads, give rise to an infinite set of outcomes. And secondly, you need to determine in advance that all the possible outcomes are equally likely without relying on the notion of probability to avoid circularity—for instance, by symmetry considerations.
Frequentists posit that the probability of an event is its relative frequency over time, i.e., its relative frequency of occurrence after repeating a process a large number of times under similar conditions. This is also known as aleatory
probability. The events are assumed to be governed by some random
physical phenomena, which are either phenomena that are predictable, in principle, with sufficient information (see Determinism
); or phenomena which are essentially unpredictable. Examples of the first kind include tossing dice
or spinning a roulette
wheel; an example of the second kind is radioactive decay
. In the case of tossing a fair coin, frequentists say that the probability of getting a heads is 1/2, not because there are two equally likely outcomes but because repeated series of large numbers of trials demonstrate that the empirical frequency converges to the limit 1/2 as the number of trials goes to infinity.
If we denote by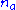
the number of occurrences of an event 
in 
trials, then if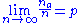 
we say that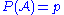 
The frequentist view has its own problems. It is of course impossible to actually perform an infinity of repetitions of a random experiment to determine the probability of an event. But if only a finite number of repetitions of the process are performed, different relative frequencies will appear in different series of trials. If these relative frequencies are to define the probability, the probability will be slightly different every time it is measured. But the real probability should be the same every time. If we acknowledge the fact that we only can measure a probability with some error of measurement attached, we still get into problems as the error of measurement can only be expressed as a probability, the very concept we are trying to define. This renders even the frequency definition circular.
The differences between these interpretations are rather small, and may seem inconsequential. One of the main points of disagreement lies in the relation between probability and belief. Logical probabilities are conceived to be objective, logical relations between propositions (or sentences), and hence not to depend in any way upon belief. They are degrees of (partial) entailment
, or degrees of logical consequence, not degrees of belief
. (They do, nevertheless, dictate proper degrees of belief, as is discussed below.) Frank P. Ramsey
, on the other hand, was skeptical about the existence of such objective logical relations and argued that (evidential) probability is "the logic of partial belief" ("Truth and Probability", 1926, p. 157). In other words, Ramsey held that epistemic probabilities simply are degrees of rational belief, rather than being logical relations that merely constrain degrees of rational belief.
Another point of disagreement concerns the uniqueness of evidential probability, relative to a given state of knowledge. Rudolf Carnap
held, for example, that logical principles always determine a unique logical probability for any statement, relative to any body of evidence. Ramsey, by contrast, thought that while degrees of belief are subject to some rational constraints (such as, but not limited to, the axioms of probability) these constraints usually do not determine a unique value. Rational people, in other words, may differ somewhat in their degrees of belief, even if they all have the same information.
Propensities, or chances, are not relative frequencies, but purported causes of the observed stable relative frequencies. Propensities are invoked to explain why repeating a certain kind of experiment will generate a given outcome type at a persistent rate, which are known as propensities or chances. Frequentists are unable to take this approach, since relative frequencies do not exist for single tosses of a coin, but only for large ensembles or collectives. In contrast, a propensitist is able to use the law of large numbers
to explain the behaviour of long-run frequencies. This law, which is a consequence of the axioms of probability, says that if (for example) a coin is tossed repeatedly many times, in such a way that its probability of landing heads is the same on each toss, and the outcomes are probabilistically independent, then the relative frequency of heads will (with high probability) be close to the probability of heads on each single toss. This law allows that stable long-run frequencies are a manifestation of invariant single-case probabilities. In addition to explaining the emergence of stable relative frequencies, the idea of propensity is motivated by the desire to make sense of single-case probability attributions in quantum mechanics, such as the probability of decay
of a particular atom
at a particular time.
The main challenge facing propensity theories is to say exactly what propensity means. (And then, of course, to show that propensity thus defined has the required properties.) At present, unfortunately, none of the well-recognised accounts of propensity comes close to meeting this challenge.
A propensity theory of probability was given by Charles Sanders Peirce. A later propensity theory was proposed by philosopher Karl Popper
, who had only slight acquaintance with the writings of C. S. Peirce, however. Popper noted that the outcome of a physical experiment is produced by a certain set of "generating conditions". When we repeat an experiment, as the saying goes, we really perform another experiment with a (more or less) similar set of generating conditions. To say that a set of generating conditions has propensity p of producing the outcome E means that those exact conditions, if repeated indefinitely, would produce an outcome sequence in which E occurred with limiting relative frequency p. For Popper then, a deterministic experiment would have propensity 0 or 1 for each outcome, since those generating conditions would have same outcome on each trial. In other words, non-trivial propensities (those that differ from 0 and 1) only exist for genuinely indeterministic experiments.
A number of other philosophers, including David Miller
and Donald A. Gillies
, have proposed propensity theories somewhat similar to Popper's.
Other propensity theorists (e.g. Ronald Giere) do not explicitly define propensities at all, but rather see propensity as defined by the theoretical role it plays in science. They argue, for example, that physical magnitudes such as electrical charge cannot be explicitly defined either, in terms of more basic things, but only in terms of what they do (such as attracting and repelling other electrical charges). In a similar way, propensity is whatever fills the various roles that physical probability plays in science.
What roles does physical probability play in science? What are its properties? One central property of chance is that, when known, it constrains rational belief to take the same numerical value. David Lewis called this the Principal Principle, a term that philosophers have mostly adopted. For example, suppose you are certain that a particular biased coin has propensity 0.32 to land heads every time it is tossed. What is then the correct price for a gamble that pays $1 if the coin lands heads, and nothing otherwise? According to the Principal Principle, the fair price is 32 cents.
Subjectivists, also known as Bayesians or followers of epistemic probability, give the notion of probability a subjective status by regarding it as a measure of the 'degree of belief' of the individual assessing the uncertainty of a particular situation. Epistemic or subjective probability is sometimes called credence, as opposed to the term chance for a propensity probability.
Some examples of epistemic probability are to assign a probability to the proposition that a proposed law of physics is true, and to determine how probable it is that a suspect committed a crime, based on the evidence presented.
Gambling odds don't reflect the bookies' belief in a likely winner, so much as the other bettors' belief, because the bettors are actually betting against one another. The odds are set based on how many people have bet on a possible winner, so that even if the high odds players always win, the bookies will always make their percentages anyway.
The use of Bayesian probability raises the philosophical debate as to whether it can contribute valid justifications
of belief
.
Bayesians point to the work of Ramsey
and de Finetti
as proving that subjective beliefs must follow the laws of probability if they are to be coherent
.
The use of Bayesian probability involves specifying a prior probability
. This may be obtained from consideration of whether the required prior probability is greater or lesser than a reference probability associated with an urn model or a thought experiment
. The issue is that for a given problem, multiple thought experiments could apply, and choosing one is a matter of judgement: different people may assign different prior probabilities, known as the reference class problem
.
The "sunrise problem
" provides an example.
An alternative solution, is the eclectic view, which accepts both interpretations: depending on the situation, one selects one of the two interpretations for pragmatic, or principled, reasons.
but fell out of favor compared to the parametric approach, which modeled phenomena as a physical system that was observed with error, such as in celestial mechanics
.
The modern predictive approach was pioneered by Bruno de Finetti
, with the central idea of exchangeability – that future observations should behave like past observations. This view came to the attention of the Anglophone world with the 1974 translation of de Finetti's book, and has
since been propounded by such statisticians as Seymour Geisser
.
and probability axioms
for a detailed treatment.
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
has been used in a variety of ways since it was first coined in relation to games of chance. Does probability measure the real, physical tendency of something to occur, or is it just a measure of how strongly one believes it will occur? In answering such questions, we interpret the probability values of probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
.
There are two broad categories of probability interpretations which can be called 'physical' and 'evidential' probabilities. Physical probabilities, which are also called objective or frequency probabilities
Frequency probability
Frequency probability is the interpretation of probability that defines an event's probability as the limit of its relative frequency in a large number of trials. The development of the frequentist account was motivated by the problems and paradoxes of the previously dominant viewpoint, the...
, are associated with random physical systems such as roulette wheels, rolling dice and radioactive atoms. In such systems, a given type of event (such as the dice yielding a six) tends to occur at a persistent rate, or 'relative frequency', in a long run of trials. Physical probabilities either explain, or are invoked to explain, these stable frequencies. Thus talk about physical probability makes sense only when dealing with well defined random
Randomness
Randomness has somewhat differing meanings as used in various fields. It also has common meanings which are connected to the notion of predictability of events....
experiments. The two main kinds of theory of physical probability are frequentist
Frequency probability
Frequency probability is the interpretation of probability that defines an event's probability as the limit of its relative frequency in a large number of trials. The development of the frequentist account was motivated by the problems and paradoxes of the previously dominant viewpoint, the...
accounts (such as those of Venn, Reichenbach and von Mises) and propensity
Propensity probability
The propensity theory of probability is one interpretation of the concept of probability. Theorists who adopt this interpretation think of probability as a physical propensity, or disposition, or tendency of a given type of physical situation to yield an outcome of a certain kind, or to yield a...
accounts (such as those of Popper, Miller, Giere and Fetzer).
Evidential probability, also called Bayesian probability
Bayesian probability
Bayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
(or subjectivist probability), can be assigned to any statement whatsoever, even when no random process is involved, as a way to represent its subjective plausibility, or the degree to which the statement is supported by the available evidence. On most accounts, evidential probabilities are considered to be degrees of belief, defined in terms of dispositions to gamble at certain odds. The four main evidential interpretations are the classical (e.g. Laplace's) interpretation, the subjective interpretation (de Finetti and Savage), the epistemic or inductive interpretation (Ramsey
Frank P. Ramsey
Frank Plumpton Ramsey was a British mathematician who, in addition to mathematics, made significant and precocious contributions in philosophy and economics before his death at the age of 26...
, Cox) and the logical interpretation (Keynes and Carnap
Rudolf Carnap
Rudolf Carnap was an influential German-born philosopher who was active in Europe before 1935 and in the United States thereafter. He was a major member of the Vienna Circle and an advocate of logical positivism....
).
Some interpretations of probability are associated with approaches to statistical inference
Statistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
, including theories of estimation
Estimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
and hypothesis testing
Statistical hypothesis testing
A statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
. The physical interpretation, for example, is taken by followers of "frequentist" statistical methods, such as R. A. Fisher
Ronald Fisher
Sir Ronald Aylmer Fisher FRS was an English statistician, evolutionary biologist, eugenicist and geneticist. Among other things, Fisher is well known for his contributions to statistics by creating Fisher's exact test and Fisher's equation...
, Jerzy Neyman
Jerzy Neyman
Jerzy Neyman , born Jerzy Spława-Neyman, was a Polish American mathematician and statistician who spent most of his professional career at the University of California, Berkeley.-Life and career:...
and Egon Pearson
Egon Pearson
Egon Sharpe Pearson, CBE FRS was the only son of Karl Pearson, and like his father, a leading British statistician....
. Statisticians of the opposing Bayesian
Bayesian probability
Bayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
school typically accept the existence and importance of physical probabilities, but also consider the calculation of evidential probabilities to be both valid and necessary in statistics. This article, however, focuses on the interpretations of probability rather than theories of statistical inference.
The terminology of this topic is rather confusing, in part because probabilities are studied within so many different academic fields. The word "frequentist" is especially tricky. To philosophers it refers to a particular theory of physical probability, one that has more or less been abandoned. To scientists, on the other hand, "frequentist probability
Frequency probability
Frequency probability is the interpretation of probability that defines an event's probability as the limit of its relative frequency in a large number of trials. The development of the frequentist account was motivated by the problems and paradoxes of the previously dominant viewpoint, the...
" is just what philosophers call physical (or objective) probability. Those who promote Bayesian inference view "frequentist statistics" as an approach to statistical inference that recognises only physical probabilities. Also the word "objective", as applied to probability, sometimes means exactly what "physical" means here, but is also used of evidential probabilities that are fixed by rational constraints, such as logical and epistemic probabilities.
Philosophy
The philosophy of probability presents problems chiefly in matters of epistemology and the uneasy interface between mathematicalMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
concepts and ordinary language as it is used by non-mathematicians.
Probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
is an established field of study in mathematics. It has its origins in correspondence discussing the mathematics of games of chance between Blaise Pascal
Blaise Pascal
Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
and Pierre de Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
in the seventeenth century, and was formalized and rendered axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
atic as a distinct branch of mathematics by Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
in the twentieth century. In its axiomatic form, mathematical statements about probability theory carry the same sort of epistemological confidence shared by other mathematical statements in the philosophy of mathematics
Philosophy of mathematics
The philosophy of mathematics is the branch of philosophy that studies the philosophical assumptions, foundations, and implications of mathematics. The aim of the philosophy of mathematics is to provide an account of the nature and methodology of mathematics and to understand the place of...
.
The mathematical analysis originated in observations of the behaviour of game equipment such as playing card
Playing card
A playing card is a piece of specially prepared heavy paper, thin cardboard, plastic-coated paper, cotton-paper blend, or thin plastic, marked with distinguishing motifs and used as one of a set for playing card games...
s and dice
Dice
A die is a small throwable object with multiple resting positions, used for generating random numbers...
, which are designed specifically to introduce random and equalized elements; in mathematical terms, they are subjects of indifference
Principle of indifference
The principle of indifference is a rule for assigning epistemic probabilities.Suppose that there are n > 1 mutually exclusive and collectively exhaustive possibilities....
. This is not the only way probabilistic statements are used in ordinary human language: when people say that "it will probably rain", they typically do not mean that the outcome of rain versus not-rain is a random factor that the odds currently favor; instead, such statements are perhaps better understood as qualifying their expectation of rain with a degree of confidence. Likewise, when it is written that "the most probable explanation" of the name of Ludlow, Massachusetts
Ludlow, Massachusetts
Ludlow is a town in Hampden County, Massachusetts, United States. The population was 21,103 as of the 2010 census. It is located in western Massachusetts, north of Springfield, east of Chicopee, southeast of Granby, southwest of Belchertown, west of Wilbraham and is considered part of the...
"is that it was named after Roger Ludlow
Roger Ludlow
Roger Ludlow was one of the founders of the Colony of Connecticut. He was born in March 1590 in Dinton, Wiltshire, England. Roger was the second son of Sir Thomas Ludlow of Maiden Bradley, Wiltshire and Jane Pyle, sister of Sir Gabriel Pyle...
", what is meant here is not that Roger Ludlow is favored by a random factor, but rather that this is the most plausible explanation of the evidence, which admits other, less likely explanations.
Thomas Bayes
Thomas Bayes
Thomas Bayes was an English mathematician and Presbyterian minister, known for having formulated a specific case of the theorem that bears his name: Bayes' theorem...
attempted to provide a logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
that could handle varying degrees of confidence; as such, Bayesian probability
Bayesian probability
Bayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
is an attempt to recast the representation of probabilistic statements as an expression of the degree of confidence by which the beliefs they express are held.
Though probability initially may have had lowly motivations, its modern influence and use is widespread ranging from medicine, through practical pursuits
Six Sigma
Six Sigma is a business management strategy originally developed by Motorola, USA in 1986. , it is widely used in many sectors of industry.Six Sigma seeks to improve the quality of process outputs by identifying and removing the causes of defects and minimizing variability in manufacturing and...
, all the way to the higher-order and the sublime
String theory landscape
The string theory landscape or anthropic landscape refers to the large number of possible false vacua in string theory. The "landscape" includes so many possible configurations that some physicists think that the known laws of physics, the standard model and general relativity with a positive...
.
Classical definition
The first attempt at mathematical rigour in the field of probability, championed by Pierre-Simon LaplacePierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
, is now known as the classical definition. Developed from studies of games of chance (such as rolling dice
Dice
A die is a small throwable object with multiple resting positions, used for generating random numbers...
) it states that probability is shared equally between all the possible outcomes, provided these outcomes can be deemed equally likely.
If a random experiment can result in N mutually exclusive and equally likely outcomes and if NA of these outcomes result in the occurrence of the event A, the probability of A is defined by
.There are two clear limitations to the classical definition. Firstly, it is applicable only to situations in which there is only a 'finite' number of possible outcomes. But some important random experiments, such as tossing a coin
Coin
A coin is a piece of hard material that is standardized in weight, is produced in large quantities in order to facilitate trade, and primarily can be used as a legal tender token for commerce in the designated country, region, or territory....
until it rises heads, give rise to an infinite set of outcomes. And secondly, you need to determine in advance that all the possible outcomes are equally likely without relying on the notion of probability to avoid circularity—for instance, by symmetry considerations.
Frequentism
Frequentists posit that the probability of an event is its relative frequency over time, i.e., its relative frequency of occurrence after repeating a process a large number of times under similar conditions. This is also known as aleatory
Aleatory
Aleatoricism is the incorporation of chance into the process of creation, especially the creation of art or media. The word derives from the Latin word alea, the rolling of dice...
probability. The events are assumed to be governed by some random
Randomness
Randomness has somewhat differing meanings as used in various fields. It also has common meanings which are connected to the notion of predictability of events....
physical phenomena, which are either phenomena that are predictable, in principle, with sufficient information (see Determinism
Determinism
Determinism is the general philosophical thesis that states that for everything that happens there are conditions such that, given them, nothing else could happen. There are many versions of this thesis. Each of them rests upon various alleged connections, and interdependencies of things and...
); or phenomena which are essentially unpredictable. Examples of the first kind include tossing dice
Dice
A die is a small throwable object with multiple resting positions, used for generating random numbers...
or spinning a roulette
Roulette
Roulette is a casino game named after a French diminutive for little wheel. In the game, players may choose to place bets on either a single number or a range of numbers, the colors red or black, or whether the number is odd or even....
wheel; an example of the second kind is radioactive decay
Radioactive decay
Radioactive decay is the process by which an atomic nucleus of an unstable atom loses energy by emitting ionizing particles . The emission is spontaneous, in that the atom decays without any physical interaction with another particle from outside the atom...
. In the case of tossing a fair coin, frequentists say that the probability of getting a heads is 1/2, not because there are two equally likely outcomes but because repeated series of large numbers of trials demonstrate that the empirical frequency converges to the limit 1/2 as the number of trials goes to infinity.
If we denote by
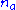the number of occurrences of an event in trials, then if 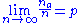we say that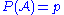 The frequentist view has its own problems. It is of course impossible to actually perform an infinity of repetitions of a random experiment to determine the probability of an event. But if only a finite number of repetitions of the process are performed, different relative frequencies will appear in different series of trials. If these relative frequencies are to define the probability, the probability will be slightly different every time it is measured. But the real probability should be the same every time. If we acknowledge the fact that we only can measure a probability with some error of measurement attached, we still get into problems as the error of measurement can only be expressed as a probability, the very concept we are trying to define. This renders even the frequency definition circular.
Logical, epistemic, and inductive probability
It is widely recognised that the term "probability" is sometimes used in contexts where it has nothing to do with physical randomness. Consider, for example, the claim that the extinction of the dinosaurs was probably caused by a large meteorite hitting the earth. Statements such as "Hypothesis H is probably true" have been interpreted to mean that the (presently available) empirical evidence (E, say) supports H to a high degree. This degree of support of H by E has been called the logical probability of H given E, or the epistemic probability of H given E, or the inductive probability of H given E.The differences between these interpretations are rather small, and may seem inconsequential. One of the main points of disagreement lies in the relation between probability and belief. Logical probabilities are conceived to be objective, logical relations between propositions (or sentences), and hence not to depend in any way upon belief. They are degrees of (partial) entailment
Entailment
In logic, entailment is a relation between a set of sentences and a sentence. Let Γ be a set of one or more sentences; let S1 be the conjunction of the elements of Γ, and let S2 be a sentence: then, Γ entails S2 if and only if S1 and not-S2 are logically inconsistent...
, or degrees of logical consequence, not degrees of belief
Belief
Belief is the psychological state in which an individual holds a proposition or premise to be true.-Belief, knowledge and epistemology:The terms belief and knowledge are used differently in philosophy....
. (They do, nevertheless, dictate proper degrees of belief, as is discussed below.) Frank P. Ramsey
Frank P. Ramsey
Frank Plumpton Ramsey was a British mathematician who, in addition to mathematics, made significant and precocious contributions in philosophy and economics before his death at the age of 26...
, on the other hand, was skeptical about the existence of such objective logical relations and argued that (evidential) probability is "the logic of partial belief" ("Truth and Probability", 1926, p. 157). In other words, Ramsey held that epistemic probabilities simply are degrees of rational belief, rather than being logical relations that merely constrain degrees of rational belief.
Another point of disagreement concerns the uniqueness of evidential probability, relative to a given state of knowledge. Rudolf Carnap
Rudolf Carnap
Rudolf Carnap was an influential German-born philosopher who was active in Europe before 1935 and in the United States thereafter. He was a major member of the Vienna Circle and an advocate of logical positivism....
held, for example, that logical principles always determine a unique logical probability for any statement, relative to any body of evidence. Ramsey, by contrast, thought that while degrees of belief are subject to some rational constraints (such as, but not limited to, the axioms of probability) these constraints usually do not determine a unique value. Rational people, in other words, may differ somewhat in their degrees of belief, even if they all have the same information.
Propensity
Propensity theorists think of probability as a physical propensity, or disposition, or tendency of a given type of physical situation to yield an outcome of a certain kind or to yield a long run relative frequency of such an outcome. This kind of objective probability is sometimes called 'chance'.Propensities, or chances, are not relative frequencies, but purported causes of the observed stable relative frequencies. Propensities are invoked to explain why repeating a certain kind of experiment will generate a given outcome type at a persistent rate, which are known as propensities or chances. Frequentists are unable to take this approach, since relative frequencies do not exist for single tosses of a coin, but only for large ensembles or collectives. In contrast, a propensitist is able to use the law of large numbers
Law of large numbers
In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
to explain the behaviour of long-run frequencies. This law, which is a consequence of the axioms of probability, says that if (for example) a coin is tossed repeatedly many times, in such a way that its probability of landing heads is the same on each toss, and the outcomes are probabilistically independent, then the relative frequency of heads will (with high probability) be close to the probability of heads on each single toss. This law allows that stable long-run frequencies are a manifestation of invariant single-case probabilities. In addition to explaining the emergence of stable relative frequencies, the idea of propensity is motivated by the desire to make sense of single-case probability attributions in quantum mechanics, such as the probability of decay
Radioactive decay
Radioactive decay is the process by which an atomic nucleus of an unstable atom loses energy by emitting ionizing particles . The emission is spontaneous, in that the atom decays without any physical interaction with another particle from outside the atom...
of a particular atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
at a particular time.
The main challenge facing propensity theories is to say exactly what propensity means. (And then, of course, to show that propensity thus defined has the required properties.) At present, unfortunately, none of the well-recognised accounts of propensity comes close to meeting this challenge.
A propensity theory of probability was given by Charles Sanders Peirce. A later propensity theory was proposed by philosopher Karl Popper
Karl Popper
Sir Karl Raimund Popper, CH FRS FBA was an Austro-British philosopher and a professor at the London School of Economics...
, who had only slight acquaintance with the writings of C. S. Peirce, however. Popper noted that the outcome of a physical experiment is produced by a certain set of "generating conditions". When we repeat an experiment, as the saying goes, we really perform another experiment with a (more or less) similar set of generating conditions. To say that a set of generating conditions has propensity p of producing the outcome E means that those exact conditions, if repeated indefinitely, would produce an outcome sequence in which E occurred with limiting relative frequency p. For Popper then, a deterministic experiment would have propensity 0 or 1 for each outcome, since those generating conditions would have same outcome on each trial. In other words, non-trivial propensities (those that differ from 0 and 1) only exist for genuinely indeterministic experiments.
A number of other philosophers, including David Miller
David Miller (philosopher)
David W. Miller is a philosopher and prominent exponent of critical rationalism. He taught in the Department of Philosophy at the University of Warwick in Coventry, UK....
and Donald A. Gillies
Donald A. Gillies
Donald A. Gillies is a British philosopher and historian of science and mathematics. He is an Emeritus Professor in the Department of Science and Technology Studies at University College, London.-Career:...
, have proposed propensity theories somewhat similar to Popper's.
Other propensity theorists (e.g. Ronald Giere) do not explicitly define propensities at all, but rather see propensity as defined by the theoretical role it plays in science. They argue, for example, that physical magnitudes such as electrical charge cannot be explicitly defined either, in terms of more basic things, but only in terms of what they do (such as attracting and repelling other electrical charges). In a similar way, propensity is whatever fills the various roles that physical probability plays in science.
What roles does physical probability play in science? What are its properties? One central property of chance is that, when known, it constrains rational belief to take the same numerical value. David Lewis called this the Principal Principle, a term that philosophers have mostly adopted. For example, suppose you are certain that a particular biased coin has propensity 0.32 to land heads every time it is tossed. What is then the correct price for a gamble that pays $1 if the coin lands heads, and nothing otherwise? According to the Principal Principle, the fair price is 32 cents.
Subjectivism
Subjectivists, also known as Bayesians or followers of epistemic probability, give the notion of probability a subjective status by regarding it as a measure of the 'degree of belief' of the individual assessing the uncertainty of a particular situation. Epistemic or subjective probability is sometimes called credence, as opposed to the term chance for a propensity probability.
Some examples of epistemic probability are to assign a probability to the proposition that a proposed law of physics is true, and to determine how probable it is that a suspect committed a crime, based on the evidence presented.
Gambling odds don't reflect the bookies' belief in a likely winner, so much as the other bettors' belief, because the bettors are actually betting against one another. The odds are set based on how many people have bet on a possible winner, so that even if the high odds players always win, the bookies will always make their percentages anyway.
The use of Bayesian probability raises the philosophical debate as to whether it can contribute valid justifications
Theory of justification
Theory of justification is a part of epistemology that attempts to understand the justification of propositions and beliefs. Epistemologists are concerned with various epistemic features of belief, which include the ideas of justification, warrant, rationality, and probability...
of belief
Belief
Belief is the psychological state in which an individual holds a proposition or premise to be true.-Belief, knowledge and epistemology:The terms belief and knowledge are used differently in philosophy....
.
Bayesians point to the work of Ramsey
Frank P. Ramsey
Frank Plumpton Ramsey was a British mathematician who, in addition to mathematics, made significant and precocious contributions in philosophy and economics before his death at the age of 26...
and de Finetti
Bruno de Finetti
Bruno de Finetti was an Italian probabilist, statistician and actuary, noted for the "operational subjective" conception of probability...
as proving that subjective beliefs must follow the laws of probability if they are to be coherent
Coherence (physics)
In physics, coherence is a property of waves that enables stationary interference. More generally, coherence describes all properties of the correlation between physical quantities of a wave....
.
The use of Bayesian probability involves specifying a prior probability
Prior probability
In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
. This may be obtained from consideration of whether the required prior probability is greater or lesser than a reference probability associated with an urn model or a thought experiment
Thought experiment
A thought experiment or Gedankenexperiment considers some hypothesis, theory, or principle for the purpose of thinking through its consequences...
. The issue is that for a given problem, multiple thought experiments could apply, and choosing one is a matter of judgement: different people may assign different prior probabilities, known as the reference class problem
Reference class problem
In statistics, the reference class problem is the problem of deciding what class to use when calculating the probability applicable to a particular case...
.
The "sunrise problem
Sunrise problem
The sunrise problem can be expressed as follows: "What is the probability that the sun will rise tomorrow?"The sunrise problem illustrates the difficulty of using probability theory when evaluating the plausibility of statements or beliefs....
" provides an example.
Practical controversy
This difference in point of view has also many implications both for the methods by which statistics is practiced, and for the way in which conclusions are expressed. When comparing two hypotheses and using some information, frequency methods would typically result in the rejection or non-rejection of the original hypothesis at a particular significance level, and frequentists would all agree that the hypothesis should be rejected or not at that level of significance. However, there is no normative methodology to choose levels of significance. Bayesian methods would suggest that one hypothesis was more probable than the other, but individual Bayesians might differ about which was the more probable and by how much, by virtue of having used different priors; but that's the same thing as disagreeing on significance levels, except significance levels are just an ad hoc device which are not really a probability, while priors are not only justified by the rules of probability, but there is definitely a normative methodology to define beliefs; so even if a Bayesian wanted to express complete ignorance (as a frequentist claims to do but does it wrong), they could do it with the maximum entropy principle, which assigns equal probabilities to all possible values when the space is finite and discrete; there may be debate on what to do for infinite spaces or when there's uncertainty about the size of the sample space. The most important distinction between the frequentist and Bayesian paradigms, is that frequentist makes strong distinctions between probability, statistics, and decision-making, whereas Bayesians unify decision-making, statistics and probability under a single philosophically and mathematically consistent framework, unlike the frequentist paradigm which has been proven to be inconsistent, especially for real-world situations where experiments (or "random events") can not be repeated more than once. Bayesians would argue that this is right and proper — if the issue is such that reasonable people can put forward different, but plausible, priors and the data are such that the likelihood does not swamp the prior, then the issue is not resolved unambiguously at the present stage of knowledge and Bayesian statistics highlights this fact. They would argue that any approach that purports to produce a single, definitive answer to the question at hand in these circumstances is obscuring the truth. But "frequentists" do not claim to produce "a single, definitive answer to the question at hand".An alternative solution, is the eclectic view, which accepts both interpretations: depending on the situation, one selects one of the two interpretations for pragmatic, or principled, reasons.
Prediction
An alternative account of probability emphasizes the role of prediction – predicting future observations on the basis of past observations, not on unobservable parameters. In its modern form, it is mainly in the Bayesian vein. This was the main function of probability before the 20th century,but fell out of favor compared to the parametric approach, which modeled phenomena as a physical system that was observed with error, such as in celestial mechanics
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
.
The modern predictive approach was pioneered by Bruno de Finetti
Bruno de Finetti
Bruno de Finetti was an Italian probabilist, statistician and actuary, noted for the "operational subjective" conception of probability...
, with the central idea of exchangeability – that future observations should behave like past observations. This view came to the attention of the Anglophone world with the 1974 translation of de Finetti's book, and has
since been propounded by such statisticians as Seymour Geisser
Seymour Geisser
Seymour Geisser was a statistician noted for emphasizing the role of prediction in statistical inference – see predictive inference. In his book , he held that conventional statistical inference about unobservable population parameters amounts to inference about things that do not exist,...
.
Axiomatic probability
The mathematics of probability can be developed on an entirely axiomatic basis that is independent of any interpretation: see the articles on probability theoryProbability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and probability axioms
Probability axioms
In probability theory, the probability P of some event E, denoted P, is usually defined in such a way that P satisfies the Kolmogorov axioms, named after Andrey Kolmogorov, which are described below....
for a detailed treatment.
See also
- Philosophy of statisticsPhilosophy of statisticsThe philosophy of statistics involves the meaning, justification, utility, use and abuse of statistics and its methodology, and ethical and epistemological issues involved in the consideration of choice and interpretation of data and methods of Statistics....
- Frequency (statistics)Frequency (statistics)In statistics the frequency of an event i is the number ni of times the event occurred in the experiment or the study. These frequencies are often graphically represented in histograms....
- Negative probabilityNegative probabilityIn 1942, Paul Dirac wrote a paper "The Physical Interpretation of Quantum Mechanics" where he introduced the concept of negative energies and negative probabilities:...
- Pignistic probabilityPignistic probabilityPignistic probability, in decision theory, is a probability that a rational person will assign to an option when required to make a decision.A person may have, at one level certain beliefs or a lack of knowledge, or uncertainty, about the options and their actual likelihoods...
- Sunrise problemSunrise problemThe sunrise problem can be expressed as follows: "What is the probability that the sun will rise tomorrow?"The sunrise problem illustrates the difficulty of using probability theory when evaluating the plausibility of statements or beliefs....
- Probability amplitudeProbability amplitudeIn quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
(quantum mechanics)
Further reading
- Laurence Jonathan CohenLaurence Jonathan CohenJonathan Cohen FBA was a British philosopher. He was Fellow and Praelector in Philosophy, 1957–90 and Senior Tutor, 1985–90 at The Queen's College, Oxford and British Academy Reader in Humanities, University of Oxford, 1982–84.Education: St...
(1989) An Introduction to the Philosophy of Induction and Probability. Oxford Univ. Press. - Donald A. GilliesDonald A. GilliesDonald A. Gillies is a British philosopher and historian of science and mathematics. He is an Emeritus Professor in the Department of Science and Technology Studies at University College, London.-Career:...
(2000) Philosophical Theories of Probability. London: Routledge. (a comprehensive monograph covering the four principal current interpretations: logical, subjective, frequency, propensity) - Antony Eagle, ed. (2011) "Philosophy of Probability: Contemporary Readings". London: Routledge.
- Ian HackingIan HackingIan Hacking, CC, FRSC, FBA is a Canadian philosopher, specializing in the philosophy of science.- Life and works :...
(1975) Emergence of Probability. - Paul HumphreysPaul HumphreysPaul Humphreys is a British musician.-Life and career:He is best known as a member of synth pop group Orchestral Manoeuvres in the Dark , which he founded with Andy McCluskey in 1978.He grew up on the Wirral Peninsula in North West England, during which time he developed his interest in German...
, ed. (1994) Patrick SuppesPatrick SuppesPatrick Colonel Suppes is an American philosopher who has made significant contributions to philosophy of science, the theory of measurement, the foundations of quantum mechanics, decision theory, psychology, and educational technology...
: Scientific Philosopher, Synthese Library, Springer-Verlag.- Vol. 1: Probability and Probabilistic Causality.
- Vol. 2: Philosophy of Physics, Theory Structure and Measurement, and Action Theory.
- Jackson, Frank, and Robert Pargetter (1982) "Physical Probability as a Propensity," Noûs 16(4): 567–583.
- Andrei Khrennikov (2009) Interpretations of probability (2nd ed.) Walter de Gruyter (covers mostly non-Kolmogorov probability models, particularly with respect to quantum physics)
- David LewisDavid Kellogg LewisDavid Kellogg Lewis was an American philosopher. Lewis taught briefly at UCLA and then at Princeton from 1970 until his death. He is also closely associated with Australia, whose philosophical community he visited almost annually for more than thirty years...
(1986) Philosophical Papers, Vol. II. Oxford Univ. Press. - Brian SkyrmsBrian SkyrmsBrian Skyrms is a Distinguished Professor of Logic and Philosophy of Science and Economics at the University of California, Irvine and a Professor of Philosophy at Stanford University. He has worked on problems in the philosophy of science, causation, decision theory, game theory, and the...
(2000) Choice and Chance, 4th ed. Wadsworth. - Jan Von Plato (1994) Creating Modern Probability. Cambridge University Press.
External links
- Interpretations of Probability at the Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...