Upper and lower probabilities
Encyclopedia
Upper and lower probabilities are representations of imprecise probability
. Whereas probability theory
uses a single number, the probability
, to describe how likely an event is to occur, this method uses two numbers: the upper probability of the event and the lower probability of the event.
Because frequentist statistics disallows metaprobabilities, frequentists have had to propose new solutions. Cedric Smith and Arthur Dempster
each developed a theory of upper and lower probabilities. Glenn Shafer developed Dempster's theory further, and it is now known as Dempster–Shafer theory: see also Choquet(1953).
More precisely, in the work of these authors one considers in a power set,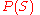
, a mass function 
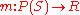satisfying the conditions
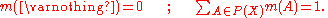
In turn, a mass is associated with two non-additive continuous measures called belief and plausibility defined as follows:
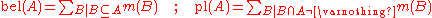
In the case where
is infinite there can be 
such that there is no associated mass function. See p. 36 of Halpern (2003). Probability measures are a special case of belief functions in which the mass function assigns positive mass to singletons of the event space only.
A different notion of upper and lower probabilities is obtained by the lower and upper envelopes obtained from a class C of probability distributions by setting
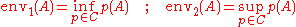
The upper and lower probabilities are also related with probabilistic logic
: see Gerla (1994).
Observe also that a necessity measure can be seen as a lower probability and a possibility measure can be seen as an upper probability.
Imprecise probability
Imprecise probability generalizes probability theory to allow for partial probability specifications, and is applicable when information is scarce, vague, or conflicting, in which case a unique probability distribution may be hard to identify...
. Whereas probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
uses a single number, the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, to describe how likely an event is to occur, this method uses two numbers: the upper probability of the event and the lower probability of the event.
Because frequentist statistics disallows metaprobabilities, frequentists have had to propose new solutions. Cedric Smith and Arthur Dempster
Arthur P. Dempster
Arthur Pentland Dempster is a Professor Emeritus in the Harvard University Department of Statistics. He was one of four faculty when the department was founded in 1957.He was a Putnam Fellow in 1951. He obtained his Ph.D. from Princeton University in 1956...
each developed a theory of upper and lower probabilities. Glenn Shafer developed Dempster's theory further, and it is now known as Dempster–Shafer theory: see also Choquet(1953).
More precisely, in the work of these authors one considers in a power set,
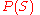, a mass function 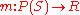satisfying the conditions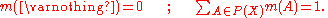In turn, a mass is associated with two non-additive continuous measures called belief and plausibility defined as follows:
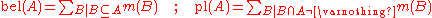
In the case where
is infinite there can be such that there is no associated mass function. See p. 36 of Halpern (2003). Probability measures are a special case of belief functions in which the mass function assigns positive mass to singletons of the event space only.A different notion of upper and lower probabilities is obtained by the lower and upper envelopes obtained from a class C of probability distributions by setting
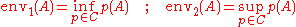
The upper and lower probabilities are also related with probabilistic logic
Probabilistic logic
The aim of a probabilistic logic is to combine the capacity of probability theory to handle uncertainty with the capacity of deductive logic to exploit structure. The result is a richer and more expressive formalism with a broad range of possible application areas...
: see Gerla (1994).
Observe also that a necessity measure can be seen as a lower probability and a possibility measure can be seen as an upper probability.
See also
- Possibility theoryPossibility theoryPossibility theory is a mathematical theory for dealing with certain types of uncertainty and is an alternative to probability theory. Professor Lotfi Zadeh first introduced possibility theory in 1978 as an extension of his theory of fuzzy sets and fuzzy logic. D. Dubois and H. Prade further...
- Probability theoryProbability theoryProbability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
- Fuzzy measure theoryFuzzy measure theoryFuzzy measure theory considers a number of special classes of measures, each of which is characterized by a special property. Some of the measures used in this theory are plausibility and belief measures, fuzzy set membership function and the classical probability measures...
- Interval finite elementInterval finite elementThe interval finite element method is a finite element method that uses interval parameters. Interval FEM can be applied in situations where it is not possible to get reliable probabilistic characteristics of the structure. This is important in concrete structures, wood structures, geomechanics,...