Spectrum of a theory
Encyclopedia
In model theory
, a branch of mathematical logic
, the spectrum of a theory
is given by the number of isomorphism classes of models in various cardinalities. More precisely,
for any complete theory
T in a language we write I(T, α) for the number of models of T (up to isomorphism) of cardinality α. The spectrum problem is to describe the possible behaviors of I(T, α) as a function of α. It has been almost completely solved for the case of a countable theory T.
The Löwenheim–Skolem theorem
shows that if I(T, α) is nonzero for one infinite cardinal then it is nonzero for all of them.
Morley's categoricity theorem
was the first main step in solving the spectrum problem: it states that if I(T, α) is 1 for some uncountable α then it is 1 for all uncountable α.
Robert Vaught showed that I(T,ω) cannot be 2. It is easy to find examples where it is any given non-negative integer other than 2. Morley proved that if I(T,ω) is infinite then it must be ℵ0
or ℵ1 or the cardinality of the continuum. It is not known if it can be ℵ1 if the continuum hypothesis
is false: this is called the Vaught conjecture
and is
the main remaining open problem (in 2005) in the theory of the spectrum.
Morley's problem is a conjecture
(first proposed by Michael D. Morley
) in mathematical logic
that I(T, α) is nondecreasing
in α for uncountable α. This was proved by Saharon Shelah
. For this, he proved a very deep dichotomy theorem.
Saharon Shelah gave an almost complete solution to the spectrum problem. For a given complete theory T, either I(T, α) = 2α for all uncountable α, or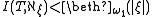
(See aleph number
and beth number
for an explanation of the notation) for all ordinals ξ, which is usually much smaller than the bound in the first case. Roughly speaking this says that either there are the maximum possible number of models in all uncountable cardinalities, or there are only "few" models in all uncountable cardinalities. Shelah also gave a description of the possible spectra in the case when there are few models.
, Michael C. Laskowski gave the following complete solution to the spectrum problem for countable theories in uncountable cardinalities.
If T is a countable complete theory, then the number I(T, ℵα) of isomorphism classes of models is given for ordinals α>0 by the minimum of 2ℵα and one of the following maps:
Moreover, all possibilities above occur as the spectrum of some countable complete theory.
The number d in the list above is the depth of the theory.
If T is a theory we define a new theory 2T to be the theory with an equivalence relation such that there are infinitely many equivalence classes each of which is a model of T. We also define theories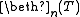
by 
, 
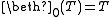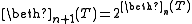. Then
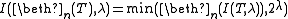. This can be used to construct examples of theories with spectra in the list above for non-minimal values of d from examples for the minimal value of d.
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, a branch of mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, the spectrum of a theory
is given by the number of isomorphism classes of models in various cardinalities. More precisely,
for any complete theory
Complete theory
In mathematical logic, a theory is complete if it is a maximal consistent set of sentences, i.e., if it is consistent, and none of its proper extensions is consistent...
T in a language we write I(T, α) for the number of models of T (up to isomorphism) of cardinality α. The spectrum problem is to describe the possible behaviors of I(T, α) as a function of α. It has been almost completely solved for the case of a countable theory T.
Early results
In this section T is a countable complete theory.The Löwenheim–Skolem theorem
Löwenheim–Skolem theorem
In mathematical logic, the Löwenheim–Skolem theorem, named for Leopold Löwenheim and Thoralf Skolem, states that if a countable first-order theory has an infinite model, then for every infinite cardinal number κ it has a model of size κ...
shows that if I(T, α) is nonzero for one infinite cardinal then it is nonzero for all of them.
Morley's categoricity theorem
Morley's categoricity theorem
In model theory, a branch of mathematical logic, a theory is κ-categorical if it has exactly one model of cardinality κ up to isomorphism....
was the first main step in solving the spectrum problem: it states that if I(T, α) is 1 for some uncountable α then it is 1 for all uncountable α.
Robert Vaught showed that I(T,ω) cannot be 2. It is easy to find examples where it is any given non-negative integer other than 2. Morley proved that if I(T,ω) is infinite then it must be ℵ0
or ℵ1 or the cardinality of the continuum. It is not known if it can be ℵ1 if the continuum hypothesis
Continuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
is false: this is called the Vaught conjecture
Vaught conjecture
The Vaught conjecture is a conjecture in the mathematical field of model theory originally proposed by Robert Lawson Vaught in 1961. It states that the number of countable models of a first-order complete theory in a countable language is finite or ℵ0 or 2ℵ0...
and is
the main remaining open problem (in 2005) in the theory of the spectrum.
Morley's problem is a conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
(first proposed by Michael D. Morley
Michael D. Morley
Michael Darwin Morley is an American mathematician, currently professor emeritus at Cornell University.His research is in advanced mathematical logic and model theory, and he is best known for Morley's categoricity theorem, which he proved in his Ph.D. thesis "Categoricity in Power" in 1962.His...
) in mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
that I(T, α) is nondecreasing
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
in α for uncountable α. This was proved by Saharon Shelah
Saharon Shelah
Saharon Shelah is an Israeli mathematician. He is a professor of mathematics at the Hebrew University of Jerusalem and Rutgers University in New Jersey.-Biography:...
. For this, he proved a very deep dichotomy theorem.
Saharon Shelah gave an almost complete solution to the spectrum problem. For a given complete theory T, either I(T, α) = 2α for all uncountable α, or
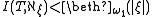(See aleph numberAleph number
In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
and beth number
Beth number
In mathematics, the infinite cardinal numbers are represented by the Hebrew letter \aleph indexed with a subscript that runs over the ordinal numbers...
for an explanation of the notation) for all ordinals ξ, which is usually much smaller than the bound in the first case. Roughly speaking this says that either there are the maximum possible number of models in all uncountable cardinalities, or there are only "few" models in all uncountable cardinalities. Shelah also gave a description of the possible spectra in the case when there are few models.
List of possible spectra of a countable theory
By extending Shelah's work, Bradd Hart, Ehud HrushovskiEhud Hrushovski
Ehud Hrushovski is a mathematical logician. He is a Professor of Mathematics at the Hebrew University of Jerusalem.His father, Benjamin Harshav, is Emeritus Professor in Yale University and Tel Aviv University to Comparative Literature and a poet....
, Michael C. Laskowski gave the following complete solution to the spectrum problem for countable theories in uncountable cardinalities.
If T is a countable complete theory, then the number I(T, ℵα) of isomorphism classes of models is given for ordinals α>0 by the minimum of 2ℵα and one of the following maps:
- 2ℵα. Examples: there are many examples, in particular any unclassifiable or deep theory, such as the theory of the random graphRandom graphIn mathematics, a random graph is a graph that is generated by some random process. The theory of random graphs lies at the intersection between graph theory and probability theory, and studies the properties of typical random graphs.-Random graph models:...
. 
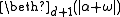for some countable infinite ordinal d. (For finite d see case 8.) Examples: The theory with equivalence relations Eβ for all β with β+1<d, such that every Eγ class is a union of infinitely many Eβ classes, and each E0 class is infinite.
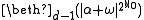for some finite positive ordinal d. Example (for d=1): the theory of countably many independent unary predicates.
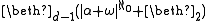for some finite positive ordinal d.
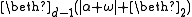for some finite positive ordinal d;
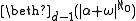for some finite positive ordinal d. Example (for d=1): the theory of countable many disjoint unary predicates.
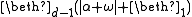for some finite ordinal d≥2;
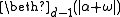for some finite positive ordinal d;
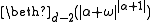for some finite ordinal d≥2; Examples: similar to case 2.
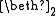. Example: the theory of the integers viewed as an abelian group.
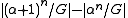for finite α, and |α| for infinite α, where G is some subgroup of the symmetric group on n ≥ 2 elements. Here, we identify αn with the set of sequences of length n of elements of a set of size α. G actsGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on αn by permuting the sequence elements, and |αn/G| denotes the number of orbits of this action. Examples: the theory of the set ω×n acted on by the wreath productWreath productIn mathematics, the wreath product of group theory is a specialized product of two groups, based on a semidirect product. Wreath products are an important tool in the classification of permutation groups and also provide a way of constructing interesting examples of groups.Given two groups A and H...
of G with all permutations of ω.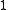
. Examples: theories that are categorical in uncountable cardinals, such as the theory of algebraically closed fields in a given characteristic.
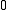. Examples: theories with a finite model, and the inconsistent theory.
Moreover, all possibilities above occur as the spectrum of some countable complete theory.
The number d in the list above is the depth of the theory.
If T is a theory we define a new theory 2T to be the theory with an equivalence relation such that there are infinitely many equivalence classes each of which is a model of T. We also define theories
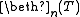by 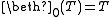, 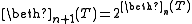. Then 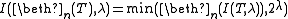. This can be used to construct examples of theories with spectra in the list above for non-minimal values of d from examples for the minimal value of d.