Split-radix FFT algorithm
Encyclopedia
The split-radix FFT is a fast Fourier transform
(FFT) algorithm for computing the discrete Fourier transform
(DFT), and was first described in an initially little-appreciated paper by R. Yavne (1968) and subsequently rediscovered simultaneously by various authors in 1984. (The name "split radix" was coined by two of these reinventors, P. Duhamel and H. Hollmann.) In particular, split radix is a variant of the Cooley-Tukey FFT algorithm
that uses a blend of radices 2 and 4: it recursively
expresses a DFT of length N in terms of one smaller DFT of length N/2 and two smaller DFTs of length N/4.
The split-radix FFT, along with its variations, long had the distinction of achieving the lowest published arithmetic operation count (total exact number of required real
additions and multiplications) to compute a DFT of power-of-two
sizes N. The arithmetic count of the original split-radix algorithm was improved upon in 2004 (with the initial gains made in unpublished work by J. Van Buskirk via hand optimization for N=64 http://groups.google.com/group/comp.dsp/msg/9e002292accb8a8b http://home.comcast.net/~kmbtib/), but it turns out that one can still achieve the new lowest count by a modification of split radix (Johnson and Frigo, 2007). Although the number of arithmetic operations is not the sole factor (or even necessarily the dominant factor) in determining the time required to compute a DFT on a computer
, the question of the minimum possible count is of longstanding theoretical interest. (No tight lower bound on the operation count has currently been proven.)
The split-radix algorithm can only be applied when N is a multiple of 4, but since it breaks a DFT into smaller DFTs it can be combined with any other FFT algorithm as desired.
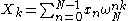
where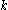
is an integer ranging from 
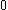to 
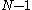and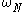 
denotes the primitive root of unity
:
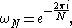
and thus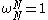
.
The split-radix algorithm works by expressing this summation in terms of three smaller summations. (Here, we give the "decimation in time" version of the split-radix FFT; the dual decimation in frequency version is essentially just the reverse of these steps.)
First, a summation over the even
indices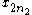
. Second, a summation over the odd indices broken into two pieces: 
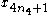and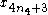 
, according to whether the index is 1 or 3 modulo
4. Here,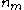
denotes an index that runs from 0 to 
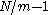. The resulting summations look like:
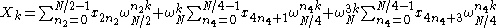
where we have used the fact that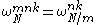
. These three sums correspond to portions of radix-2 (size N/2) and radix-4 (size N/4) Cooley-Tukey steps, respectively. (The underlying idea is that the even-index subtransform of radix-2 has no multiplicative factor in front of it, so it should be left as-is, while the odd-index subtransform of radix-2 benefits by combining a second recursive subdivision.)
These smaller summations are now exactly DFTs of length N/2 and N/4, which can be performed recursively and then recombined.
More specifically, let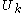
denote the result of the DFT of length N/2 (for 
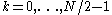), and let 
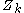and 
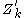denote the results of the DFTs of length N/4 (for 
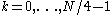). Then the output 
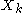is simply: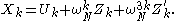
This, however, performs unnecessary calculations, since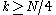
turn out to share many calculations with 
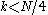. In particular, if we add N/4 to k, the size-N/4 DFTs are not changed (because they are periodic in k), while the size-N/2 DFT is unchanged if we add N/2 to k. So, the only things that change are the 
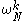and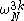 
terms, known as twiddle factor
s. Here, we use the identities: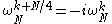
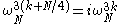
to finally arrive at: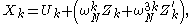
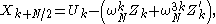
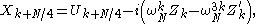
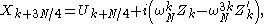
which gives all of the outputs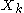
if we let 
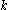range from 
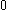to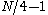 
in the above four expressions.
Notice that these expressions are arranged so that we need to combine the various DFT outputs by pairs of additions and subtractions, which are known as butterflies
. In order to obtain the minimal operation count for this algorithm, one needs to take into account special cases for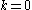
(where the twiddle factors are unity) and for 
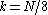(where the twiddle factors are 
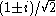and can be multiplied more quickly); see, e.g. Sorensen et al. (1986). Multiplications by 
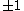and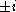 
are ordinarily counted as free (all negations can be absorbed by converting additions into subtractions or vice versa).
This decomposition is performed recursively when N is a power of two. The base cases of the recursion are N=1, where the DFT is just a copy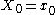
, and N=2, where the DFT is an addition 
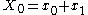and a subtraction 
.
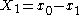These considerations result in a count: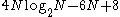
real additions and multiplications, for N>1 a power of two. This count assumes that, for odd powers of 2, the leftover factor of 2 (after all the split-radix steps, which divide N by 4) is handled directly by the DFT definition (4 real additions and multiplications), or equivalently by a radix-2 Cooley–Tukey FFT step.
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT) algorithm for computing the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
(DFT), and was first described in an initially little-appreciated paper by R. Yavne (1968) and subsequently rediscovered simultaneously by various authors in 1984. (The name "split radix" was coined by two of these reinventors, P. Duhamel and H. Hollmann.) In particular, split radix is a variant of the Cooley-Tukey FFT algorithm
Cooley-Tukey FFT algorithm
The Cooley–Tukey algorithm, named after J.W. Cooley and John Tukey, is the most common fast Fourier transform algorithm. It re-expresses the discrete Fourier transform of an arbitrary composite size N = N1N2 in terms of smaller DFTs of sizes N1 and N2, recursively, in order to reduce the...
that uses a blend of radices 2 and 4: it recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
expresses a DFT of length N in terms of one smaller DFT of length N/2 and two smaller DFTs of length N/4.
The split-radix FFT, along with its variations, long had the distinction of achieving the lowest published arithmetic operation count (total exact number of required real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
additions and multiplications) to compute a DFT of power-of-two
Power of two
In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
sizes N. The arithmetic count of the original split-radix algorithm was improved upon in 2004 (with the initial gains made in unpublished work by J. Van Buskirk via hand optimization for N=64 http://groups.google.com/group/comp.dsp/msg/9e002292accb8a8b http://home.comcast.net/~kmbtib/), but it turns out that one can still achieve the new lowest count by a modification of split radix (Johnson and Frigo, 2007). Although the number of arithmetic operations is not the sole factor (or even necessarily the dominant factor) in determining the time required to compute a DFT on a computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
, the question of the minimum possible count is of longstanding theoretical interest. (No tight lower bound on the operation count has currently been proven.)
The split-radix algorithm can only be applied when N is a multiple of 4, but since it breaks a DFT into smaller DFTs it can be combined with any other FFT algorithm as desired.
Split-radix decomposition
Recall that the DFT is defined by the formula: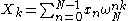where
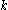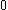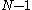is an integer ranging from to and 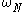denotes the primitive root of unityRoot of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
:
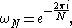
and thus
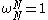.The split-radix algorithm works by expressing this summation in terms of three smaller summations. (Here, we give the "decimation in time" version of the split-radix FFT; the dual decimation in frequency version is essentially just the reverse of these steps.)
First, a summation over the even
Even and odd numbers
In mathematics, the parity of an object states whether it is even or odd.This concept begins with integers. An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without remainder; an odd number is an integer that is not evenly divisible by 2...
indices
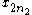. Second, a summation over the odd indices broken into two pieces: 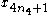and 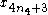, according to whether the index is 1 or 3 moduloModulo operation
In computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
4. Here,
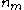denotes an index that runs from 0 to 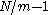. The resulting summations look like: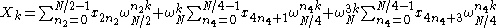where we have used the fact that
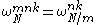. These three sums correspond to portions of radix-2 (size N/2) and radix-4 (size N/4) Cooley-Tukey steps, respectively. (The underlying idea is that the even-index subtransform of radix-2 has no multiplicative factor in front of it, so it should be left as-is, while the odd-index subtransform of radix-2 benefits by combining a second recursive subdivision.)These smaller summations are now exactly DFTs of length N/2 and N/4, which can be performed recursively and then recombined.
More specifically, let
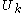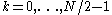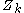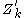denote the result of the DFT of length N/2 (for ), and let and denote the results of the DFTs of length N/4 (for 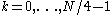). Then the output 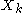is simply: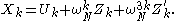This, however, performs unnecessary calculations, since
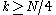turn out to share many calculations with 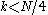. In particular, if we add N/4 to k, the size-N/4 DFTs are not changed (because they are periodic in k), while the size-N/2 DFT is unchanged if we add N/2 to k. So, the only things that change are the 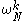and 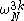terms, known as twiddle factorTwiddle factor
A twiddle factor, in fast Fourier transform algorithms, is any of the trigonometric constant coefficients that are multiplied by the data in the course of the algorithm...
s. Here, we use the identities:
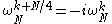
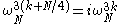
to finally arrive at:
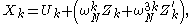
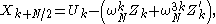
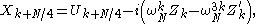
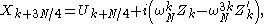
which gives all of the outputs
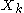if we let 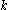range from 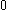to 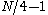in the above four expressions.Notice that these expressions are arranged so that we need to combine the various DFT outputs by pairs of additions and subtractions, which are known as butterflies
Butterfly diagram
In the context of fast Fourier transform algorithms, a butterfly is a portion of the computation that combines the results of smaller discrete Fourier transforms into a larger DFT, or vice versa . The name "butterfly" comes from the shape of the data-flow diagram in the radix-2 case, as described...
. In order to obtain the minimal operation count for this algorithm, one needs to take into account special cases for
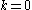(where the twiddle factors are unity) and for 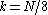(where the twiddle factors are 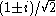and can be multiplied more quickly); see, e.g. Sorensen et al. (1986). Multiplications by 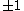and 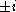are ordinarily counted as free (all negations can be absorbed by converting additions into subtractions or vice versa).This decomposition is performed recursively when N is a power of two. The base cases of the recursion are N=1, where the DFT is just a copy
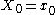, and N=2, where the DFT is an addition 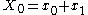and a subtraction 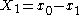.These considerations result in a count:
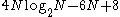real additions and multiplications, for N>1 a power of two. This count assumes that, for odd powers of 2, the leftover factor of 2 (after all the split-radix steps, which divide N by 4) is handled directly by the DFT definition (4 real additions and multiplications), or equivalently by a radix-2 Cooley–Tukey FFT step.