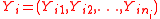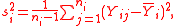Standardized mean of a contrast variable
Encyclopedia
In statistics
, the standardized mean of a contrast variable (SMCV or SMC), is a parameter assessing effect size
. The SMCV is defined as mean
divided by the standard deviation
of a contrast variable
.
The SMCV was first proposed for one-way ANOVA cases
and was then extended to multi-factor ANOVA cases
.
The standardized mean of a contrast variable, along with c+-probability
, can provide a consistent interpretation of the strength of a comparison. When there are only two groups involved in a comparison, SMCV is the same as SSMD. SSMD belongs to a popular type of effect-size measure called "standardized mean differences" which includes Cohen's and Glass's
and Glass's 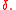
In ANOVA, a similar parameter for measuring the strength of group comparison is standardized effect size (SES). One issue with SES is that its values are incomparable for contrasts with different coefficients. SMCV does not have such an issue.
 have means
have means  and variances
and variances  , respectively. A contrast variable
, respectively. A contrast variable 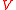 is defined by
is defined by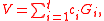
where the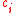 's are a set of coefficients representing a comparison of interest and satisfy
's are a set of coefficients representing a comparison of interest and satisfy 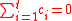 . The SMCV of contrast variable
. The SMCV of contrast variable 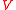 , denoted by
, denoted by  , is defined as
, is defined as
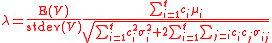
where is the covariance of
is the covariance of 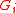 and
and 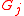 . When
. When 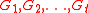 are independent,
are independent,
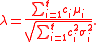
 ) of SMCV can be used to classify the strength of a comparison represented by a contrast variable, as shown in the following table.
) of SMCV can be used to classify the strength of a comparison represented by a contrast variable, as shown in the following table.
This classifying rule has a probabilistic basis due to the link between SMCV and c+-probability
.
Estimation and inference of SMCV for multi-factor experiments has also been discussed.
The estimation of SMCV relies on how samples are obtained in a study. When the groups are correlated, it is usually difficult to estimate the covariance among groups. In such a case, a good strategy is to obtain matched or paired samples (or subjects) and to conduct contrast analysis based on the matched samples. A simple example of matched contrast analysis is the analysis of paired difference of drug effects after and before taking a drug in the same patients. By contrast, another strategy is to not match or pair the samples and to conduct contrast analysis based on the unmatched or unpaired samples. A simple example of unmatched contrast analysis is the comparison of efficacy between a new drug taken by some patients and a standard drug taken by other patients. Methods of estimation for SMCV and c+-probability in matched contrast analysis may differ from those used in unmatched contrast analysis.
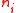 ,
,
from the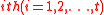 group
group 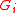 .
.
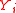 's are independent. Let
's are independent. Let 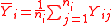 ,
,
and
When the groups have unequal variance, the maximal likelihood estimate (MLE) and method-of-moment estimate (MM) of SMCV (
groups have unequal variance, the maximal likelihood estimate (MLE) and method-of-moment estimate (MM) of SMCV ( ) are, respectively
) are, respectively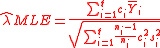
and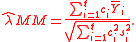
When the groups have equal variance, under normality assumption, the uniformly minimal variance unbiased estimate (UMVUE) of SMCV (
groups have equal variance, under normality assumption, the uniformly minimal variance unbiased estimate (UMVUE) of SMCV ( ) is
) is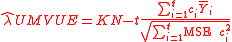
where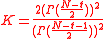 . The confidence interval of SMCV can be made using the following non-central t-distribution:
. The confidence interval of SMCV can be made using the following non-central t-distribution: 
where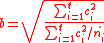
 independent samples
independent samples 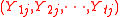 from
from  groups (
groups (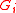 's), where
's), where  . Then
. Then
the observed value of a contrast
observed value of a contrast
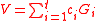 is
is 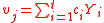 .
.
Let and
and  be the sample mean and sample variance of the contrast variable
be the sample mean and sample variance of the contrast variable  , respectively. Under normality assumptions, the UMVUE
, respectively. Under normality assumptions, the UMVUE
estimate of SMCV is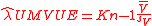
where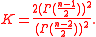
A confidence interval
for SMCV can be made using the following non-central t-distribution:
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the standardized mean of a contrast variable (SMCV or SMC), is a parameter assessing effect size
Effect size
In statistics, an effect size is a measure of the strength of the relationship between two variables in a statistical population, or a sample-based estimate of that quantity...
. The SMCV is defined as mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
divided by the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of a contrast variable
Contrast (statistics)
In statistics, particularly analysis of variance, a contrast is a linear combination of two or more factor level means whose coefficients add up to zero. A simple contrast is the difference between two means...
.
The SMCV was first proposed for one-way ANOVA cases
and was then extended to multi-factor ANOVA cases
.
Background
Consistent interpretations for the strength of group comparison, as represented by a contrast, are important.The standardized mean of a contrast variable, along with c+-probability
C+-probability
In statistics, a c+-probability is the probability that a contrast variable obtains a positive value.Using a replication probability, the c+-probability is defined as follows: if we get a random draw from each group and calculate the sampled value of the contrast variable based on the random...
, can provide a consistent interpretation of the strength of a comparison. When there are only two groups involved in a comparison, SMCV is the same as SSMD. SSMD belongs to a popular type of effect-size measure called "standardized mean differences" which includes Cohen's
 and Glass's
and Glass's 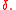
In ANOVA, a similar parameter for measuring the strength of group comparison is standardized effect size (SES). One issue with SES is that its values are incomparable for contrasts with different coefficients. SMCV does not have such an issue.
Concept
Suppose the random values in t groups represented by random variables have means
have means  and variances
and variances  , respectively. A contrast variable
, respectively. A contrast variable 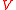 is defined by
is defined by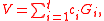
where the
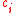 's are a set of coefficients representing a comparison of interest and satisfy
's are a set of coefficients representing a comparison of interest and satisfy 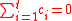 . The SMCV of contrast variable
. The SMCV of contrast variable 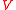 , denoted by
, denoted by  , is defined as
, is defined as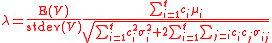
where
 is the covariance of
is the covariance of 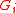 and
and 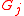 . When
. When 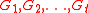 are independent,
are independent,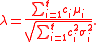
Classifying rule for the strength of group comparisons
The population value (denoted by ) of SMCV can be used to classify the strength of a comparison represented by a contrast variable, as shown in the following table.
) of SMCV can be used to classify the strength of a comparison represented by a contrast variable, as shown in the following table.This classifying rule has a probabilistic basis due to the link between SMCV and c+-probability
C+-probability
In statistics, a c+-probability is the probability that a contrast variable obtains a positive value.Using a replication probability, the c+-probability is defined as follows: if we get a random draw from each group and calculate the sampled value of the contrast variable based on the random...
.
| Effect type | Effect subtype | Thresholds for negative SMCV | Thresholds for positive SMCV |
|---|---|---|---|
| Extra large | Extremely strong |  |
 |
| Very strong |  |
 |
|
| Strong |  |
 |
|
| Fairly strong |  |
 |
|
| Large | Moderate |  |
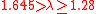 |
| Fairly moderate | 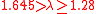 |
 |
|
| Medium | Fairly weak |  |
 |
| Weak |  |
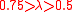 |
|
| Very weak | 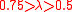 |
 |
|
| Small | Extremely weak |  |
 |
| No effect |  |
||
Statistical estimation and inference
The estimation and inference of SMCV presented below is for one-factor experiments.Estimation and inference of SMCV for multi-factor experiments has also been discussed.
The estimation of SMCV relies on how samples are obtained in a study. When the groups are correlated, it is usually difficult to estimate the covariance among groups. In such a case, a good strategy is to obtain matched or paired samples (or subjects) and to conduct contrast analysis based on the matched samples. A simple example of matched contrast analysis is the analysis of paired difference of drug effects after and before taking a drug in the same patients. By contrast, another strategy is to not match or pair the samples and to conduct contrast analysis based on the unmatched or unpaired samples. A simple example of unmatched contrast analysis is the comparison of efficacy between a new drug taken by some patients and a standard drug taken by other patients. Methods of estimation for SMCV and c+-probability in matched contrast analysis may differ from those used in unmatched contrast analysis.
Unmatched samples
Consider an independent sample of size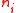 ,
,from the
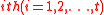 group
group 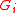 .
.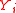 's are independent. Let
's are independent. Let 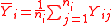 ,
,and
When the
 groups have unequal variance, the maximal likelihood estimate (MLE) and method-of-moment estimate (MM) of SMCV (
groups have unequal variance, the maximal likelihood estimate (MLE) and method-of-moment estimate (MM) of SMCV ( ) are, respectively
) are, respectively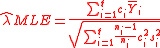
and
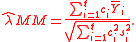
When the
 groups have equal variance, under normality assumption, the uniformly minimal variance unbiased estimate (UMVUE) of SMCV (
groups have equal variance, under normality assumption, the uniformly minimal variance unbiased estimate (UMVUE) of SMCV ( ) is
) is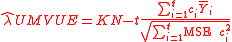
where
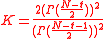 . The confidence interval of SMCV can be made using the following non-central t-distribution:
. The confidence interval of SMCV can be made using the following non-central t-distribution: 
where
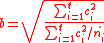
Matched samples
In matched contrast analysis, assume that there are independent samples
independent samples 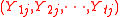 from
from  groups (
groups (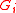 's), where
's), where  . Then
. Thenthe
 observed value of a contrast
observed value of a contrast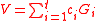 is
is 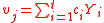 .
.Let
 and
and  be the sample mean and sample variance of the contrast variable
be the sample mean and sample variance of the contrast variable  , respectively. Under normality assumptions, the UMVUE
, respectively. Under normality assumptions, the UMVUEMinimum-variance unbiased estimator
In statistics a uniformly minimum-variance unbiased estimator or minimum-variance unbiased estimator is an unbiased estimator that has lower variance than any other unbiased estimator for all possible values of the parameter.The question of determining the UMVUE, if one exists, for a particular...
estimate of SMCV is
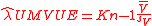
where
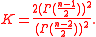
A confidence interval
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
for SMCV can be made using the following non-central t-distribution: