State-merging
Encyclopedia
In quantum information theory, quantum state merging (HOW05.I,HOW05.II) is the transfer of a quantum state when the receiver already has part of the state. The process optimally transfers partial information using entanglement and classical communication. It allows for sending information using an amount of entanglement given by the conditional quantum entropy
,
with 
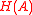the Von Neumann entropy
,
. It thus provides an operational meaning to this quantity.
Unlike its classical counterpart, the quantum conditional entropy can be negative. In this case, the sender can transfer the state to the receiver using no entanglement, and as an added bonus, this amount of entanglement can be gained, rather than used. Thus quantum information can be negative.
The amount of classical information needed is the mutual information
. The case where the classical communication is replaced by quantum communication was considered in (ADHW09). This is known as the Fully Quantum Slepian-Wolf Theorem, since everything is sent down the quantum channel. A single-shot version of state merging was found by Berta (B10), and a multiparty single shot version was found in (DH10). The quantum discord
has been interpreted using state merging (MD10).
Conditional quantum entropy
The conditional quantum entropy is an entropy measure used in quantum information theory. It is a generalization of the conditional entropy of classical information theory...
,
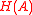with the Von Neumann entropyVon Neumann entropy
In quantum statistical mechanics, von Neumann entropy, named after John von Neumann, is the extension of classical entropy concepts to the field of quantum mechanics....
,
. It thus provides an operational meaning to this quantity.Unlike its classical counterpart, the quantum conditional entropy can be negative. In this case, the sender can transfer the state to the receiver using no entanglement, and as an added bonus, this amount of entanglement can be gained, rather than used. Thus quantum information can be negative.
The amount of classical information needed is the mutual information
. The case where the classical communication is replaced by quantum communication was considered in (ADHW09). This is known as the Fully Quantum Slepian-Wolf Theorem, since everything is sent down the quantum channel. A single-shot version of state merging was found by Berta (B10), and a multiparty single shot version was found in (DH10). The quantum discordQuantum discord
In quantum information theory, quantum discord is a measure of nonclassical correlations between two subsystems of a quantum system. It includes correlations that are due to quantum physical effects but do not necessarily involve quantum entanglement....
has been interpreted using state merging (MD10).